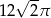Pole równoległoboku 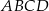 jest równe 120. Na bokach
jest równe 120. Na bokach 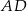 i
i 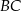 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 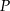 i
i 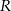 , takie, że
, takie, że 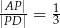 i
i 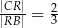 (zobacz rysunek)
(zobacz rysunek)
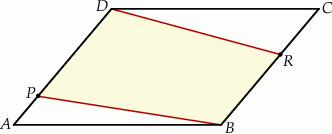
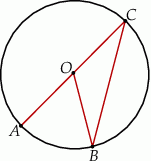
Pole czworokąta  jest równe
jest równe
A) 81 B) 96 C) 102 D) 118
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Pole równoległoboku  jest równe 120. Na bokach
jest równe 120. Na bokach  i
i  wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty  i
i  , takie, że
, takie, że 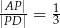 i
i 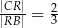 (zobacz rysunek)
(zobacz rysunek)

Pole czworokąta 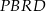 jest równe
jest równe
A) 81 B) 96 C) 102 D) 118
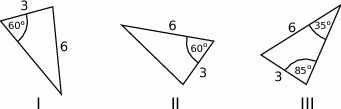
Na rysunkach I, II i III dane są trzy trójkąty.
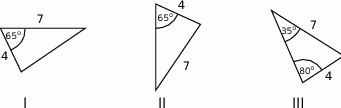
Przystające są trójkąty tylko na rysunkach
A) I i II B) I i III C) II i III D) I, II i III
Na rysunkach I, II i III dane są trzy trójkąty.
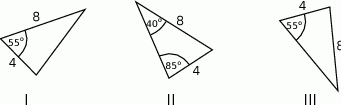
Na których rysunkach trójkąty są przystające?
A) I i II B) I i III C) II i III D) I, II i III
Na rysunkach I, II i III dane są trzy trójkąty.
Przystające są trójkąty tylko na rysunkach
A) I i II B) I i III C) II i III D) I, II i III
W trójkącie  bok
bok  ma długość
ma długość  . Ponadto
. Ponadto 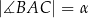 ,
, 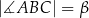 oraz
oraz 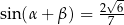 . Długość okręgu opisanego na trójkącie
. Długość okręgu opisanego na trójkącie 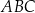 jest równa
jest równa
A) 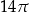 B)
B) 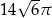 C)
C) 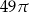 D)
D) 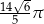
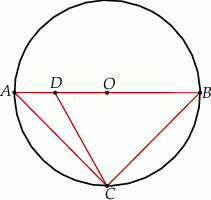
Odcinek 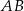 jest średnicą okręgu o środku
jest średnicą okręgu o środku 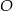 i promieniu
i promieniu  , a punkt
, a punkt 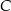 jest środkiem łuku o końcach
jest środkiem łuku o końcach 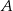 i
i 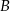 (zobacz rysunek). Na odcinku
(zobacz rysunek). Na odcinku 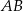 wybrano punkt
wybrano punkt 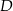 taki, że
taki, że 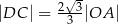 .
.
Pole trójkąta 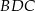 jest równe
jest równe
A) 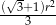 B)
B) 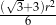 C)
C) 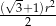 D)
D) 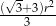
W trójkącie 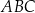 długość boku
długość boku 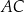 jest równa 3, a długość boku
jest równa 3, a długość boku 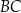 jest równa 4. Dwusieczna kąta
jest równa 4. Dwusieczna kąta 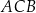 przecina bok
przecina bok 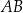 w punkcie
w punkcie 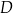 . Stosunek
. Stosunek 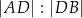 jest równy
jest równy
A) 4 : 3 B) 4 : 7 C) 3 : 4 D) 3 : 7
W trójkącie 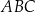 długość boku
długość boku 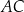 jest równa 6, a długość boku
jest równa 6, a długość boku 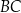 jest równa 8. Dwusieczna kąta
jest równa 8. Dwusieczna kąta 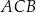 przecina bok
przecina bok 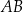 w punkcie
w punkcie 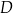 . Stosunek
. Stosunek 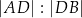 jest równy
jest równy
A) 4 : 3 B) 3 : 4 C) 4 : 7 D) 3 : 7
Punkt  jest środkiem okręgu o średnicy
jest środkiem okręgu o średnicy  (tak jak na rysunku). Kąt
(tak jak na rysunku). Kąt  ma miarę
ma miarę
A) 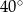 B)
B) 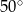 C)
C) 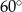 D)
D) 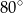
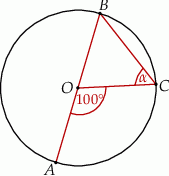
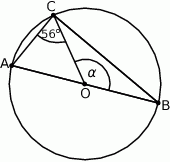
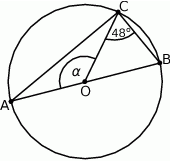
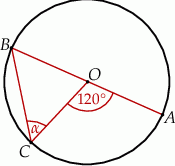
W okręgu o środku 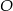 dany jest kąt wpisany
dany jest kąt wpisany  o mierze
o mierze 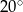 (patrz rysunek).
(patrz rysunek).
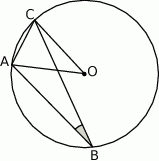
Miara kąta  jest równa
jest równa
A) 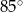 B)
B) 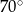 C)
C) 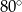 D)
D) 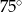
Na okręgu o środku w punkcie  leżą punkty
leżą punkty  (zobacz rysunek).
(zobacz rysunek).
Odcinek 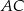 jest średnicą okręgu. Kąt
jest średnicą okręgu. Kąt 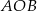 ma miarę
ma miarę 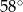 . Kąt
. Kąt 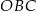 ma miarę równą
ma miarę równą
A) 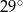 B)
B) 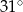 C)
C) 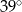 D)
D) 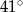
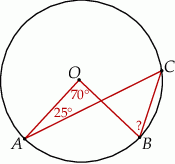
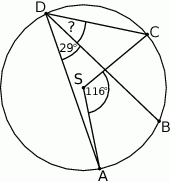
Na okręgu o środku w punkcie  wybrano trzy punkty
wybrano trzy punkty 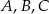 tak, że
tak, że 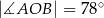 ,
, 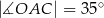 . Cięciwa
. Cięciwa 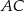 przecina promień
przecina promień 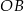 (zobacz rysunek). Wtedy miara
(zobacz rysunek). Wtedy miara  jest równa
jest równa
A)  B)
B) 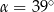 C)
C) 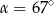 D)
D) 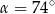
Na okręgu o środku w punkcie 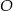 leżą punkty
leżą punkty 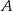 ,
, 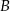 oraz
oraz 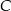 . Odcinek
. Odcinek 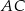 jest średnicą tego okręgu, a kąt środkowy
jest średnicą tego okręgu, a kąt środkowy 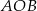 ma miarę
ma miarę 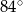 (zobacz rysunek).
(zobacz rysunek).
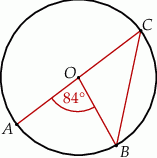
Miara kąta 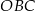 jest równa
jest równa
A) 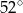 B)
B) 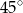 C)
C) 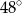 D)
D) 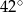
Odcinek  jest średnicą okręgu o środku
jest średnicą okręgu o środku  (rysunek).
(rysunek).
Miara kąta  jest równa
jest równa
A) 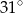 B)
B) 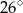 C)
C) 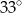 D)
D) 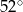
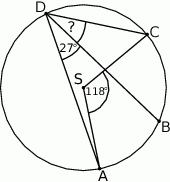
Na okręgu o środku w punkcie 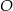 wybrano trzy punkty
wybrano trzy punkty 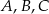 tak, że
tak, że 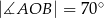 ,
, 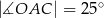 . Cięciwa
. Cięciwa 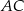 przecina promień
przecina promień 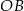 (zobacz rysunek). Wtedy miara
(zobacz rysunek). Wtedy miara 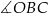 jest równa
jest równa
A) 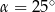 B)
B) 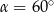 C)
C) 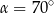 D)
D) 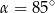
Na okręgu o środku w punkcie 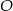 leży punkt
leży punkt 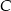 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 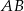 jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy
jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy  ma miarę
ma miarę
A) 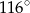 B)
B) 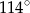 C)
C) 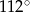 D)
D) 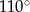
Na okręgu o środku w punkcie 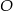 leży punkt
leży punkt 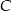 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek  jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy
jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy  ma miarę
ma miarę
A) 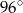 B)
B) 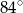 C)
C) 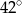 D)
D) 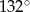
W okręgu o środku 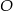 dany jest kąt wpisany
dany jest kąt wpisany  o mierze
o mierze 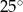 (patrz rysunek).
(patrz rysunek).
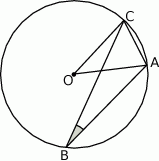
Miara kąta  jest równa
jest równa
A) 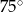 B)
B) 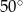 C)
C) 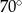 D)
D) 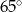
Punkt  jest środkiem okręgu o średnicy
jest środkiem okręgu o średnicy  (tak jak na rysunku). Kąt
(tak jak na rysunku). Kąt  ma miarę
ma miarę
A) 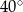 B)
B) 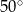 C)
C) 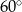 D)
D) 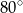
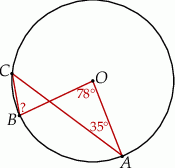
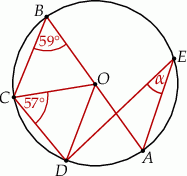
Na okręgu o środku w punkcie 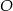 leżą punkty
leżą punkty 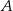 ,
, 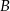 oraz
oraz 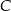 . Odcinek
. Odcinek 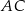 jest średnicą tego okręgu, a kąt środkowy
jest średnicą tego okręgu, a kąt środkowy 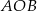 ma miarę
ma miarę  (zobacz rysunek).
(zobacz rysunek).
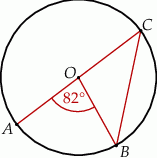
Miara kąta  jest równa
jest równa
A) 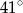 B)
B) 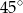 C)
C) 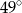 D)
D) 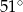
Na okręgu o środku w punkcie  leżą punkty
leżą punkty  (zobacz rysunek).
(zobacz rysunek).
Odcinek 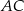 jest średnicą okręgu. Kąt
jest średnicą okręgu. Kąt 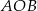 ma miarę
ma miarę 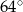 . Kąt
. Kąt 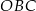 ma miarę równą
ma miarę równą
A) 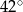 B)
B) 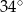 C)
C) 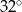 D)
D) 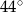
Bok rombu tworzy z krótszą przekątną kąt o mierze 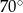 . Kąt ostry tego rombu ma miarę
. Kąt ostry tego rombu ma miarę
A) 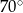 B)
B) 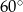 C)
C) 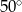 D)
D) 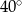
Bok rombu tworzy z krótszą przekątną kąt o mierze 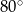 . Kąt ostry tego rombu ma miarę
. Kąt ostry tego rombu ma miarę
A) 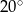 B)
B) 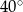 C)
C) 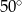 D)
D) 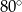
Zaznaczony na rysunku kąt  jest równy
jest równy
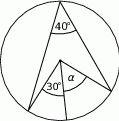
A) 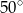 B)
B) 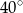 C)
C) 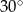 D)
D) 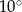
Punkty 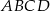 leżą na okręgu o środku
leżą na okręgu o środku 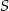 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta  jest równa
jest równa
A) 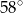 B)
B) 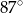 C)
C) 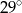 D)
D) 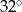
Punkty 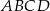 leżą na okręgu o środku
leżą na okręgu o środku 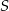 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta  jest równa
jest równa
A) 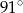 B)
B) 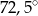 C)
C) 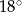 D)
D) 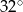
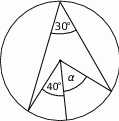
Zaznaczony na rysunku kąt  jest równy
jest równy
A) 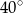 B)
B) 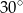 C)
C) 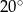 D)
D) 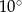
Wysokości 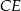 i
i 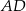 trójkąta równoramiennego
trójkąta równoramiennego 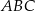 przecinają się w punkcie
przecinają się w punkcie 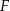 . Podstawa trójkąta
. Podstawa trójkąta 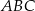 ma długość 13, a jego obwód jest równy 65.
ma długość 13, a jego obwód jest równy 65.
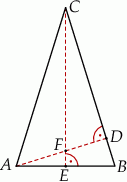
Stosunek pola trójkąta 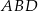 do pola trójkąta
do pola trójkąta 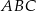 jest równy
jest równy
A)  B)
B) 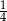 C)
C) 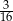 D)
D) 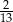
Obwód trójkąta prostokątnego 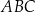 jest równy
jest równy 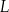 . Na boku
. Na boku 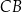 tego trójkąta obrano punkt
tego trójkąta obrano punkt 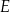 , a na boku
, a na boku 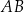 obrano punkt
obrano punkt 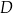 tak, że
tak, że 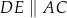 oraz
oraz 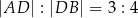 (zobacz rysunek).
(zobacz rysunek).

Obwód trójkąta 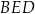 jest równy
jest równy
A) 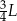 B)
B) 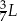 C)
C) 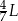 D)
D) 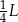
Miary kątów wewnętrznych pewnego pięciokąta pozostają w stosunku 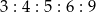 . Najmniejszy kąt wewnętrzny tego pięciokąta ma miarę
. Najmniejszy kąt wewnętrzny tego pięciokąta ma miarę
A) 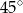 B)
B) 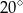 C)
C) 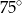 D)
D) 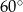
Miary kątów wewnętrznych pewnego pięciokąta pozostają w stosunku 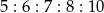 . Najmniejszy kąt wewnętrzny tego pięciokąta ma miarę
. Najmniejszy kąt wewnętrzny tego pięciokąta ma miarę
A) 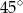 B)
B) 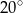 C)
C) 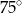 D)
D) 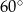
W trójkącie równoramiennym 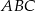 wysokość ma długość 8, a długość podstawy
wysokość ma długość 8, a długość podstawy 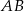 stanowi
stanowi 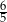 długości ramienia. Podstawa tego trójkąta ma długość
długości ramienia. Podstawa tego trójkąta ma długość
A) 30 B) 6 C) 12 D) 10
Miara kąta  pod jakim przecinają się styczne do okręgu o środku
pod jakim przecinają się styczne do okręgu o środku 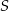 wynosi
wynosi
A)  B)
B)  C)
C) 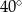 D)
D) 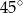
Punkty 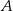 oraz
oraz 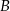 leżą na okręgu o środku
leżą na okręgu o środku 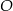 . Proste
. Proste 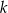 i
i 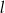 są styczne do tego okręgu w punktach – odpowiednio –
są styczne do tego okręgu w punktach – odpowiednio – 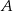 i
i 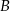 . Te proste przecinają się w punkcie
. Te proste przecinają się w punkcie 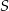 i tworzą kąt o mierze
i tworzą kąt o mierze 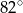 (zobacz rysunek).
(zobacz rysunek).
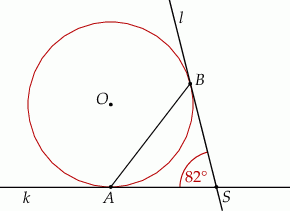
Miara kąta 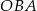 jest równa
jest równa
A) 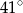 B)
B) 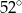 C)
C) 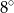 D)
D) 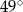
Przez punkty 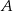 i
i 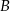 , leżące na okręgu o środku
, leżące na okręgu o środku 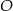 , poprowadzono proste styczne do tego okręgu, przecinające się w punkcie
, poprowadzono proste styczne do tego okręgu, przecinające się w punkcie 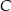 (zobacz rysunek).
(zobacz rysunek).
Miara kąta  jest równa
jest równa
A)  B)
B) 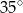 C)
C) 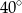 D)
D) 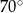
Do okręgu o środku 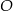 poprowadzono z zewnętrznego punktu
poprowadzono z zewnętrznego punktu 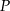 dwie styczne przecinające się w
dwie styczne przecinające się w 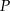 pod kątem
pod kątem 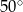 (zobacz rysunek). Punktami styczności są, odpowiednio, punkty
(zobacz rysunek). Punktami styczności są, odpowiednio, punkty 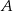 i
i  .
.
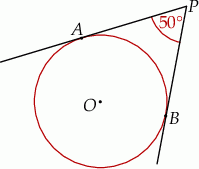
Kąt  ma miarę
ma miarę
A)  B)
B) 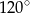 C)
C) 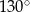 D)
D) 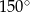
Punkty 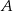 oraz
oraz 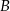 leżą na okręgu o środku
leżą na okręgu o środku 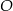 . Proste
. Proste 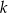 i
i 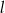 są styczne do tego okręgu w punktach – odpowiednio –
są styczne do tego okręgu w punktach – odpowiednio – 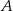 i
i 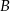 . Te proste przecinają się w punkcie
. Te proste przecinają się w punkcie 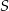 i tworzą kąt o mierze
i tworzą kąt o mierze 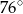 (zobacz rysunek).
(zobacz rysunek).
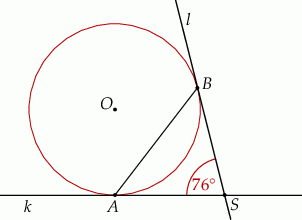
Miara kąta  jest równa
jest równa
A)  B)
B)  C)
C) 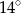 D)
D) 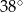
Długość boku 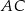 w trójkącie przedstawionym na poniższym rysunku jest równa
w trójkącie przedstawionym na poniższym rysunku jest równa
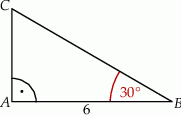
A) 3 B) 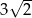 C)
C) 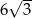 D)
D) 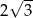
Przekątne dzielą równoległobok na cztery trójkąty
A) przystające B) podobne C) o równych polach D) o równych obwodach
Długość boku trójkąta równobocznego jest równa 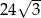 . Promień okręgu wpisanego w ten trójkąt jest równy
. Promień okręgu wpisanego w ten trójkąt jest równy
A) 36 B) 18 C) 12 D) 6
Długość boku trójkąta równobocznego jest równa 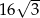 . Promień okręgu wpisanego w ten trójkąt jest równy
. Promień okręgu wpisanego w ten trójkąt jest równy
A) 4 B) 8 C) 12 D) 24
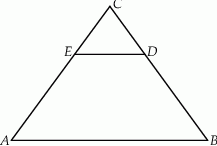
W trójkącie 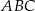 punkt
punkt 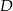 leży na boku
leży na boku 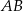 , punkt
, punkt 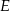 leży na boku
leży na boku 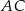 , a ponadto odcinek
, a ponadto odcinek 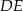 jest równoległy do boku
jest równoległy do boku 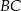 i
i 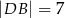 . Pole trójkąta
. Pole trójkąta  jest równe 12, a pole trapezu
jest równe 12, a pole trapezu  jest równe 15 (zobacz rysunek).
jest równe 15 (zobacz rysunek).
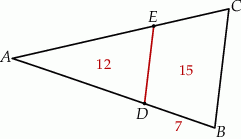
Odcinek 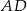 ma długość
ma długość
A) 5,6 B) 12 C) 14 D) 9
Podstawa trójkąta równoramiennego 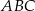 ma długość 19. Na ramionach
ma długość 19. Na ramionach 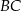 i
i 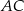 wybrano punkty
wybrano punkty 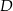 i
i 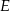 odpowiednio tak, że
odpowiednio tak, że 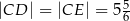 oraz
oraz 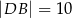 .
.
Odległość między prostymi  i
i  jest równa
jest równa
A) 5 B) 8 C) 10 D) 12
W trapezie  (
(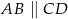 ) dłuższa podstawa ma długość
) dłuższa podstawa ma długość 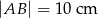 . Odcinek łączący środki ramion w tym trapezie ma długość 7 cm. Długość krótszej podstawy wynosi
. Odcinek łączący środki ramion w tym trapezie ma długość 7 cm. Długość krótszej podstawy wynosi
A) 5 cm B) 7 cm C) 4 cm D) 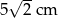
Pole koła przedstawionego na rysunku jest równe
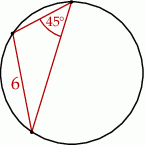
A) 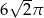 B)
B) 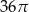 C)
C) 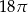 D)
D)