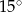W trapezie 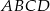 (
(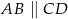 ) dłuższa podstawa ma długość
) dłuższa podstawa ma długość 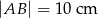 . Odcinek łączący środki ramion w tym trapezie ma długość 7 cm. Długość krótszej podstawy wynosi
. Odcinek łączący środki ramion w tym trapezie ma długość 7 cm. Długość krótszej podstawy wynosi
A) 5 cm B) 7 cm C) 4 cm D) 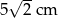
/Szkoła średnia/Zadania testowe/Geometria/Planimetria
Pole koła przedstawionego na rysunku jest równe
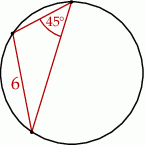
A) 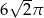 B)
B) 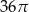 C)
C) 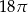 D)
D) 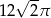
Punkty 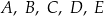 leżą na okręgu o środku
leżą na okręgu o środku 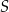 . Miara kąta
. Miara kąta 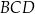 jest równa
jest równa 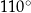 , a miara kąta
, a miara kąta 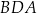 jest równa
jest równa 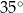 (zobacz rysunek).
(zobacz rysunek).

Wtedy kąt 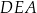 ma miarę równą
ma miarę równą
A) 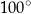 B)
B) 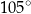 C)
C) 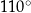 D)
D) 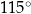
Jedna z przyprostokątnych w trójkącie prostokątnym ma długość 3 cm, a przeciwprostokątna 4 cm. Najmniejszym kątem tego trójkąta jest  . Wartość wyrażenia
. Wartość wyrażenia 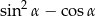 wynosi
wynosi
A) 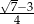 B)
B) 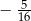 C)
C) 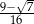 D) 1
D) 1
Trójkąt, w którym stosunek długości boków jest równy 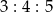 , jest
, jest
A) równoboczny B) prostokątny C) ostrokątny D) rozwartokątny
Boki trójkąta mają długości 20 i 12, a kąt między tymi bokami ma miarę 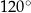 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 60 B) 120 C) 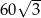 D)
D) 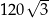
Pole trójkąta o bokach długości 8 oraz 15 i kącie między nimi o mierze 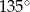 jest równe
jest równe
A) 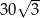 B)
B) 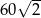 C)
C) 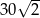 D)
D) 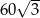
Boki trójkąta mają długości 30 i 8, a kąt między tymi bokami ma miarę 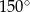 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 60 B) 120 C) 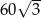 D)
D) 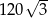
Jaką miarę ma kąt  ?
?
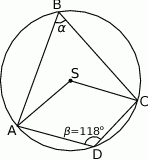
A) 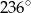 B)
B) 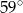 C)
C) 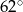 D)
D) 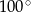
Jaką miarę ma kąt  ?
?
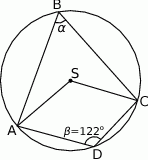
A) 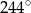 B)
B) 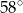 C)
C) 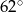 D)
D) 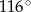
Bok rombu ma długość równą 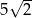 . Przekątne tego rombu nie mogą mieć długości
. Przekątne tego rombu nie mogą mieć długości
A) 14 i 2 B) 10 i 10 C) 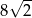 i
i 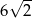 D)
D) 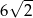 i
i 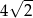
Krótszy bok prostokąta ma długość 6. Kąt między przekątną prostokąta i dłuższym bokiem ma miarę 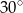 . Dłuższy bok prostokąta ma długość
. Dłuższy bok prostokąta ma długość
A) 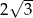 B)
B) 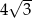 C)
C) 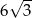 D) 12
D) 12
Dłuższy bok prostokąta ma długość 6. Kąt między przekątną prostokąta i dłuższym bokiem ma miarę 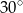 . Krótszy bok prostokąta ma długość
. Krótszy bok prostokąta ma długość
A) 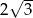 B)
B) 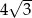 C)
C) 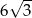 D) 12
D) 12
Odległości punktu 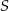 przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków
przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków 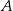 i
i 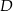 są równe
są równe 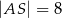 i
i 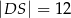 . Bok
. Bok 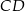 tego czworokąta ma długość
tego czworokąta ma długość
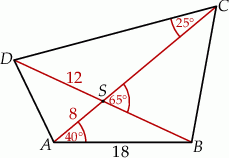
A) 27 B) 16 C) 24 D) 30
Naprzeciwko boków 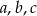 trójkąta
trójkąta 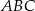 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 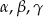 . Wiadomo, że
. Wiadomo, że 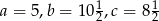 . Wówczas
. Wówczas
A) 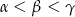 B)
B) 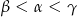 C)
C) 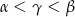 D)
D) 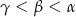
Naprzeciwko boków 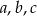 trójkąta
trójkąta 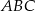 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 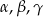 . Wiadomo, że
. Wiadomo, że 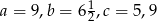 . Wówczas
. Wówczas
A) 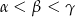 B)
B) 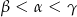 C)
C) 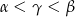 D)
D) 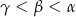
Naprzeciwko boków 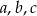 trójkąta
trójkąta 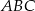 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 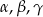 . Wiadomo, że
. Wiadomo, że 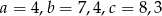 . Wówczas
. Wówczas
A) 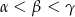 B)
B) 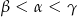 C)
C) 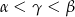 D)
D) 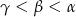
Miary kątów trójkąta pozostają w stosunku 4:5:6. Miary kątów tego trójkąta są równe
A) 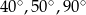 B)
B) 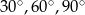 C)
C) 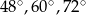 D)
D) 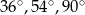
Punkty 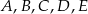 leżą na okręgu o środku
leżą na okręgu o środku 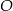 , przy czym
, przy czym 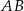 jest średnicą tego okręgu,
jest średnicą tego okręgu, 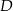 jest środkiem łuku
jest środkiem łuku 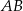 oraz
oraz 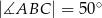 .
.
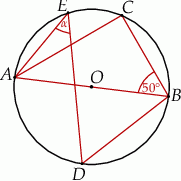
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 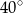 B)
B) 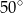 C)
C) 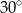 D)
D) 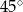
Pole rombu o obwodzie 8 jest równe 1. Kąt ostry tego rombu ma miarę  . Wtedy
. Wtedy
A) 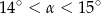 B)
B) 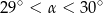 C)
C) 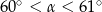 D)
D) 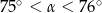
Pole rombu o obwodzie 40 jest równe 35. Kąt ostry tego rombu ma miarę  . Wtedy
. Wtedy
A) 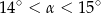 B)
B) 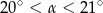 C)
C) 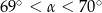 D)
D) 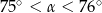
W równoległoboku 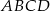 dłuższa podstawa ma długość
dłuższa podstawa ma długość 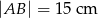 . Wysokości tego równoległoboku mają długości:
. Wysokości tego równoległoboku mają długości: 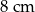 i
i 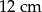 . Zatem krótsza podstawa równoległoboku ma długość
. Zatem krótsza podstawa równoległoboku ma długość
A) 20 cm B) 10 cm C) 3,2 cm D) 1,6 cm
W trójkącie prostokątnym długości przyprostokątnych wynoszą 6 i 8. Stosunek długości odcinków, na które wysokość podzieliła przeciwprostokątną wynosi
A)  B)
B)  C)
C) 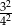 D)
D) 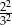
Dany jest trójkąt prostokątny o przyprostokątnych 5 i 12. Poprowadzono wysokość na przeciwprostokątną. Wysokość ta podzieliła przeciwprostokątną na odcinki w stosunku
A) 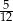 B)
B) 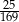 C)
C) 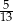 D)
D) 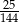
Liczba przekątnych siedmiokąta foremnego jest równa
A) 7 B) 14 C) 21 D) 28
Liczba przekątnych sześciokąta foremnego jest równa
A) 9 B) 14 C) 18 D) 6
Trójkąt można zbudować z odcinków o długościach:
A) 10, 6, 5 B) 4, 2, 1 C) 8, 5, 3 D) 6, 6, 13
Trójkąt można zbudować z odcinków o długościach:
A) 4, 2, 2 B) 7, 4, 3 C) 5, 6, 12 D) 8, 4, 5
Jeśli 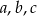 są długościami odcinków, to istnieje trójkąt o bokach
są długościami odcinków, to istnieje trójkąt o bokach 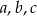 , jeżeli
, jeżeli
A) 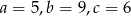
B) 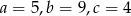
C) 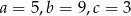
D) 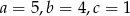
Można zbudować trójkąt z odcinków 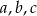 jeśli
jeśli
A) 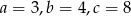
B) 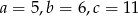
C) 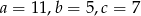
D) 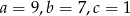
Długościami boków trójkąta mogą być odcinki:
A) 5 cm, 8 cm, 2 cm B) 9 cm, 4 cm, 4 cm C) 3 cm, 2 cm, 1 cm D) 7 cm, 9 cm, 10 cm
O ile 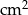 zwiększy się pole prostokąta o wymiarach
zwiększy się pole prostokąta o wymiarach  cm i
cm i 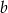 cm, jeżeli bok długości
cm, jeżeli bok długości  cm zwiększymy 2 razy, a bok długości
cm zwiększymy 2 razy, a bok długości 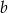 cm zwiększymy o 20%?
cm zwiększymy o 20%?
A) 2,4 B) 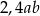 C)
C) 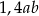 D) 1,4
D) 1,4
O ile 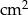 zwiększy się pole prostokąta o wymiarach
zwiększy się pole prostokąta o wymiarach 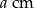 i
i 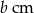 , jeżeli bok długości
, jeżeli bok długości  cm zwiększymy o 130%, a bok długości
cm zwiększymy o 130%, a bok długości 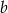 cm zwiększymy o 20%?
cm zwiększymy o 20%?
A) 2,76 B) 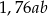 C)
C) 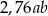 D) 1,76
D) 1,76
O ile 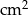 zwiększy się pole prostokąta o wymiarach
zwiększy się pole prostokąta o wymiarach 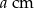 i
i 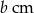 , jeżeli bok długości
, jeżeli bok długości 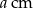 zwiększymy o 100%, a bok długości
zwiększymy o 100%, a bok długości 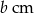 zwiększymy o 20%?
zwiększymy o 20%?
A) 2,4 B) 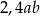 C)
C) 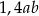 D) 1,4
D) 1,4
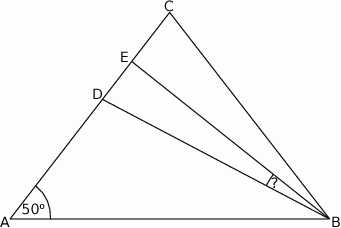
W trójkącie równoramiennym 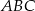 spełnione są warunki:
spełnione są warunki: 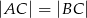 ,
, 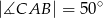 . Odcinek
. Odcinek 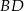 jest dwusieczną kąta
jest dwusieczną kąta 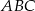 , a odcinek
, a odcinek 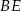 jest wysokością opuszczoną z wierzchołka
jest wysokością opuszczoną z wierzchołka 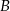 na bok
na bok 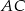 . Miara kąta
. Miara kąta 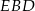 jest równa
jest równa
A) 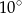 B)
B) 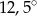 C)
C) 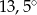 D)
D)