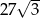Na rysunku przedstawiono okrąg o środku 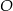 , który jest wpisany w trójkąt
, który jest wpisany w trójkąt 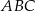 .
.
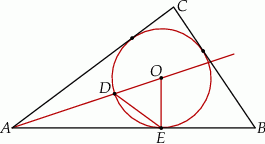
Okrąg ten przecina bok 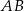 w punkcie
w punkcie 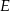 , a odcinek
, a odcinek 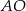 w punkcie
w punkcie 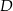 . Jeżeli
. Jeżeli 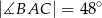 , to miara kąta
, to miara kąta 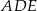 jest równa
jest równa
A) 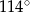 B)
B) 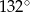 C)
C) 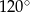 D)
D) 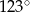
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono okrąg o środku 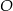 , który jest wpisany w trójkąt
, który jest wpisany w trójkąt 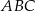 .
.

Okrąg ten przecina bok 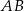 w punkcie
w punkcie 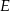 , a odcinek
, a odcinek 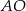 w punkcie
w punkcie 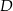 . Jeżeli
. Jeżeli 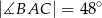 , to miara kąta
, to miara kąta 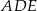 jest równa
jest równa
A) 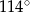 B)
B) 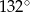 C)
C) 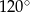 D)
D) 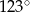
W trójkącie 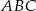 na rysunku obok dane są:
na rysunku obok dane są: 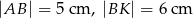 oraz
oraz 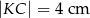 . Wiadomo, że
. Wiadomo, że 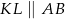 .
.
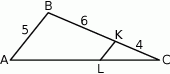
Wówczas:
A) 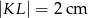 B)
B) 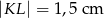 C)
C) 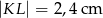 D)
D) 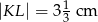
W trójkącie 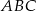 punkt
punkt 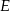 leży na boku
leży na boku 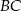 , a punkt
, a punkt 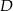 leży na boku
leży na boku 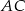 . Odcinek
. Odcinek 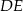 jest równoległy do boku
jest równoległy do boku 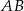 , a ponadto
, a ponadto 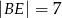 ,
, 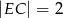 i
i 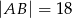 (zobacz rysunek).
(zobacz rysunek).
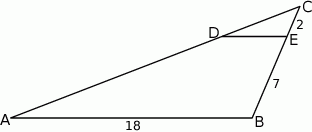
Długość odcinka 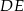 jest równa
jest równa
A) 5 B) 3 C) 6 D) 4
W trójkącie 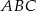 punkt
punkt 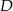 leży na boku
leży na boku 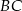 , a punkt
, a punkt 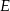 leży na boku
leży na boku 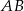 . Odcinek
. Odcinek 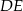 jest równoległy do boku
jest równoległy do boku 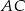 , a ponadto
, a ponadto  ,
, 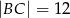 i
i 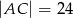 (zobacz rysunek).
(zobacz rysunek).
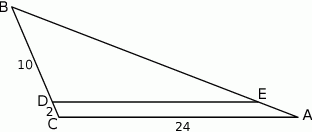
Długość odcinka 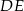 jest równa
jest równa
A) 22 B) 20 C) 12 D) 11
Na rysunku prosta 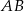 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 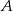 . Punkt
. Punkt  jest środkiem okręgu.
jest środkiem okręgu.
Kąt dopisany  ma miarę:
ma miarę:
A) 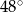 B)
B) 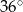 C)
C) 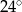 D)
D) 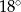
Na rysunku prosta 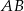 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 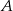 . Punkt
. Punkt  jest środkiem okręgu.
jest środkiem okręgu.
Kąt dopisany  ma miarę:
ma miarę:
A) 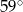 B)
B) 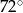 C)
C) 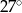 D)
D) 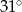
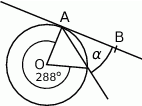
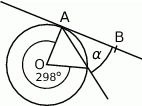
Na rysunku przedstawiono okrąg o środku 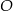 oraz kąt środkowy o mierze
oraz kąt środkowy o mierze 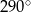 . Punkty
. Punkty 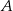 i
i 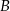 znajdują się na okręgu. Prosta
znajdują się na okręgu. Prosta 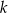 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 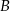 .
.
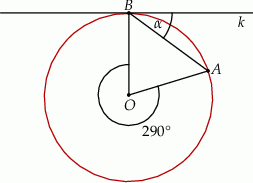
Miara kąta  jest równa
jest równa
A) 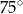 B)
B) 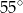 C)
C) 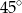 D)
D) 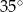
Na rysunku przedstawiono okrąg o środku 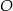 oraz kąt środkowy o mierze
oraz kąt środkowy o mierze 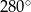 . Punkty
. Punkty 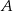 i
i 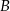 znajdują się na okręgu. Prosta
znajdują się na okręgu. Prosta 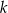 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 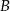 .
.
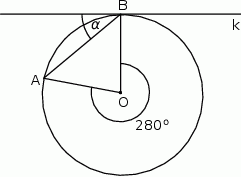
Miara kąta  jest równa
jest równa
A) 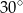 B)
B) 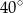 C)
C) 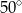 D)
D) 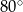
Na rysunku prosta 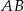 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 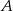 . Punkt
. Punkt 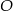 jest środkiem okręgu.
jest środkiem okręgu.
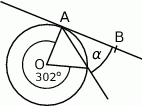
Kąt dopisany  ma miarę:
ma miarę:
A) 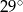 B)
B) 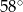 C)
C) 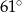 D)
D) 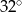
Prosta jest styczna do okręgu. Kąt  (patrz rysunek) ma miarę:
(patrz rysunek) ma miarę:
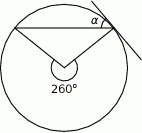
A) 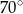 B)
B) 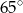 C)
C) 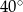 D)
D) 
W trójkącie równobocznym długość każdego boku zmniejszono o 20%. Wtedy pole tego trójkąta
A) zmniejszy się o 20% B) zmniejszy się o 40%
C) zmniejszy się o mniej niż 20% D) zmniejszy się o 36%
Kąt  jest najmniejszym z kątów trójkąta prostokątnego o bokach długości
jest najmniejszym z kątów trójkąta prostokątnego o bokach długości 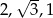 . Wtedy
. Wtedy
A) 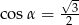 B)
B) 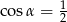 C)
C) 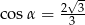 D)
D) 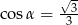
Kąt  jest najmniejszym z kątów trójkąta prostokątnego o bokach długości
jest najmniejszym z kątów trójkąta prostokątnego o bokach długości 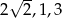 . Wtedy
. Wtedy
A) 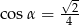 B)
B) 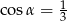 C)
C) 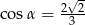 D)
D) 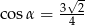
W trójkącie prostokątnym dwa dłuższe boki mają długości 5 i 7. Obwód tego trójkąta jest równy
A) 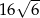 B)
B) 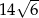 C)
C) 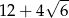 D)
D) 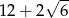
Dwa dłuższe boki trójkąta prostokątnego mają długości 3 cm oraz 4 cm. Długość najkrótszego boku tego trójkąta wynosi
A) 5 cm B) 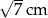 C) 2,6 cm D)
C) 2,6 cm D) 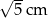
W trójkącie prostokątnym dwa dłuższe boki mają długości 7 i 9. Obwód tego trójkąta jest równy
A) 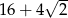 B)
B) 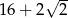 C)
C) 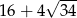 D)
D) 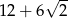
Dany jest trójkąt, którego kąty mają miary 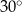 ,
, 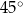 oraz
oraz 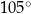 . Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –
. Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –  ,
, 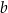 oraz
oraz  (zobacz rysunek).
(zobacz rysunek).

Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F. Pole tego trójkąta poprawnie określa wyrażenie
A) 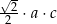 B)
B) 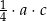 C)
C) 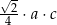
D) 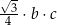 E)
E) 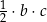 F)
F) 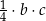
Dany jest trójkąt, którego kąty mają miary 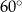 ,
, 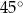 oraz
oraz 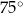 . Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –
. Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –  ,
, 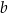 oraz
oraz  (zobacz rysunek).
(zobacz rysunek).
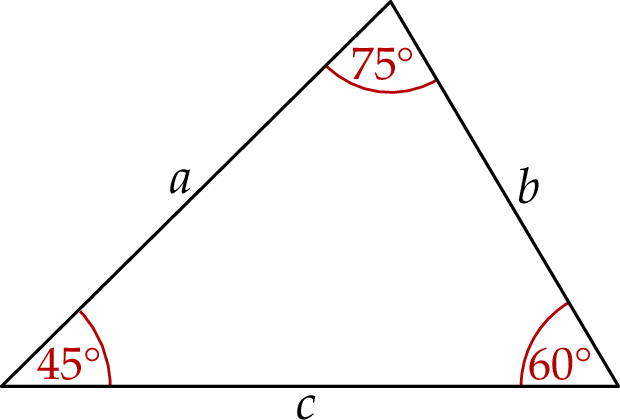
Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F. Pole tego trójkąta poprawnie określa wyrażenie
A) 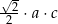 B)
B) 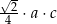 C)
C) 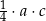
D) 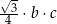 E)
E) 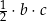 F)
F) 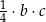
Niech  i
i 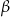 oznaczają miary kątów ostrych w dowolnym trójkącie prostokątnym. Wówczas zachodzi równość:
oznaczają miary kątów ostrych w dowolnym trójkącie prostokątnym. Wówczas zachodzi równość:
A) 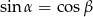 B)
B) 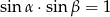 C)
C) 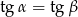 D)
D) 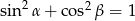
Przekątna 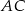 prostokąta
prostokąta 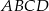 ma długość
ma długość 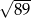 , a bok
, a bok 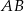 jest o 3 dłuższy od boku
jest o 3 dłuższy od boku 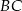 . Oblicz pole prostokąta.
. Oblicz pole prostokąta.
A) 8 B) 40 C) 5 D) 20
Jeden z boków równoległoboku ma długość równą 5. Przekątne tego równoległoboku mogą mieć długości
A) 4 i 6 B) 4 i 3 C) 10 i 10 D) 5 i 5
Jeden z boków równoległoboku ma długość równą 12. Przekątne tego równoległoboku mogą mieć długości
A) 10 i 10 B) 18 i 6 C) 12 i 12 D) 30 i 30
Przekątna kwadratu 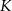 ma długość 2, a obwód kwadratu
ma długość 2, a obwód kwadratu 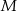 ma długość 16. Skala podobieństwa kwadratu
ma długość 16. Skala podobieństwa kwadratu 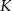 do kwadratu
do kwadratu 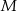 jest równa:
jest równa:
A) 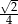 B)
B) 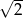 C) 4 D)
C) 4 D) 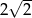
Dany jest sześciokąt foremny 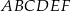 o polu równym
o polu równym 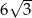 (zobacz rysunek).
(zobacz rysunek).
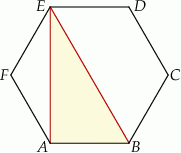
Długość odcinka 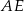 jest równa
jest równa
A) 2 B) 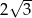 C)
C) 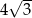 D) 4
D) 4
Długości boków trójkąta są liczbami całkowitymi. Jeden bok ma 7 cm, a drugi ma 2 cm. Trzeci bok tego trójkąta może mieć długość
A) 12 cm B) 9 cm C) 6 cm D) 3 cm
Długości boków trójkąta są liczbami całkowitymi. Jeden bok ma 4 cm, a drugi ma 9 cm. Trzeci bok tego trójkąta może mieć długość
A) 4 cm B) 5 cm C) 14 cm D) 9 cm
Punkty 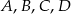 leżą na okręgu w podanej kolejności. Cięciwy
leżą na okręgu w podanej kolejności. Cięciwy 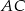 i
i 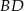 przecinają się w punkcie
przecinają się w punkcie 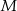 . Zatem
. Zatem
A) 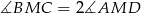 B)
B) 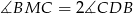 C)
C) 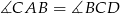 D)
D) 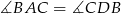
Punkty 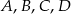 leżą na okręgu w podanej kolejności. Cięciwy
leżą na okręgu w podanej kolejności. Cięciwy 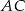 i
i 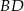 przecinają się w punkcie
przecinają się w punkcie 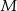 . Zatem
. Zatem
A) 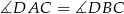 B)
B) 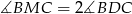 C)
C) 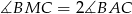 D)
D) 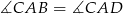
Punkty 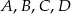 leżą na okręgu w podanej kolejności. Cięciwy
leżą na okręgu w podanej kolejności. Cięciwy 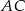 i
i 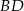 przecinają się w punkcie
przecinają się w punkcie 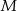 . Zatem
. Zatem
A) 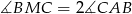 B)
B) 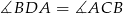 C)
C) 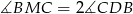 D)
D) 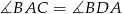
Punkty 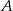 ,
, 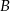 i
i 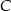 leżą na okręgu o środku
leżą na okręgu o środku 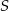 , a prosta
, a prosta 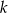 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 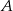 .
.
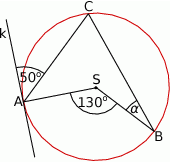
Zaznaczony na rysunku kąt  zawarty między promieniem
zawarty między promieniem 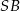 i cięciwą
i cięciwą 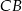 ma miarę
ma miarę
A) 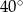 B)
B) 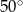 C)
C) 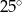 D)
D) 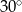
Jeżeli trójkąty 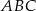 i
i 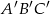 są podobne, a ich obwody są odpowiednio równe 25 cm i 50 cm, to skala podobieństwa trójkątów
są podobne, a ich obwody są odpowiednio równe 25 cm i 50 cm, to skala podobieństwa trójkątów 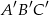 i
i 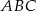 jest równa
jest równa
A) 2 B) 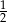 C)
C) 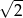 D)
D) 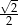
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 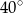 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 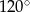 B)
B) 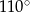 C)
C) 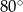 D)
D) 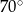
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 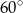 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 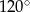 B)
B) 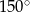 C)
C) 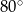 D)
D) 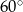
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 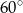 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 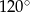 B)
B) 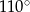 C)
C) 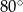 D)
D) 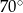
Pole równoległoboku o bokach długości 6 i 8 oraz kącie rozwartym 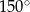 jest równe
jest równe
A) 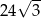 B) 48 C)
B) 48 C) 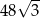 D) 24
D) 24
Dany jest równoległobok o bokach długości 3 i 4 oraz o kącie między nimi o mierze 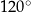 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 12 B) 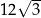 C) 6 D)
C) 6 D) 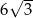
Pole równoległoboku o bokach długości 6 cm i 10 cm i kącie rozwartym o mierze 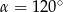 jest równe
jest równe
A) 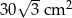 B)
B) 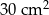 C)
C) 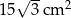 D)
D) 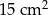
Pole równoległoboku o bokach długości 4 i 7 oraz kącie rozwartym 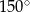 jest równe
jest równe
A) 14 B) 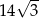 C)
C) 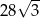 D) 28
D) 28
Boki równoległoboku mają długości 6 i 10, a kąt rozwarty między tymi bokami ma miarę 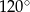 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 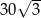 B) 30 C)
B) 30 C) 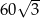 D) 60
D) 60
Różnica miar dwóch kątów rozwartych trapezu jest równa 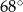 . Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
. Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
A) 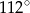 B)
B) 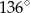 C)
C) 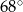 D)
D) 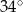
Pole trójkąta równobocznego wpisanego w koło o polu 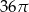 jest równe
jest równe
A) 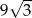 B) 81 C)
B) 81 C) 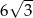 D)
D)