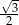Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 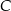 . Środkowa
. Środkowa 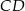 tworzy z przyprostokątną
tworzy z przyprostokątną 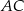 kąt
kąt 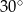 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 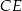 trójkąta ma miarę
trójkąta ma miarę
A) 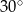 B)
B) 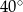 C)
C) 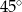 D)
D) 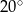
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Prostokątny/Kąty, funkcje trygonometryczne
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 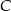 . Środkowa
. Środkowa 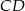 tworzy z przyprostokątną
tworzy z przyprostokątną 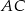 kąt
kąt 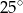 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 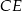 trójkąta ma miarę
trójkąta ma miarę
A) 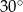 B)
B) 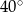 C)
C) 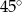 D)
D) 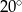
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 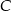 . Środkowa
. Środkowa 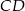 tworzy z przyprostokątną
tworzy z przyprostokątną 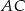 kąt
kąt 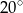 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 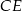 trójkąta ma miarę
trójkąta ma miarę
A) 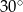 B)
B) 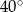 C)
C) 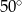 D)
D) 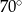
Przyprostokątna 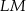 trójkąta prostokątnego
trójkąta prostokątnego 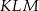 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 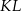 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
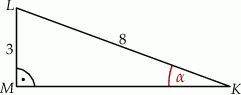
Wtedy miara  kąta ostrego
kąta ostrego 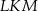 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 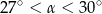 B)
B) 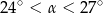 C)
C) 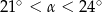 D)
D) 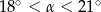
Przyprostokątna 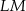 trójkąta prostokątnego
trójkąta prostokątnego 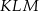 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 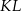 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
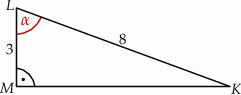
Wtedy miara  kąta ostrego
kąta ostrego 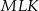 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 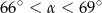 B)
B) 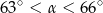 C)
C) 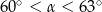 D)
D) 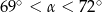
W trójkącie prostokątnym kąty ostre oznaczono  i
i 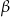 ,
, 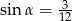 . Jaką miarę ma
. Jaką miarę ma 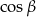 ?
?
A) 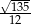 B)
B) 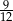 C)
C) 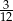 D)
D) 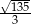
Przyprostokątne trójkąta prostokątnego mają długości 1 i 7. Sinus najmniejszego kąta tego trójkąta jest równy
A) 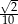 B)
B) 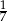 C)
C) 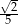 D)
D) 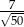
Przyprostokątne trójkąta prostokątnego mają długości 2 i 6. Sinus najmniejszego kąta tego trójkąta jest równy
A) 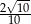 B)
B) 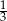 C)
C) 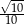 D)
D) 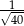
Przyprostokątne trójkąta prostokątnego mają długości 8 i 6. Sinus większego z kątów ostrych tego trójkąta jest równy
A)  B)
B)  C)
C)  D)
D) 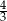
Przyprostokątne trójkąta prostokątnego mają długości 3 i 9. Sinus najmniejszego kąta tego trójkąta jest równy
A) 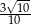 B)
B) 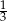 C)
C) 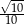 D)
D) 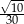
Przyprostokątne w trójkącie prostokątnym mają długości 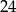 i
i 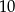 . Sinus najmniejszego kąta jest równy
. Sinus najmniejszego kąta jest równy
A) 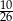 B)
B) 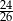 C)
C) 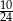 D)
D) 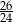
W trójkącie prostokątnym o długościach przyprostokątnych 2 i 5 cosinus większego z kątów ostrych jest równy
A)  B)
B)  C)
C) 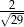 D)
D) 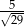
Przyprostokątna 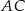 trójkąta prostokątnego
trójkąta prostokątnego 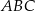 ma długość 6, a przeciwprostokątna
ma długość 6, a przeciwprostokątna 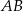 ma długość
ma długość 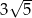 . Wtedy tangens kąta ostrego
. Wtedy tangens kąta ostrego 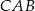 tego trójkąta jest równy
tego trójkąta jest równy
A) 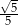 B)
B) 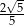 C)
C) 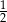 D) 2
D) 2
Kąt  jest kątem ostrym w trójkącie prostokątnym i
jest kątem ostrym w trójkącie prostokątnym i 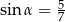 . Wówczas
. Wówczas
A) 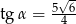 B)
B) 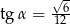 C)
C) 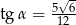 D)
D) 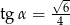
W trójkącie prostokątnym 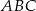 , w którym
, w którym 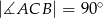 , na boku
, na boku 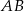 wybrano punkt
wybrano punkt 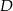 taki, że
taki, że 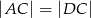 (zobacz rysunek).
(zobacz rysunek).
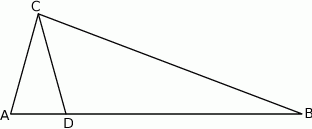
Wynika stąd, że różnica miar kątów 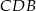 i
i 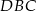 jest równa
jest równa
A) 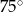 B)
B) 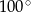 C)
C) 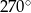 D)
D) 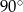
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 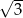 . Zatem
. Zatem
A) 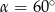 B)
B) 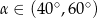 C)
C) 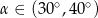 D)
D) 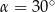
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 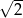 . Zatem
. Zatem
A) 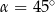 B)
B) 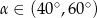 C)
C) 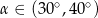 D)
D) 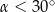
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
A) 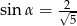 B)
B) 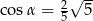 C)
C) 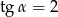 D)
D) 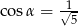
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Natomiast przeciwprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Natomiast przeciwprostokątna ma długość 6 cm. Zatem
A) 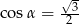 B)
B) 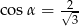 C)
C) 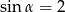 D)
D) 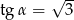
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
A) 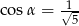 B)
B) 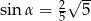 C)
C) 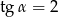 D)
D) 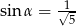
Dany jest trójkąt prostokątny 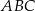 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 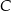 . Jeśli
. Jeśli 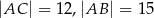 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A)  B)
B)  C)
C)  D)
D) 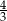
W trójkącie prostokątnym długość przeciwprostokątnej wynosi 8 i jednej z przyprostokątnych 6. Tangens mniejszego kąta ostrego tego trójkąta jest równy
A)  B)
B) 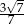 C)
C) 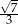 D)
D) 
Dany jest trójkąt prostokątny 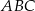 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 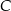 . Jeśli
. Jeśli 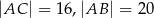 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A)  B)
B)  C)
C) 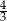 D)
D) 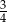
Dany jest trójkąt prostokątny 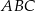 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 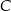 . Jeśli
. Jeśli 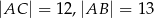 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A) 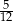 B)
B) 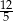 C)
C) 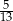 D)
D) 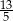
Jedna z przyprostokątnych trójkąta prostokątnego ma długość 15 cm, a przeciwprostokątna 17 cm. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 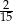 B)
B) 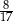 C)
C) 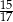 D)
D) 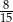
Trójkąt prostokątny ma boki długości 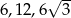 i kąty ostre
i kąty ostre 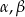 . Kąt
. Kąt 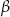 leży naprzeciw boku długości
leży naprzeciw boku długości 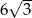 . Zatem
. Zatem
A) 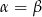 B)
B) 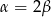 C)
C) 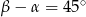 D)
D) 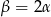
Trójkąt prostokątny ma boki długości 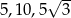 i kąty ostre
i kąty ostre 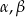 . Kąt
. Kąt 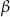 leży naprzeciw boku długości
leży naprzeciw boku długości 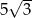 . Zatem
. Zatem
A) 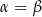 B)
B) 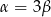 C)
C) 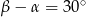 D)
D) 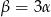
Trójkąt prostokątny ma boki długości 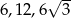 i kąty ostre
i kąty ostre 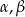 . Kąt
. Kąt 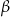 leży naprzeciw boku długości 6. Zatem
leży naprzeciw boku długości 6. Zatem
A) 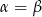 B)
B) 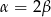 C)
C) 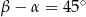 D)
D) 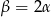
W trójkącie prostokątnym miary kątów ostrych są równe  i
i 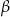 . Wartość wyrażenia
. Wartość wyrażenia 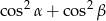 jest równa
jest równa
A) 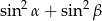 B)
B) 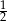 C)
C) 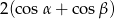 D)
D)