Na rysunkach poniżej znajdują się wykresy dwóch funkcji: 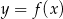 oraz
oraz 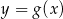 .
.
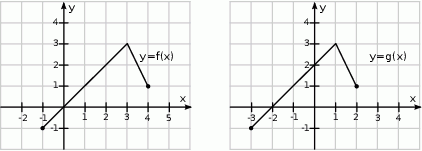
Zatem:
A) 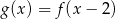 B)
B) 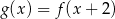
C) 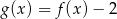 D)
D) 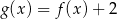
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunkach poniżej znajdują się wykresy dwóch funkcji: 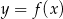 oraz
oraz 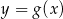 .
.
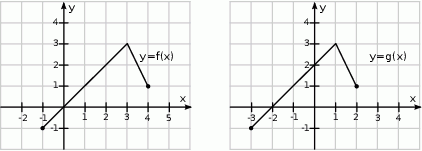
Zatem:
A) 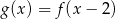 B)
B) 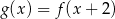
C) 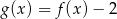 D)
D) 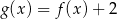
Na rysunku 1 przedstawiony jest wykres funkcji 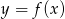 określonej dla
określonej dla 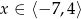 .
.
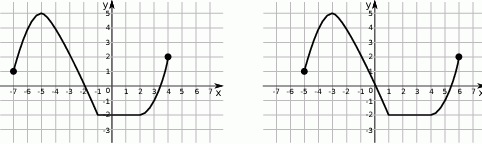
Rysunek 2 przedstawia wykres funkcji
A) 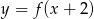 B)
B) 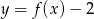 C)
C) 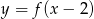 D)
D) 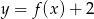
Na rysunku 1 przedstawiony jest wykres funkcji 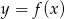 określonej dla
określonej dla 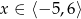 .
.
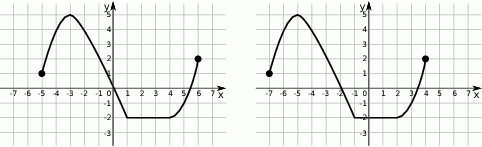
Rysunek 2 przedstawia wykres funkcji
A) 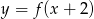 B)
B) 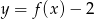 C)
C) 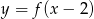 D)
D) 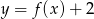
Na rysunku 1. przedstawiono wykres funkcji 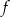 określonej na zbiorze
określonej na zbiorze 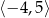 . Funkcję
. Funkcję 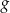 określono za pomocą funkcji
określono za pomocą funkcji 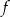 . Wykres funkcji
. Wykres funkcji 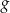 przedstawiono na rysunku 2.
przedstawiono na rysunku 2.
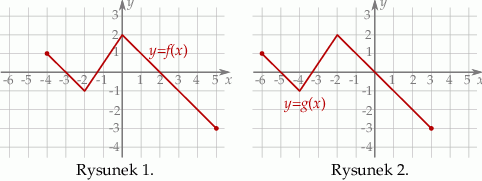
Wynika stąd, że
A) 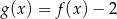 B)
B) 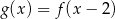
C) 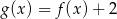 D)
D) 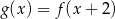
Na rysunku, w układzie współrzędnych 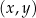 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 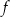 .
.
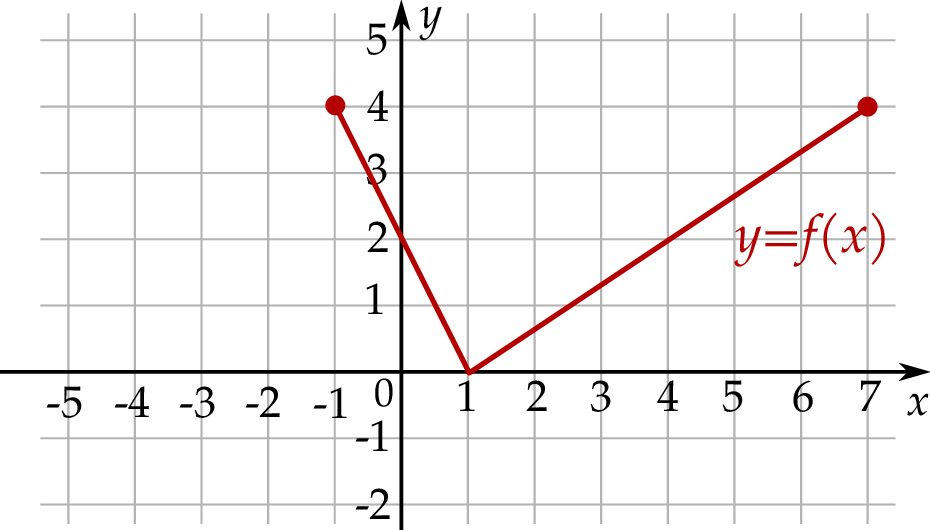
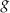 , powstałej w wyniku przesunięcia równoległego wykresu funkcji
, powstałej w wyniku przesunięcia równoległego wykresu funkcji 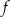 wzdłuż osi
wzdłuż osi 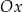 o 4 jednostki w lewo.
o 4 jednostki w lewo. 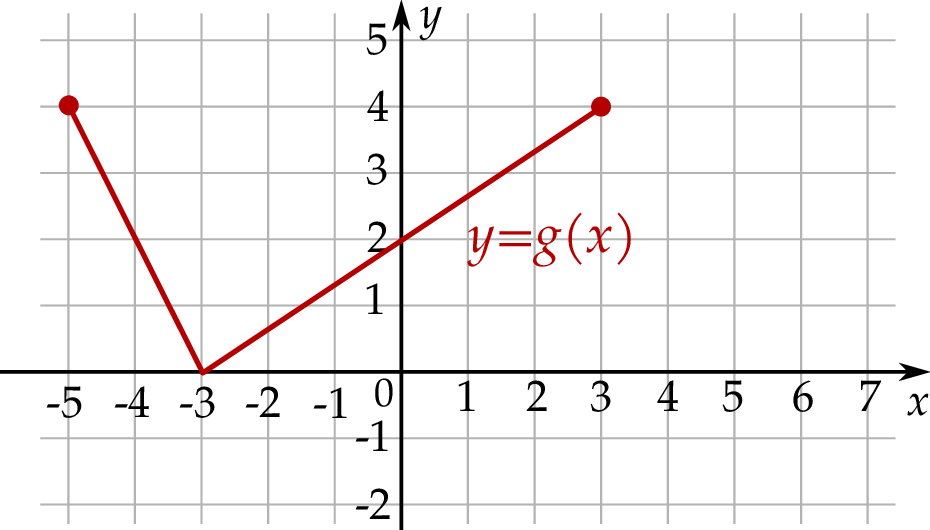
Funkcje 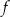 i
i 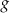 są powiązane zależnością
są powiązane zależnością
A) 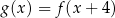 B)
B) 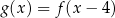
C) 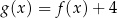 D)
D) 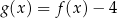
W kartezjańskim układzie współrzędnych 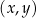 narysowano wykres funkcji
narysowano wykres funkcji 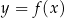 (zobacz rysunek).
(zobacz rysunek).
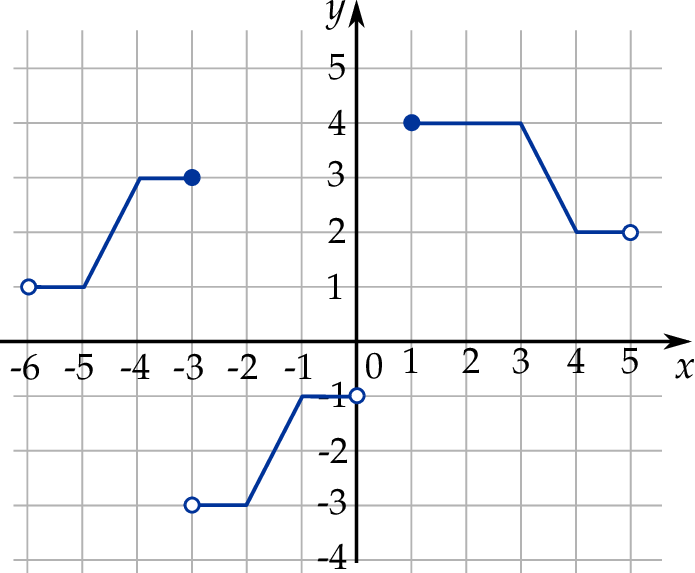
Dziedziną funkcji 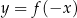 jest zbiór
jest zbiór
A) 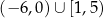 B)
B) 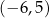 C)
C) ![(− 3,− 1)∪ (1,4]](https://img.zadania.info/zad/4829582/HzadT6x.png)
D) 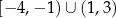 E)
E) ![(− 5,− 1]∪ (0,6)](https://img.zadania.info/zad/4829582/HzadT8x.png) F)
F) 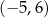
Na poniższym rysunku przedstawiono wykres funkcji 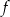 określonej w zbiorze
określonej w zbiorze 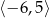 .
.
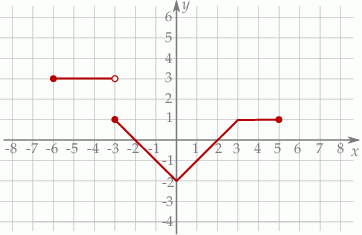
Funkcja 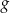 jest określona wzorem
jest określona wzorem 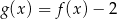 dla
dla 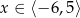 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Liczba 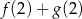 jest równa
jest równa 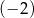 .
.
B) Zbiory wartości funkcji 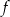 i
i 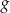 są równe.
są równe.
C) Funkcje 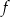 i
i 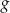 mają te same miejsca zerowe.
mają te same miejsca zerowe.
D) Punkt 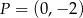 należy do wykresów funkcji
należy do wykresów funkcji 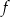 i
i 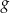 .
.
Na poniższym rysunku przedstawiono wykres funkcji 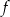 określonej w zbiorze
określonej w zbiorze 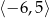 .
.
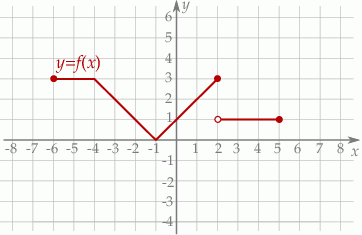
Funkcja 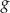 jest określona wzorem
jest określona wzorem 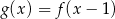 dla
dla 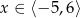 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Liczba 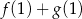 jest równa 2.
jest równa 2.
B) Zbiory wartości funkcji 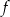 i
i 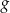 są równe.
są równe.
C) Funkcje 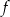 i
i 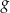 mają takie same miejsca zerowe.
mają takie same miejsca zerowe.
D) Punkt 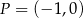 należy do wykresów funkcji
należy do wykresów funkcji 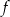 i
i 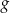 .
.
Na rysunku przedstawiony jest wykres funkcji 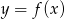 .
.
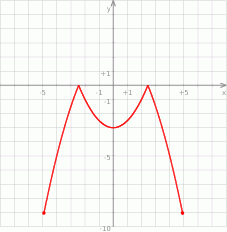
Które z równań ma dokładnie trzy rozwiązania?
A) 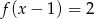 B)
B) 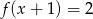 C)
C) 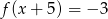 D)
D) 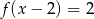
Na rysunku przedstawiony jest wykres funkcji 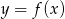 .
.
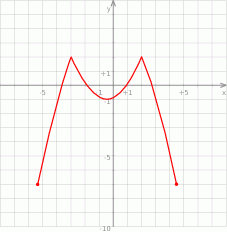
Które z równań ma dokładnie trzy rozwiązania?
A) 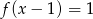 B)
B) 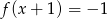 C)
C) 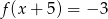 D)
D) 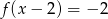
Na rysunku 1 jest przedstawiony wykres funkcji 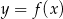 .
.
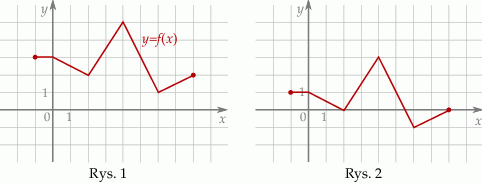
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 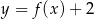 B)
B) 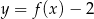 C)
C) 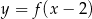 D)
D) 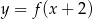
Na rysunku 1 jest przedstawiony wykres funkcji 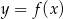 .
.
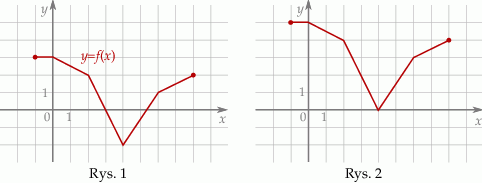
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 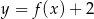 B)
B) 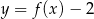 C)
C) 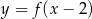 D)
D) 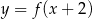
Na poniższych rysunkach przedstawiono wykresy funkcji 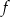 i
i 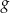 .
.
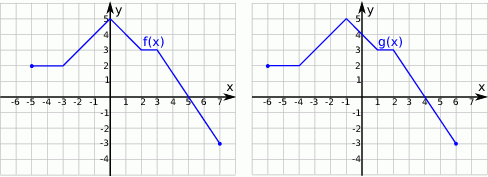
Funkcja 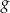 jest określona wzorem
jest określona wzorem
A) 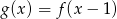 B)
B) 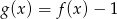 C)
C) 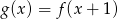 D)
D) 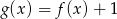
Na poniższych rysunkach przedstawiono wykresy funkcji 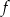 i
i 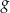 .
.
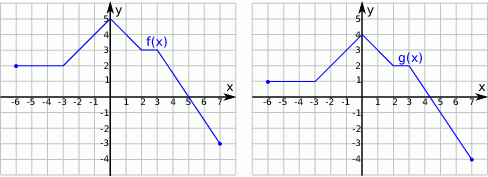
Funkcja 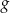 jest określona wzorem
jest określona wzorem
A) 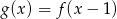 B)
B) 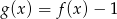 C)
C) 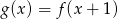 D)
D) 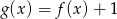
W kartezjańskim układzie współrzędnych 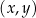 narysowano wykres funkcji
narysowano wykres funkcji 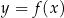 (zobacz rysunek).
(zobacz rysunek).
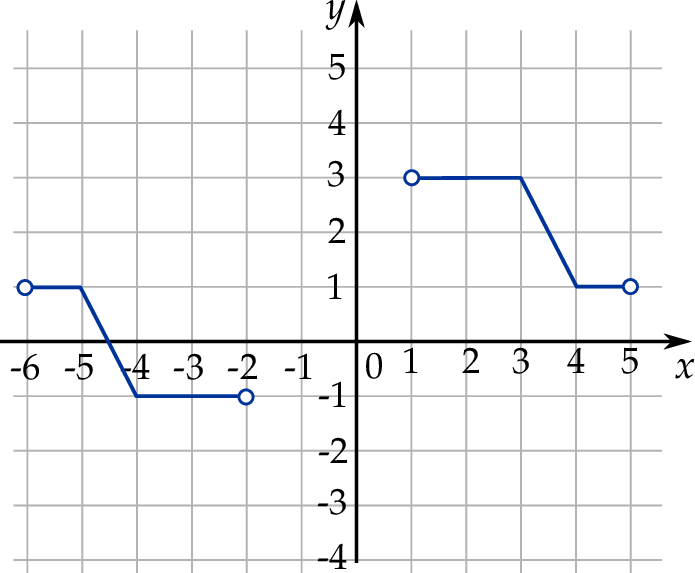
Zbiorem wartości funkcji 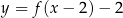 jest zbiór
jest zbiór
A) ![[− 3,1]](https://img.zadania.info/zad/6094235/HzadT4x.png) B)
B) ![[− 1 ,3 ]](https://img.zadania.info/zad/6094235/HzadT5x.png) C)
C) 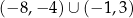
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zad/6094235/HzadT7x.png) E)
E) ![[1,5]](https://img.zadania.info/zad/6094235/HzadT8x.png) F)
F) ![[− 5,− 3]](https://img.zadania.info/zad/6094235/HzadT9x.png)
Funkcja 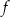 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  . Fragment wykresu funkcji
. Fragment wykresu funkcji 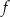 przedstawiono na poniższym rysunku.
przedstawiono na poniższym rysunku.
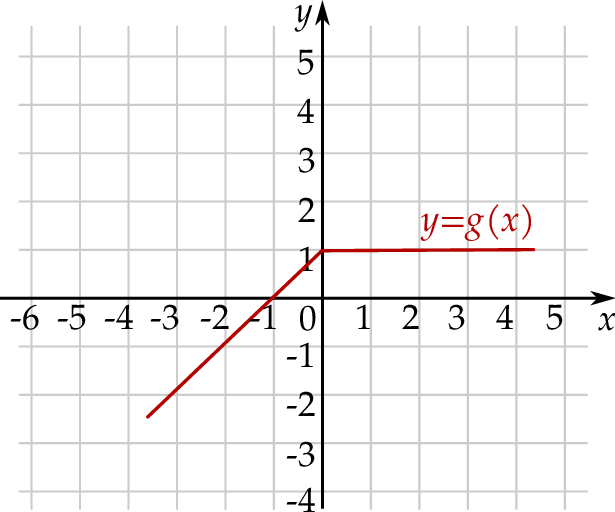
Funkcja 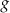 jest określona wzorem
jest określona wzorem 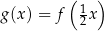 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wskaż rysunek, na którym przedstawiony jest wykres funkcji
. Wskaż rysunek, na którym przedstawiony jest wykres funkcji 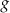 .
.
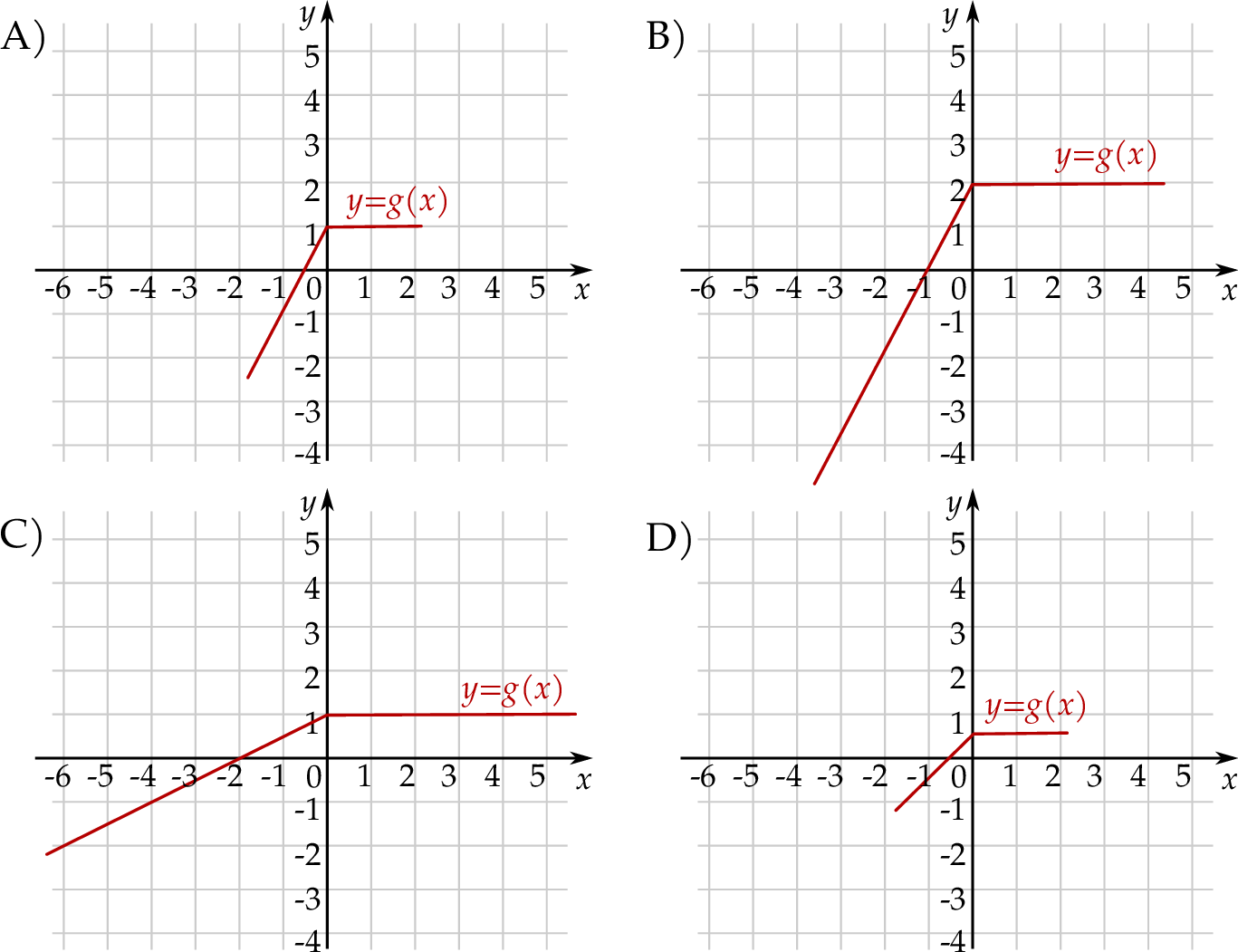
Na rysunku przedstawiono fragment wykresu pewnej funkcji 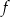 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  . Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji
. Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 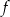 .
.
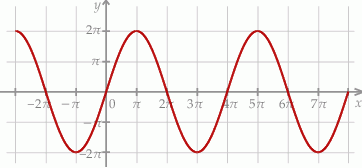
A) 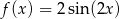 B)
B) 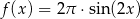
C) 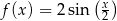 D)
D) 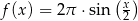
Na rysunku przedstawiono fragment wykresu pewnej funkcji 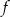 . Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji
. Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 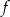 .
.
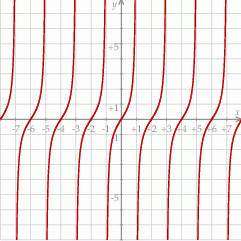
A) 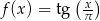 B)
B) 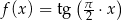
C) 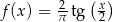 D)
D) 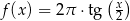
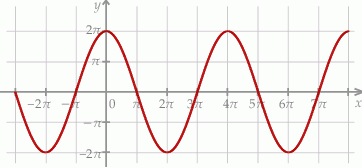
Na rysunku przedstawiono fragment wykresu pewnej funkcji 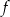 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  . Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji
. Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 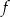 .
.
A) 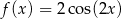 B)
B) 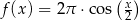
C) 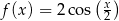 D)
D) 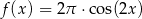
Na rysunku przedstawiony jest wykres funkcji 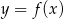 . Dziedziną funkcji
. Dziedziną funkcji 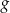 , gdzie
, gdzie 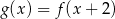 jest zbiór
jest zbiór
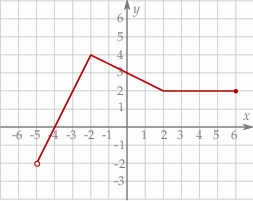
A) 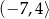 B)
B) 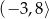 C)
C) 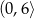 D)
D) 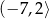
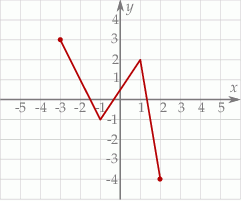
Jeśli na rysunku przedstawiony jest wykres funkcji 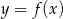 , to dziedziną funkcji
, to dziedziną funkcji 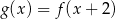 jest zbiór
jest zbiór
A) 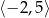 B)
B) 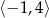 C)
C) 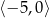 D)
D) 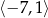
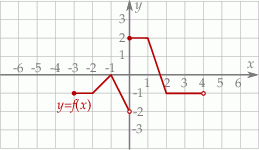
Jeśli na rysunku przedstawiony jest wykres funkcji 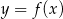 , to dziedziną funkcji
, to dziedziną funkcji 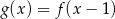 jest zbiór
jest zbiór
A) 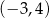 B)
B) 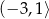 C)
C) 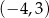 D)
D) 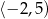
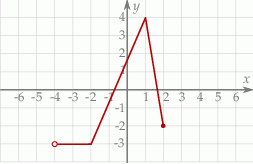
Na rysunku przedstawiony jest wykres funkcji 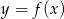 . Dziedziną funkcji
. Dziedziną funkcji 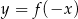 jest
jest
A) 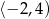 B)
B) 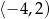 C)
C) 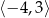 D)
D) 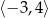
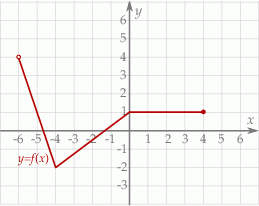
Na rysunku przedstawiony jest wykres funkcji 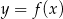 . Dziedziną funkcji
. Dziedziną funkcji 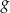 , gdzie
, gdzie 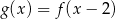 jest zbiór
jest zbiór
A) 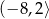 B)
B) 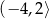 C)
C) 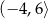 D)
D) 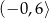
Dana jest funkcja 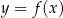 określona dla
określona dla 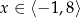 , której wykres jest przedstawiony na rysunku.
, której wykres jest przedstawiony na rysunku.
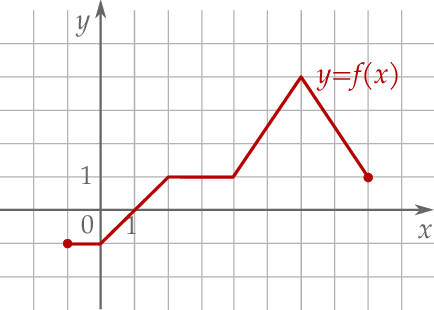
Wskaż zbiór wartości tej funkcji.
A) 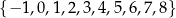 B)
B) 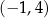 C)
C) 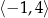 D)
D) 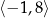
Zbiorem wartości funkcji 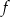 , której wykres przedstawiono na wykresie poniżej jest przedział
, której wykres przedstawiono na wykresie poniżej jest przedział
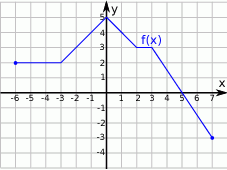
A) 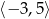 B)
B) 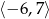 C)
C) 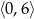 D)
D) 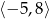
Na rysunku przedstawiono wykres funkcji 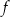 .
.
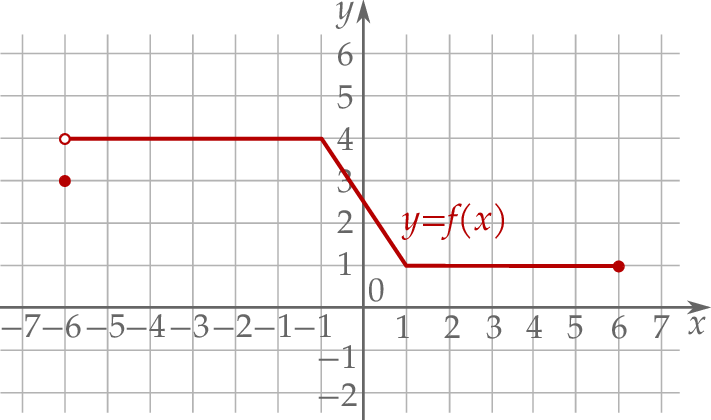
Zbiorem wartości tej funkcji jest
A) ![(− 6,6]](https://img.zadania.info/zad/5671019/HzadT2x.png) B)
B) 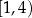 C)
C) ![[1,4]](https://img.zadania.info/zad/5671019/HzadT4x.png) D)
D) ![[− 6,6]](https://img.zadania.info/zad/5671019/HzadT5x.png)
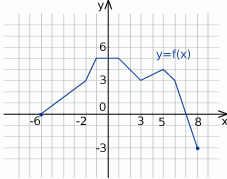
Zbiorem wartości funkcji 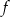 , której wykres przedstawiono poniżej jest
, której wykres przedstawiono poniżej jest
A) 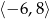 B)
B) 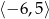 C)
C) 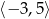 D)
D) 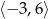
Dana jest funkcja 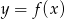 , której wykres jest przedstawiony na rysunku.
, której wykres jest przedstawiony na rysunku.
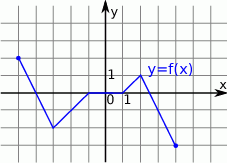
Wskaż zbiór wartości tej funkcji.
A) 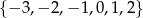 B)
B) 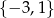 C)
C) 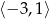 D)
D) 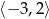
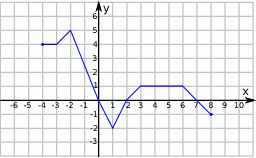
Zbiorem wartości funkcji 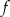 , której wykres przedstawiono poniżej jest
, której wykres przedstawiono poniżej jest
A) 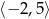 B)
B) 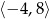 C)
C) 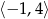 D)
D) 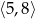
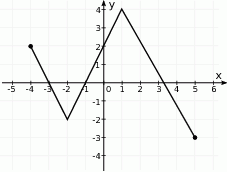
Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest przedział:
A) 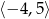 B)
B) 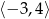 C)
C) 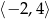 D)
D) 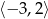
Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest przedział:
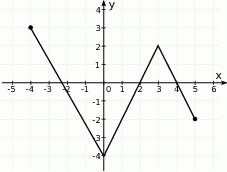
A) 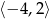 B)
B) 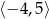 C)
C) 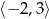 D)
D) 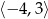
Na rysunku, w kartezjańskim układzie współrzędnych 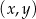 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 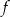 określonej dla każdego
określonej dla każdego 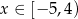 . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
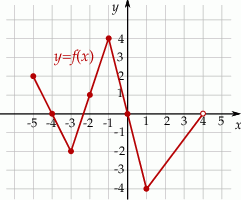
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dla każdego argumentu z przedziału 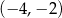 funkcja funkcja 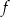 przyjmuje wartości ujemne. przyjmuje wartości ujemne. | P | F |
Funkcja 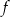 ma trzy miejsca zerowe. ma trzy miejsca zerowe. | P | F |
Na rysunku, w kartezjańskim układzie współrzędnych 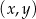 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 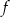 określonej dla każdego
określonej dla każdego ![x ∈ (− 4,5]](https://img.zadania.info/zad/8434319/HzadT2x.gif) . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
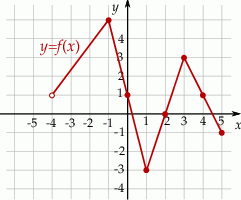
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dla każdego argumentu z przedziału 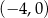 funkcja funkcja 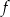 przyjmuje wartości dodatnie. przyjmuje wartości dodatnie. | P | F |
Funkcja 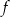 ma cztery miejsca zerowe. ma cztery miejsca zerowe. | P | F |
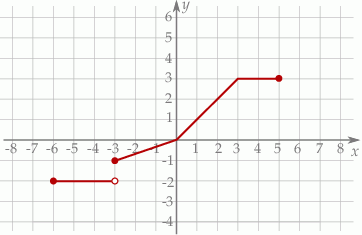
Na poniższym rysunku przedstawiono wykres funkcji 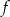 określonej w zbiorze
określonej w zbiorze 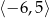 .
.
Funkcja 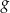 jest określona wzorem
jest określona wzorem 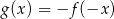 dla
dla 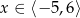 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Zbiór wartości funkcji 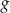 nie zawiera liczb dodatnich.
nie zawiera liczb dodatnich.
B) Punkt 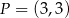 należy do wykresów funkcji
należy do wykresów funkcji 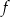 i
i 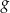 .
.
C) Równanie 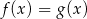 ma nieskończenie wiele rozwiązań.
ma nieskończenie wiele rozwiązań.
D) Jest tylko jedna liczba  spełniająca nierówność
spełniająca nierówność 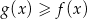 .
.
Na rysunku przedstawione są wykresy funkcji 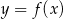 oraz
oraz 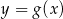 .
.
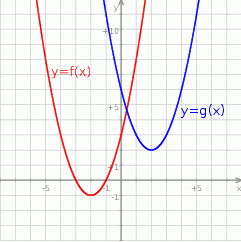
Wówczas :
A) 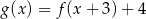 B)
B) 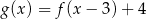
C) 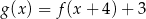 D)
D) 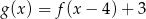
Na rysunku przedstawione są wykresy funkcji 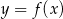 oraz
oraz 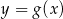 .
.
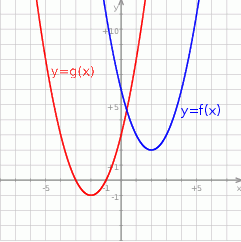
Wówczas :
A) 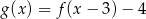 B)
B) 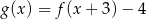
C) 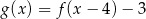 D)
D) 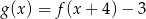
Na rysunkach przedstawione są wykresy funkcji 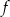 i
i 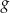 .
.
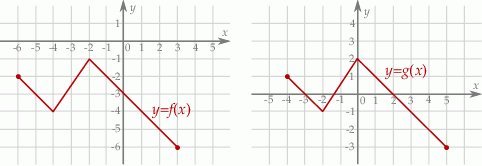
Wykres funkcji 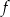 przekształcono i otrzymano wykres funkcji
przekształcono i otrzymano wykres funkcji 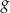 , zatem
, zatem
A) 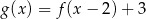 B)
B) 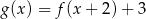
C) 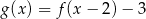 D)
D) 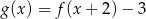
Na rysunkach przedstawione są wykresy funkcji 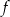 i
i 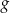 .
.
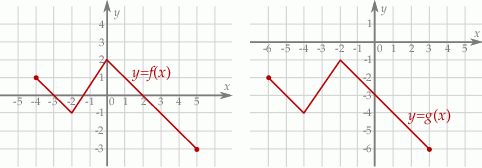
Wykres funkcji 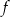 przekształcono i otrzymano wykres funkcji
przekształcono i otrzymano wykres funkcji 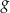 , zatem
, zatem
A) 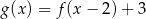 B)
B) 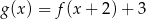
C) 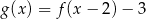 D)
D) 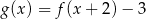
Na rysunku, w kartezjańskim układzie współrzędnych 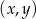 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 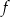 określonej dla każdego
określonej dla każdego ![x ∈ (− 6,5]](https://img.zadania.info/zad/7384757/HzadT2x.gif) . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
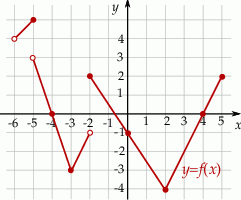
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 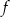 jest malejąca na przedziale jest malejąca na przedziale ![[− 2,2]](https://img.zadania.info/zad/7384757/HzadT5x.gif) . . | P | F |
Dla każdego argumentu z przedziału ![[− 4,− 2]](https://img.zadania.info/zad/7384757/HzadT6x.gif) funkcja funkcja 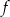 przyjmuje wartości niedodatnie. przyjmuje wartości niedodatnie. | P | F |
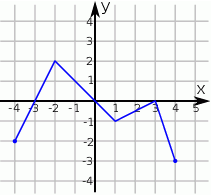
Rysunek przedstawia wykres pewnej funkcji 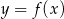 , określonej dla
, określonej dla 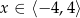 . Zbiór wszystkich argumentów, dla których funkcja
. Zbiór wszystkich argumentów, dla których funkcja 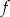 przyjmuje wartości niedodatnie, to zbiór:
przyjmuje wartości niedodatnie, to zbiór:
A) 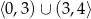 B)
B) 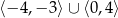
C) 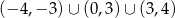 D)
D) 
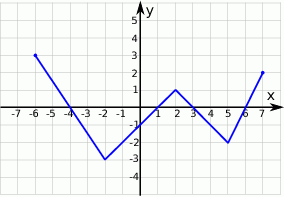
Na rysunku przedstawiony jest wykres pewnej funkcji 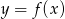 . Przyjmuje ona wartości niedodatnie dla argumentów:
. Przyjmuje ona wartości niedodatnie dla argumentów:
A) 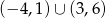 B)
B) 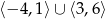 C)
C) 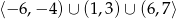 D)
D) 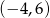
Na rysunku przedstawiono wykres funkcji 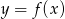 .
.
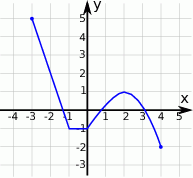
W którym z przedziałów, funkcja przyjmuje wartość 1?
A) 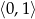 B)
B) 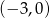 C)
C) 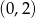 D)
D) 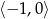
W kartezjańskim układzie współrzędnych 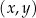 narysowano wykres funkcji
narysowano wykres funkcji 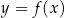 (zobacz rysunek).
(zobacz rysunek).
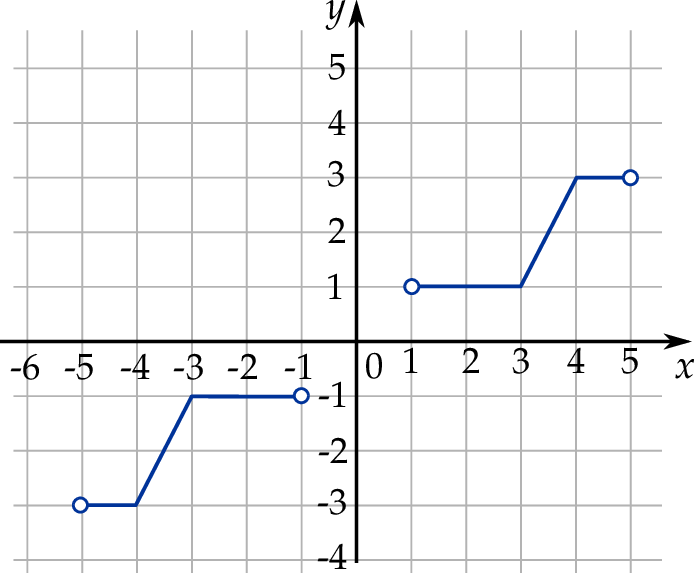
Zbiorem wartości funkcji 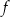 jest zbiór
jest zbiór
A) ![[− 3,− 1]∪ [1,3]](https://img.zadania.info/zad/7474248/HzadT4x.png) B)
B) 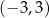 C)
C) 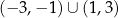
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zad/7474248/HzadT7x.png) E)
E) 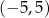 F)
F) 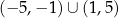
W kartezjańskim układzie współrzędnych 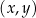 narysowano wykres funkcji
narysowano wykres funkcji 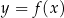 (zobacz rysunek).
(zobacz rysunek).
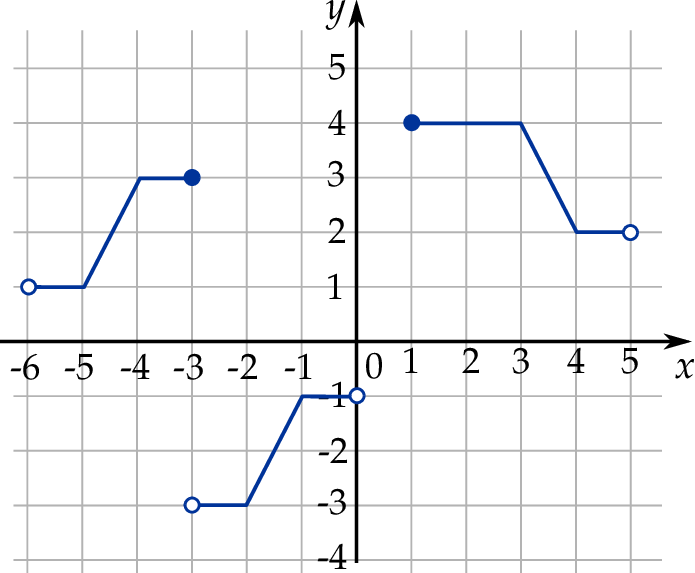
Zbiorem wartości funkcji 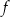 jest zbiór
jest zbiór
A) 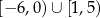 B)
B) ![[− 3,4]](https://img.zadania.info/zad/5016823/HzadT5x.png) C)
C) 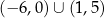
D) ![[− 3,− 1)∪ (1 ,4 ]](https://img.zadania.info/zad/5016823/HzadT7x.png) E)
E) ![(− 3,4 ]](https://img.zadania.info/zad/5016823/HzadT8x.png) F)
F) ![[− 3,− 1] ∪ [1 ,4 ]](https://img.zadania.info/zad/5016823/HzadT9x.png)
Na rysunku 1 jest przedstawiony wykres funkcji 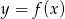 .
.
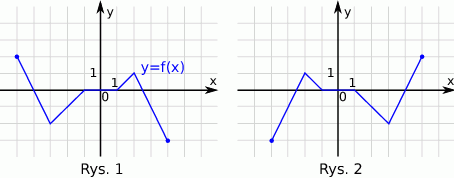
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 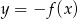 B)
B) 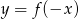 C)
C) 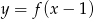 D)
D) 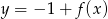
Na rysunku 1. jest przedstawiony wykres funkcji 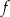 , a na rysunku 2. – wykres funkcji
, a na rysunku 2. – wykres funkcji 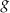 .
.
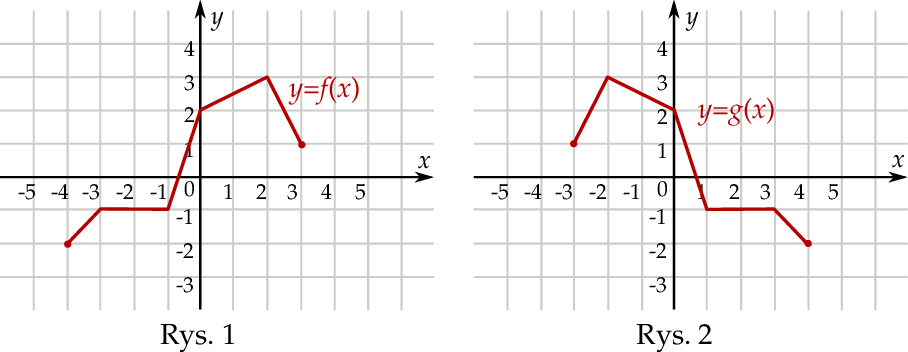
Funkcja 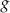 jest określona wzorem
jest określona wzorem
A) 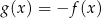 B)
B) 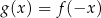 C)
C) 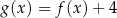 D)
D) 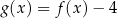
Na rysunku 1 jest przedstawiony wykres funkcji 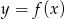 .
.
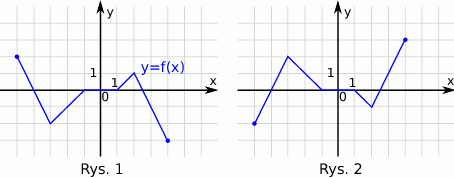
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 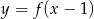 B)
B) 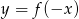 C)
C) 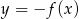 D)
D) 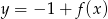
Na rysunku 1. jest przedstawiony wykres funkcji 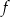 , a na rysunku 2. – wykres funkcji
, a na rysunku 2. – wykres funkcji 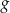 .
.
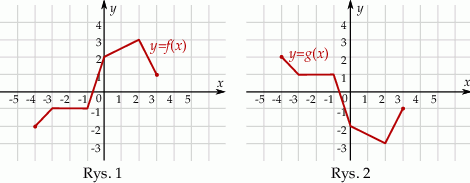
Funkcja 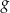 jest określona wzorem
jest określona wzorem
A) 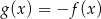 B)
B) 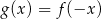 C)
C) 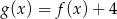 D)
D) 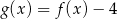
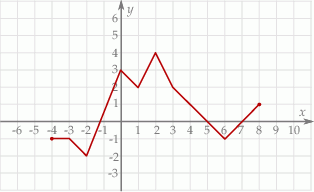
Korzystając z danego wykresu funkcji 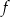 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą
A) 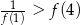 B)
B) ![[f (−3 )]2 < f (4)](https://img.zadania.info/zad/7980393/HzadT3x.gif) C)
C) 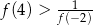 D)
D) ![2 f(3) > [f (3)]](https://img.zadania.info/zad/7980393/HzadT5x.gif)
Rysunek przedstawia wykres funkcji 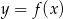 .
.
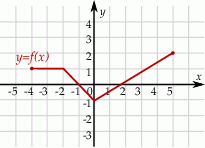
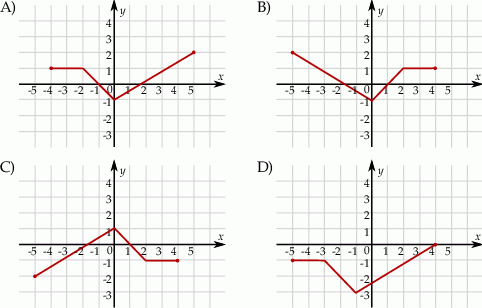
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 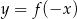 .
.
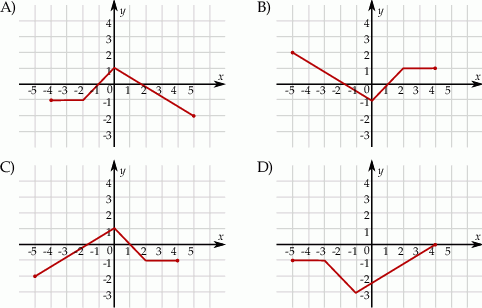
Rysunek przedstawia wykres funkcji 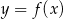 .
.
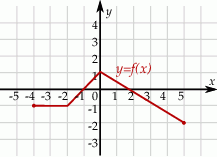
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 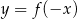 .
.
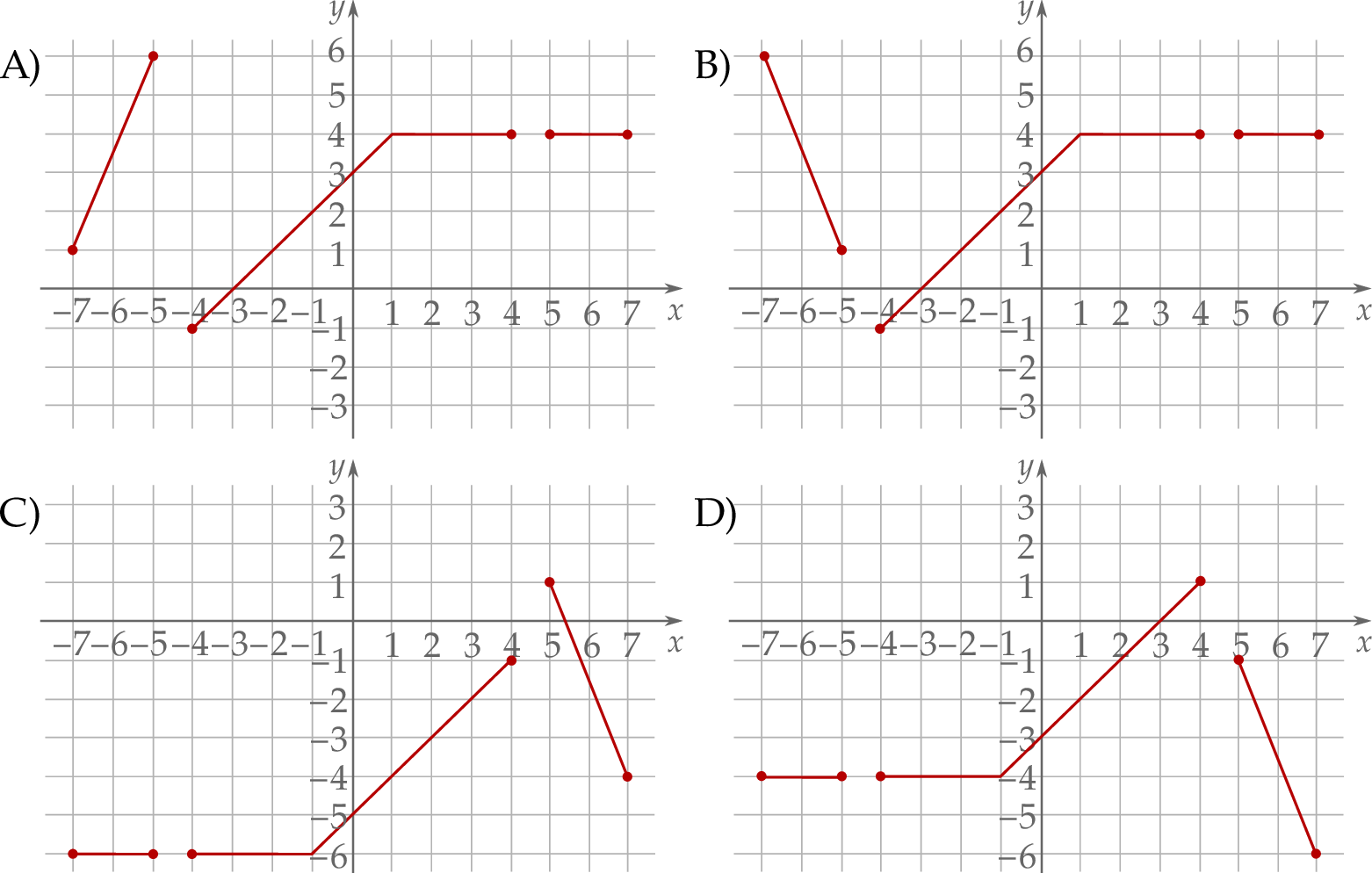
W kartezjańskim układzie współrzędnych 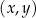 narysowano wykres funkcji
narysowano wykres funkcji 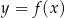 (zobacz rysunek).
(zobacz rysunek).
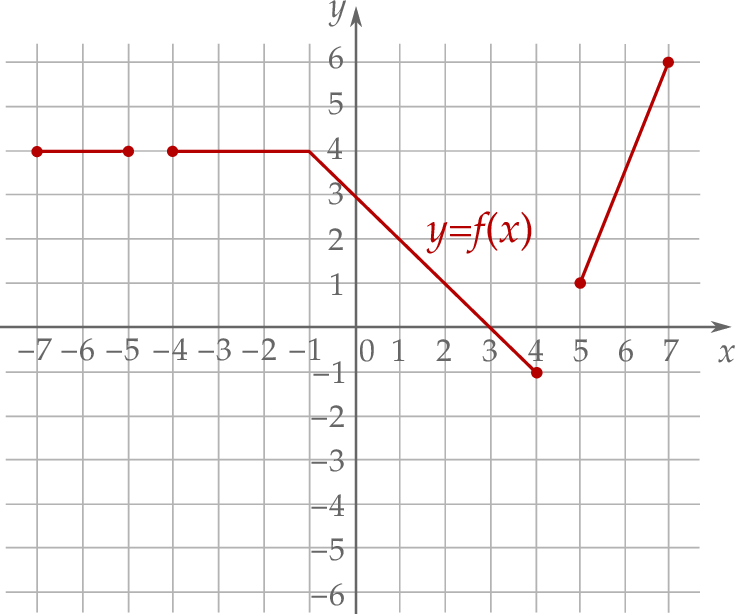
Funkcja 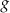 jest określona za pomocą funkcji
jest określona za pomocą funkcji 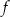 następująco:
następująco: 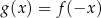 dla każdego
dla każdego ![x ∈ [− 7,− 5] ∪ [− 4,4 ]∪ [5 ,7]](https://img.zadania.info/zad/7097707/HzadT6x.png) . Na jednym z rysunków A–D przedstawiono, w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono, w kartezjańskim układzie współrzędnych 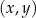 , wykres funkcji
, wykres funkcji 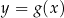 . Wykres funkcji
. Wykres funkcji 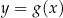 przedstawiono na rysunku
przedstawiono na rysunku