Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 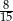 , a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe 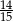 . Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul białych jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul białych jest równe
A) 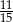 B)
B) 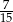 C)
C) 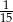 D)
D) 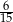
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo
Z pudełka zwierającego losy wygrywające i przegrywające wybieramy dwa losy. Prawdopodobieństwo wylosowania co najmniej jednego losu wygrywającego jest równe 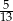 , a prawdopodobieństwo wybrania co najwyżej jednego losu wygrywającego jest równe
, a prawdopodobieństwo wybrania co najwyżej jednego losu wygrywającego jest równe 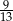 . Wobec tego prawdopodobieństwo wybrania dokładnie dwóch losów wygrywających jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch losów wygrywających jest równe
A) 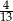 B)
B) 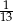 C)
C) 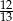 D)
D) 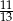
Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli niebieskiej jest równe 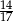 , a prawdopodobieństwo wybrania co najwyżej jednej kuli niebieskiej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli niebieskiej jest równe 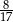 . Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul niebieskich jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul niebieskich jest równe
A) 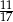 B)
B) 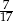 C)
C) 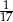 D)
D) 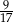
Jeżeli 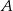 i
i 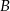 są zdarzeniami losowymi,
są zdarzeniami losowymi, 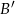 jest zdarzeniem przeciwnym do
jest zdarzeniem przeciwnym do 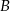 ,
, 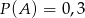 ,
, 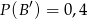 oraz
oraz 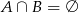 , to
, to 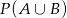 jest równe
jest równe
A) 0,12 B) 0,18 C) 0,6 D) 0,9
Jeżeli 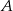 i
i 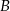 są zdarzeniami losowymi,
są zdarzeniami losowymi, 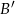 jest zdarzeniem przeciwnym do
jest zdarzeniem przeciwnym do 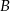 ,
, 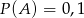 ,
, 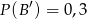 oraz
oraz 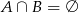 , to
, to 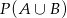 jest równe
jest równe
A) 0,4 B) 0,2 C) 0,8 D) 0,9
Ze zbioru 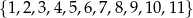 losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę
losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę 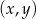 , gdzie
, gdzie  jest pierwszą wylosowaną liczbą,
jest pierwszą wylosowaną liczbą, 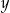 jest drugą wylosowaną liczbą. Wszystkich par
jest drugą wylosowaną liczbą. Wszystkich par 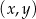 takich, że suma
takich, że suma 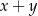 jest liczbą parzystą jest
jest liczbą parzystą jest
A) 20 B) 25 C) 50 D) 61
W pudełku znajdują się dwie kule: niebieska i czerwona. Dziewięciokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie osiem z wylosowanych kul jest tego samego koloru jest równe
A) 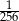 B)
B) 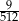 C)
C) 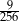 D)
D) 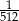
W pudełku znajdują się dwie kule: niebieska i czerwona. Ośmiokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie siedem z wylosowanych kul jest tego samego koloru jest równe
A) 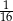 B)
B) 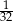 C)
C) 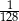 D)
D) 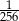
Losujemy jedną liczbę ze zbioru 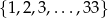 . Niech
. Niech 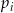 oznacza prawdopodobieństwo otrzymania liczby dającej resztę
oznacza prawdopodobieństwo otrzymania liczby dającej resztę 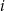 przy dzieleniu przez 10. Wtedy
przy dzieleniu przez 10. Wtedy
A) 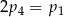 B)
B) 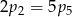 C)
C) 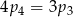 D)
D) 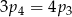
Losujemy jedną liczbę ze zbioru 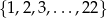 . Niech
. Niech 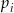 oznacza prawdopodobieństwo otrzymania liczby dającej resztę
oznacza prawdopodobieństwo otrzymania liczby dającej resztę 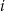 przy dzieleniu przez 4. Wtedy
przy dzieleniu przez 4. Wtedy
A) 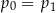 B)
B) 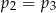 C)
C) 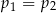 D)
D) 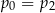
Ze zbioru liczb 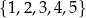 losujemy bez zwracania kolejno dwa razy po jednej liczbie. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
losujemy bez zwracania kolejno dwa razy po jednej liczbie. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania dwóch liczb mniejszych od 4 jest równe prawdopodobieństwu wylosowania dwóch liczb większych od 2. | P | F |
Prawdopodobieństwo tego, że pierwsza liczba jest większa od drugiej jest równe 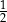 . . | P | F |
W pewnej grupie przyjaciół co czwarta osoba ma na imię Kuba. Losujemy jedną osobę z tej grupy. Prawdopodobieństwo tego, że wylosowana osoba nie ma na imię Kuba, jest równe
A) 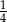 B)
B) 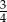 C)
C) 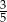 D)
D) 
Ze zbioru liczb naturalnych pięciocyfrowych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 5, jest równe
A)  B)
B) 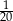 C)
C) 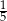 D)
D) 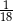
Ze zbioru liczb naturalnych zawartych w przedziale 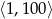 wybieramy losowo jedną. Niech
wybieramy losowo jedną. Niech 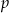 oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 7. Wówczas
oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 7. Wówczas
A) 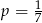 B)
B) 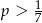 C)
C) 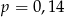 D)
D) 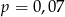
Ze zbioru liczb naturalnych zawartych w przedziale 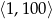 wybieramy losowo jedną. Niech
wybieramy losowo jedną. Niech 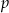 oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 6. Wówczas
oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 6. Wówczas
A) 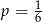 B)
B) 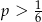 C)
C) 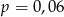 D)
D) 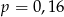
Z talii 52 kart losujemy jedną. Prawdopodobieństwo, że wylosujemy króla lub kiera, jest równe
A) 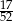 B)
B) 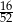 C)
C) 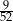 D)
D) 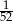
Z talii 24 kart (od dziewiątek) losujemy jedną. Prawdopodobieństwo, że wylosujemy waleta lub trefla, jest równe
A) 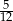 B)
B) 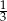 C)
C)  D)
D) 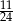
Z talii 52 kart wylosowano jedną kartę. Jakie jest prawdopodobieństwo, że wylosowano kartę pikową lub waleta?
A) 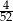 B)
B) 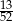 C)
C) 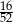 D)
D) 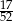
Z talii 52 kart losujemy jedną. Prawdopodobieństwo, że wylosujemy damę lub pika, jest równe
A) 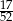 B)
B) 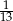 C)
C) 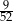 D)
D) 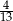
Rzucamy sześć razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sześciu różnych liczb oczek, jest równe
A) 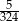 B)
B) 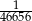 C)
C)  D)
D) 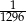
Ze zbioru trzycyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 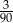 B)
B) 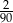 C)
C) 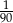 D)
D) 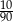
Ze zbioru trzycyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 15 jest równe
A) 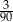 B)
B) 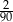 C)
C) 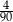 D)
D) 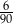
Doświadczenie losowe polega na rzucie trzema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo zdarzenia polegającego na tym, że liczba oczek otrzymanych na kostce jest równa liczbie wylosowanych orłów na monetach jest równe
A) 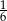 B)
B) 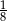 C)
C) 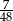 D)
D) 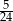
Na loterię przygotowano pulę 100 losów, w tym 4 wygrywające. Po wylosowaniu pewnej liczby losów, wśród których był dokładnie jeden wygrywający, szansa na wygraną była taka sama jak przed rozpoczęciem loterii. Stąd wynika, że wylosowano
A) 4 losy. B) 20 losów. C) 50 losów. D) 25 losów.
Na loterię przygotowano pulę 200 losów, w tym 4 wygrywające. Po wylosowaniu pewnej liczby losów, wśród których były dokładnie dwa wygrywające, szansa na wygraną była taka sama jak przed rozpoczęciem loterii. Stąd wynika, że wylosowano
A) 8 losów. B) 40 losów. C) 100 losów. D) 50 losów.
W pudełku znajdują się wyłącznie kule białe i czarne. Kul czarnych jest 18. Z tego pudełka w sposób losowy wyciągamy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kulę czarną, jest równe  . Liczba kul białych w pudełku, przed wyciągnięciem jednej kuli, była równa
. Liczba kul białych w pudełku, przed wyciągnięciem jednej kuli, była równa
A) 9 B) 12 C) 15 D) 30
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 25% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,75 B) 0,25 C) 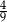 D)
D) 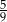
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 40% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,6 B) 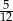 C)
C) 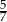 D) 0,4
D) 0,4
Na loterii stosunek liczby losów wygrywających do liczby losów przegrywających jest równy 2 : 7. Zakupiono jeden los z tej loterii. Prawdopodobieństwo zdarzenia polegającego na tym, że zakupiony los jest wygrywający, jest równe
A) 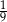 B)
B) 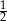 C)
C) 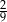 D)
D) 
Na loterii stosunek liczby losów wygrywających do liczby losów przegrywających jest równy 2 : 7. Zakupiono jeden los z tej loterii. Prawdopodobieństwo zdarzenia polegającego na tym, że zakupiony los jest przegrywający, jest równe
A) 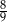 B)
B) 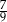 C)
C) 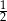 D)
D) 
Kod, który zapisany jest na karcie dostępu, składa się z czterech cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu zmniejszyło się stukrotnie. Ile jeszcze cyfr należy dopisać do kodu?
A) 1 B) 2 C) 100 D) 6
Kod, który zapisany jest na karcie dostępu, składa się z czterech cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu zmniejszyło się tysiąckrotnie. Ile jeszcze cyfr należy dopisać do kodu?
A) 3 B) 2 C) 1000 D) 7
Kod dostępu do sejfu składa się z pięciu cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu zmniejszyło się stukrotnie. Ile cyfr powinien mieć nowy kod?
A) 7 B) 2 C) 100 D) 6
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sumy oczek równej trzy wynosi
A)  B)
B) 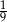 C)
C) 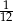 D)
D) 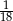
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia w obu rzutach liczby oczek podzielnej przez 3 jest równe
A) 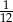 B)
B) 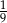 C)
C) 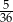 D)
D) 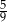
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania pary liczb, których iloczyn jest większy od 20, jest równe
A) 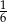 B)
B) 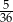 C)
C) 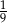 D)
D) 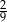
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb wyrzuconych oczek jest liczbą nieparzystą, jest równe
A) 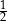 B)
B) 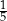 C)
C)  D)
D) 
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania pary liczb, których iloczyn jest większy od 18, jest równe
A) 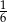 B)
B) 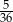 C)
C) 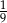 D)
D) 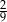
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania parzystej sumy oczek jest równe
A)  B)
B) 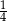 C)
C) 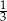 D)
D) 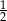
Prawdopodobieństwo zdarzenia, że w rzucie dwiema symetrycznymi kostkami do gry otrzymamy iloczyn oczek równy 6, wynosi
A) 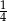 B)
B) 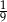 C)
C) 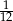 D)
D) 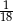
Losujemy rzucając dwukrotnie symetryczną kostką sześcienną. Jakie jest prawdopodobieństwo, że w drugim rzucie wylosujemy o trzy oczka więcej niż w pierwszym?
A) 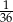 B)
B) 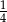 C)
C) 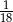 D)
D) 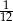
Prawdopodobieństwo zdarzenia, że w rzucie dwiema symetrycznymi kostkami do gry otrzymamy sumę oczek równą 7, wynosi
A)  B)
B) 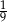 C)
C) 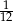 D)
D) 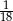
Prawdopodobieństwo zdarzenia, że w rzucie dwiema symetrycznymi kostkami do gry otrzymamy iloczyn oczek równy 4, wynosi
A) 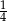 B)
B) 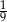 C)
C) 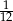 D)
D) 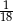
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Niech 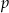 oznacza prawdopodobieństwo zdarzenia, że iloczyn liczb wyrzuconych oczek jest równy 5. Wtedy
oznacza prawdopodobieństwo zdarzenia, że iloczyn liczb wyrzuconych oczek jest równy 5. Wtedy
A) 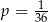 B)
B) 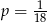 C)
C) 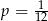 D)
D) 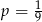
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego do sześciu. Niech 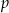 oznacza prawdopodobieństwo otrzymania w drugim rzucie liczby oczek podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania w drugim rzucie liczby oczek podzielnej przez 3. Wtedy
A) 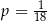 B)
B) 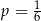 C)
C) 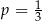 D)
D) 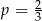
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania iloczynu oczek równego cztery jest równe
A) 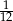 B)
B) 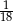 C)
C) 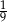 D)
D) 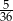
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sumy oczek równej cztery wynosi
A)  B)
B) 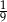 C)
C) 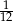 D)
D) 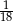
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo dwukrotnego otrzymania pięciu oczek jest równe
A)  B)
B) 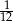 C)
C) 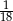 D)
D) 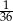
Prawdopodobieństwo zdarzenia, że w rzucie dwiema symetrycznymi kostkami do gry otrzymamy sumę oczek równą 6, wynosi
A) 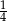 B)
B) 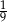 C)
C) 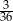 D)
D) 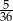
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [19 dag, 21 dag]. Pobrano próbę kontrolną liczącą 50 jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie.
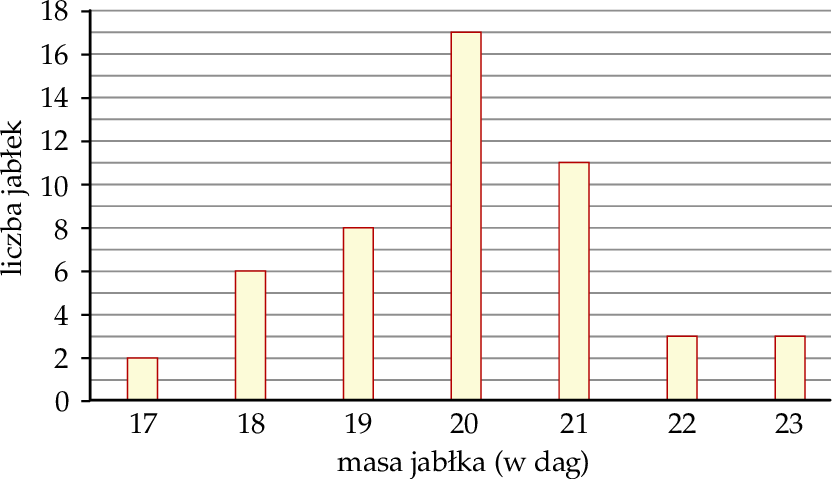
Spośród 50 zważonych jabłek z pobranej próby kontrolnej losujemy jedno jabłko. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowane jabłko spełnia normę jakości, jest równe
A)  B)
B)  C)
C) 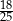 D)
D) 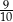
W hurtowni owoców wyselekcjonowana gruszka spełnia normę jakości, gdy jej masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [16 dag, 18 dag]. Pobrano próbę kontrolną liczącą 50 gruszek i następnie zważono każdą z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy gruszek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę gruszki (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę gruszek o określonej masie.
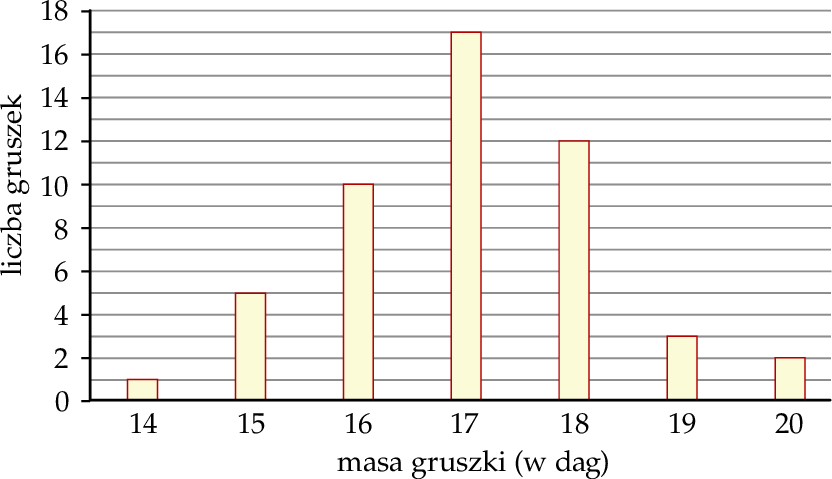
Spośród 50 zważonych gruszek z pobranej próby kontrolnej losujemy jedną gruszkę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana gruszka spełnia normę jakości, jest równe
A) 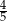 B)
B) 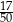 C)
C) 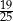 D)
D)