Prawdopodobieństwo zdarzenia 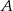 jest równe
jest równe 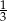 , a prawdopodobieństwo sumy zdarzeń
, a prawdopodobieństwo sumy zdarzeń 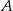 i
i 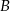 jest równe
jest równe 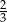 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 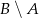 jest równe
jest równe
A) 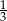 B)
B)  C)
C) 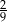 D)
D) 
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo/Bez treści
Prawdopodobieństwo zdarzenia 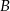 jest równe
jest równe 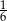 , a prawdopodobieństwo sumy zdarzeń
, a prawdopodobieństwo sumy zdarzeń 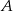 i
i 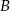 jest równe
jest równe 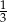 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 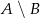 jest równe
jest równe
A) 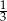 B)
B)  C)
C)  D)
D) 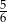
Jeżeli 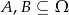 oraz
oraz 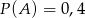 i
i 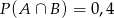 to prawdopodobieństwo
to prawdopodobieństwo 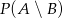 jest równe
jest równe
A) 0,6 B) 0,4 C) 1 D) 0
Niepuste zdarzenia losowe 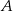 i
i 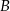 zawarte w
zawarte w 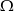 są takie, że
są takie, że 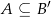 , gdzie
, gdzie 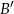 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 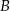 . Wynika stąd, że
. Wynika stąd, że
A) 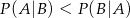 B)
B) 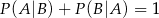
C) 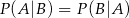 D)
D) 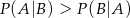
Zdarzenia losowe 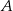 i
i 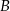 zawarte w
zawarte w 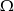 są takie, że prawdopodobieństwo
są takie, że prawdopodobieństwo 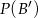 zdarzenia
zdarzenia 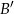 , przeciwnego do zdarzenia
, przeciwnego do zdarzenia 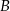 , jest równe
, jest równe 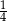 . Ponadto prawdopodobieństwo warunkowe
. Ponadto prawdopodobieństwo warunkowe 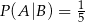 . Wynika stąd, że
. Wynika stąd, że
A) 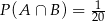 B)
B) 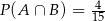 C)
C) 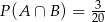 D)
D) 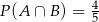
Zdarzenia losowe 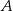 i
i 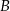 zawarte w
zawarte w 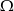 są takie, że prawdopodobieństwo
są takie, że prawdopodobieństwo 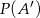 zdarzenia
zdarzenia 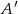 , przeciwnego do zdarzenia
, przeciwnego do zdarzenia 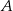 , jest równe
, jest równe  . Ponadto, prawdopodobieństwo warunkowe
. Ponadto, prawdopodobieństwo warunkowe 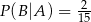 . Wynika stąd, że
. Wynika stąd, że
A) 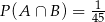 B)
B) 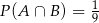 C)
C) 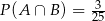 D)
D) 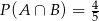
Jeżeli 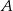 i
i 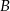 są zdarzeniami losowymi,
są zdarzeniami losowymi, 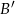 jest zdarzeniem przeciwnym do
jest zdarzeniem przeciwnym do 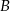 ,
, 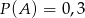 ,
, 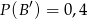 oraz
oraz 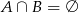 , to
, to 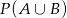 jest równe
jest równe
A) 0,12 B) 0,18 C) 0,6 D) 0,9
Jeżeli 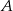 i
i 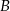 są zdarzeniami losowymi,
są zdarzeniami losowymi, 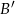 jest zdarzeniem przeciwnym do
jest zdarzeniem przeciwnym do 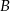 ,
, 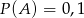 ,
, 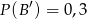 oraz
oraz 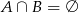 , to
, to 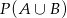 jest równe
jest równe
A) 0,4 B) 0,2 C) 0,8 D) 0,9
O zdarzeniach losowych 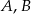 wiadomo, że:
wiadomo, że: 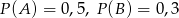 i
i 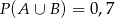 . Prawdopodobieństwo iloczynu zdarzeń
. Prawdopodobieństwo iloczynu zdarzeń 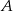 i
i 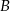 spełnia warunek
spełnia warunek
A) 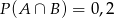 B)
B) 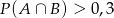 C)
C) 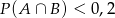 D)
D) 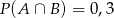
O zdarzeniach losowych 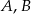 wiadomo, że:
wiadomo, że: 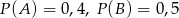 i
i 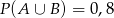 . Prawdopodobieństwo iloczynu zdarzeń
. Prawdopodobieństwo iloczynu zdarzeń 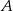 i
i 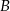 spełnia warunek
spełnia warunek
A) 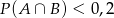 B)
B) 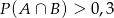 C)
C) 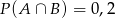 D)
D) 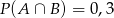
Wiadomo, że 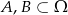 oraz
oraz 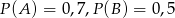 i
i 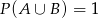 . Zatem
. Zatem
A) 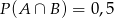 B)
B) 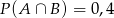 C)
C) 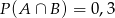 D)
D) 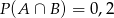
Wiadomo, że 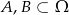 oraz
oraz 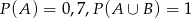 i
i 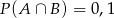 . Zatem
. Zatem
A) 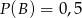 B)
B) 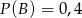 C)
C) 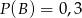 D)
D) 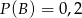
O zdarzeniach losowych 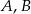 wiadomo, że:
wiadomo, że: 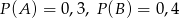 i
i 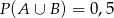 . Prawdopodobieństwo iloczynu zdarzeń
. Prawdopodobieństwo iloczynu zdarzeń 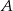 i
i 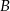 spełnia warunek
spełnia warunek
A)  B)
B) 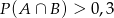 C)
C) 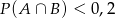 D)
D) 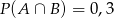
Wiadomo, że 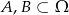 ,
, 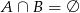 ,
, 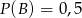 oraz
oraz 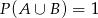 . Zatem
. Zatem
A) 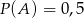 B)
B) 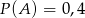 C)
C) 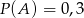 D)
D) 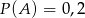
Zdarzenie 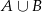 jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia
jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia 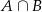 jest równe
jest równe 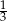 . Wobec tego suma prawdopodobieństw zdarzeń
. Wobec tego suma prawdopodobieństw zdarzeń 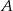 i
i 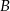 jest równa
jest równa
A) 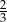 B)
B) 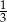 C) 1 D)
C) 1 D) 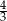
Zdarzenie 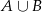 jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia
jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia 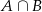 jest równe
jest równe 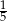 . Wobec tego suma prawdopodobieństw zdarzeń
. Wobec tego suma prawdopodobieństw zdarzeń 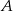 i
i 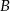 jest równa
jest równa
A) 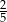 B)
B) 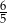 C) 1 D)
C) 1 D) 
Zdarzenia losowe 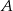 i
i 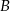 są rozłączne oraz
są rozłączne oraz 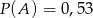 . Zatem prawdopodobieństwo zdarzenia
. Zatem prawdopodobieństwo zdarzenia 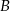 może być równe
może być równe
A) 0,63 B) 0,53 C) 0,43 D) 1
Zdarzenia losowe 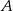 i
i 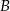 są rozłączne oraz
są rozłączne oraz 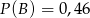 . Zatem prawdopodobieństwo zdarzenia
. Zatem prawdopodobieństwo zdarzenia 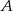 może być równe
może być równe
A) 0,63 B) 0,53 C) 0,73 D) 1
O zdarzeniach losowych 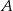 i
i 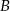 zawartych w
zawartych w 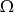 wiadomo, że
wiadomo, że 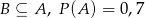 i
i 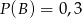 . Wtedy
. Wtedy
A) 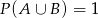 B)
B) 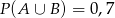 C)
C) 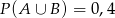 D)
D) 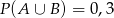
O zdarzeniach losowych 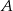 i
i 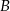 zawartych w
zawartych w 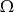 wiadomo, że
wiadomo, że 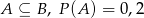 i
i 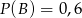 . Wtedy
. Wtedy
A) 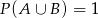 B)
B) 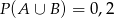 C)
C) 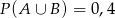 D)
D) 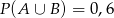
O zdarzeniach losowych 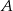 i
i 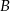 zawartych w
zawartych w 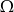 wiadomo, że
wiadomo, że 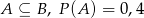 i
i 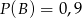 . Wtedy
. Wtedy
A) 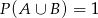 B)
B) 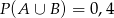 C)
C) 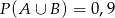 D)
D) 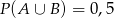
Niech 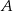 i
i 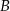 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 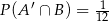 i
i 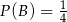 . Wtedy prawdopodobieństwo warunkowe
. Wtedy prawdopodobieństwo warunkowe 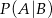 jest równe
jest równe
A) 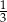 B)
B) 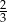 C)
C) 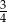 D)
D) 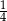
Niech 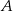 i
i 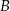 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 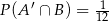 i
i 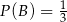 . Wtedy prawdopodobieństwo warunkowe
. Wtedy prawdopodobieństwo warunkowe 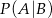 jest równe
jest równe
A) 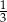 B)
B) 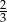 C)
C) 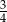 D)
D) 
Wiadomo, że 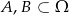 oraz
oraz 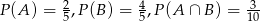 . Zatem:
. Zatem:
A) 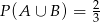 B)
B) 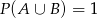 C)
C) 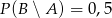 D)
D) 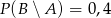
Wiadomo, że 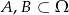 oraz
oraz 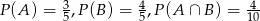 . Zatem:
. Zatem:
A) 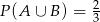 B)
B) 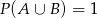 C)
C) 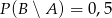 D)
D) 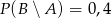
Zdarzenia 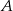 i
i 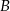 zawarte w zbiorze zdarzeń elementarnych
zawarte w zbiorze zdarzeń elementarnych 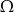 spełniają warunek
spełniają warunek 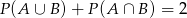 . Zatem
. Zatem
A) 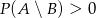 B)
B) 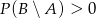 C)
C) 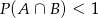 D)
D) 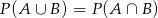
Zdarzenia 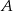 i
i 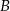 zawarte w zbiorze zdarzeń elementarnych
zawarte w zbiorze zdarzeń elementarnych 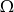 spełniają warunek
spełniają warunek 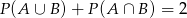 . Zatem
. Zatem
A) 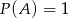 B)
B) 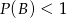 C)
C) 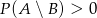 D)
D) 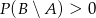
Prawdopodobieństwa zdarzeń 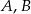 oraz zdarzeń przeciwnych
oraz zdarzeń przeciwnych 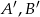 spełniają równości
spełniają równości 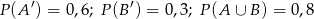 . Wtedy
. Wtedy 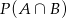 jest równe
jest równe
A) 0,5 B) 0,1 C) 0,3 D) 1
Prawdopodobieństwa zdarzeń 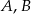 oraz zdarzeń przeciwnych
oraz zdarzeń przeciwnych 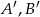 spełniają równości
spełniają równości 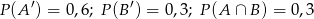 . Wtedy
. Wtedy 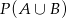 jest równe
jest równe
A) 0,6 B) 0,8 C) 0,3 D) 1
Prawdopodobieństwa zdarzeń 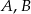 oraz zdarzeń przeciwnych
oraz zdarzeń przeciwnych 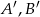 spełniają równości
spełniają równości 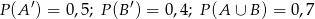 . Wtedy
. Wtedy 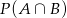 jest równe
jest równe
A) 0,4 B) 0,1 C) 0,3 D) 0,2
Niech 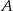 i
i 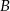 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 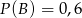 i
i 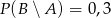 . Wtedy prawdopodobieństwo
. Wtedy prawdopodobieństwo 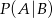 jest równe
jest równe
A) 0,3 B) 0,9 C) 0,5 D) 0,18
Niech 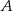 i
i 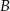 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 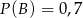 i
i 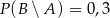 . Wtedy prawdopodobieństwo warunkowe
. Wtedy prawdopodobieństwo warunkowe 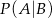 jest równe
jest równe
A) 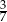 B)
B) 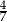 C)
C) 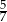 D)
D) 
Niech 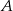 i
i 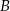 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 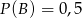 i
i 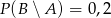 . Wtedy prawdopodobieństwo
. Wtedy prawdopodobieństwo 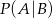 jest równe
jest równe
A) 0,3 B) 0,6 C) 0,5 D) 0,18
Prawdopodobieństwo zdarzenia 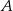 jest o 0,1 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do
jest o 0,1 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do 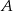 . Zatem
. Zatem 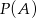 jest równe
jest równe
A) 0,6 B) 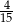 C) 0,4 D)
C) 0,4 D) 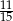
Dla pewnego zdarzenia losowego 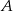 prawdziwe jest równanie (
prawdziwe jest równanie (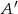 – zdarzenie przeciwne do zdarzenia
– zdarzenie przeciwne do zdarzenia 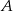 )
) 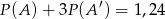 , zatem
, zatem
A) 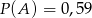 B)
B) 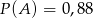 C)
C) 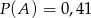 D)
D) 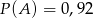
Prawdopodobieństwo zdarzenia 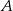 jest o 0,4 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do
jest o 0,4 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do 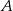 . Zatem
. Zatem 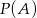 jest równe
jest równe
A) 0,6 B) 0,5 C) 0,4 D) 0,3
Dla pewnego zdarzenia losowego 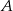 prawdziwe jest równanie (
prawdziwe jest równanie (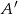 – zdarzenie przeciwne do zdarzenia
– zdarzenie przeciwne do zdarzenia 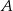 )
) 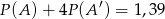 , zatem
, zatem
A) 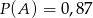 B)
B) 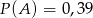 C)
C) 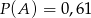 D)
D) 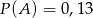
Prawdopodobieństwo zdarzenia 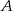 jest 6 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 6 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 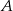 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 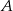 jest równe
jest równe
A) 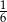 B)
B)  C)
C) 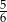 D)
D) 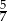
Prawdopodobieństwo zdarzenia 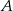 jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 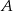 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 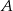 jest równe
jest równe
A) 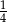 B)
B) 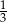 C)
C) 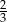 D)
D) 
Jeżeli prawdopodobieństwo zdarzenia losowego 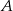 jest 5 razy większe od prawdopodobieństwa zdarzenia przeciwnego do zdarzenia
jest 5 razy większe od prawdopodobieństwa zdarzenia przeciwnego do zdarzenia 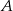 , to prawdopodobieństwo zdarzenia
, to prawdopodobieństwo zdarzenia 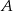 jest równe
jest równe
A) 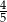 B)
B) 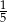 C)
C) 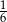 D)
D) 
Prawdopodobieństwo zdarzenia 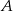 jest 7 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do
jest 7 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do 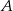 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 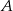 jest równe
jest równe
A)  B)
B)  C)
C) 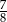 D)
D) 
Jeżeli 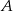 jest zdarzeniem losowym oraz
jest zdarzeniem losowym oraz 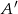 jest zdarzeniem przeciwnym do zdarzenia
jest zdarzeniem przeciwnym do zdarzenia 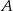 i
i 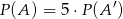 , to prawdopodobieństwo zdarzenia
, to prawdopodobieństwo zdarzenia 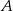 jest równe
jest równe
A) 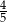 B)
B) 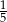 C)
C) 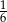 D)
D) 
Jeżeli 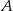 jest zdarzeniem losowym, a
jest zdarzeniem losowym, a 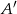 – zdarzeniem przeciwnym do zdarzenia
– zdarzeniem przeciwnym do zdarzenia 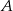 oraz zachodzi równość
oraz zachodzi równość 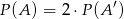 , to
, to
A) 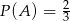 B)
B) 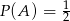 C)
C) 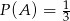 D)
D) 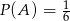
Prawdopodobieństwo zdarzenia 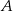 jest 5 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 5 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 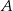 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 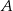 jest równe
jest równe
A)  B)
B) 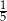 C)
C)  D)
D) 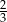
Prawdopodobieństwo zdarzenia 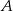 jest 6 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do
jest 6 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do 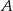 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 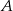 jest równe
jest równe
A) 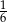 B)
B)  C)
C) 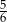 D)
D) 
O zdarzeniach losowych 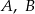 wiadomo, że:
wiadomo, że: 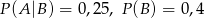 i
i 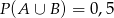 . Wtedy prawdopodobieństwo
. Wtedy prawdopodobieństwo 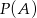 jest równe
jest równe
A) 0,1 B) 0,2 C) 0,3 D) 0,4

