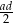Bok rombu tworzy z krótszą przekątną kąt o mierze 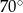 . Kąt ostry tego rombu ma miarę
. Kąt ostry tego rombu ma miarę
A) 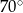 B)
B) 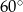 C)
C) 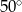 D)
D) 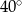
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Czworokąt
Bok rombu tworzy z krótszą przekątną kąt o mierze 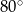 . Kąt ostry tego rombu ma miarę
. Kąt ostry tego rombu ma miarę
A) 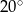 B)
B) 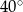 C)
C) 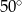 D)
D) 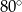
Przekątne dzielą równoległobok na cztery trójkąty
A) przystające B) podobne C) o równych polach D) o równych obwodach
W trapezie  (
(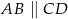 ) dłuższa podstawa ma długość
) dłuższa podstawa ma długość 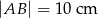 . Odcinek łączący środki ramion w tym trapezie ma długość 7 cm. Długość krótszej podstawy wynosi
. Odcinek łączący środki ramion w tym trapezie ma długość 7 cm. Długość krótszej podstawy wynosi
A) 5 cm B) 7 cm C) 4 cm D) 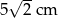
Punkty 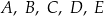 leżą na okręgu o środku
leżą na okręgu o środku 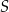 . Miara kąta
. Miara kąta 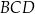 jest równa
jest równa 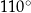 , a miara kąta
, a miara kąta 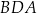 jest równa
jest równa 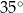 (zobacz rysunek).
(zobacz rysunek).

Wtedy kąt 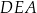 ma miarę równą
ma miarę równą
A) 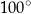 B)
B) 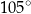 C)
C) 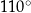 D)
D) 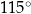
Bok rombu ma długość równą 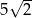 . Przekątne tego rombu nie mogą mieć długości
. Przekątne tego rombu nie mogą mieć długości
A) 14 i 2 B) 10 i 10 C) 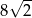 i
i 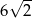 D)
D) 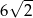 i
i 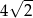
Krótszy bok prostokąta ma długość 6. Kąt między przekątną prostokąta i dłuższym bokiem ma miarę 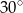 . Dłuższy bok prostokąta ma długość
. Dłuższy bok prostokąta ma długość
A) 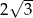 B)
B) 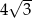 C)
C) 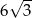 D) 12
D) 12
Dłuższy bok prostokąta ma długość 6. Kąt między przekątną prostokąta i dłuższym bokiem ma miarę 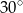 . Krótszy bok prostokąta ma długość
. Krótszy bok prostokąta ma długość
A) 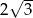 B)
B) 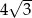 C)
C) 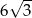 D) 12
D) 12
Odległości punktu 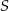 przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków
przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków 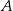 i
i 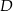 są równe
są równe 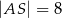 i
i 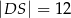 . Bok
. Bok 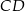 tego czworokąta ma długość
tego czworokąta ma długość
A) 27 B) 16 C) 24 D) 30
Pole rombu o obwodzie 8 jest równe 1. Kąt ostry tego rombu ma miarę  . Wtedy
. Wtedy
A)  B)
B)  C)
C) 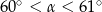 D)
D) 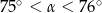
Pole rombu o obwodzie 40 jest równe 35. Kąt ostry tego rombu ma miarę  . Wtedy
. Wtedy
A) 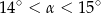 B)
B) 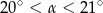 C)
C) 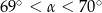 D)
D) 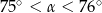
W równoległoboku 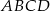 dłuższa podstawa ma długość
dłuższa podstawa ma długość 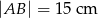 . Wysokości tego równoległoboku mają długości:
. Wysokości tego równoległoboku mają długości: 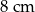 i
i 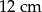 . Zatem krótsza podstawa równoległoboku ma długość
. Zatem krótsza podstawa równoległoboku ma długość
A) 20 cm B) 10 cm C) 3,2 cm D) 1,6 cm
O ile 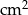 zwiększy się pole prostokąta o wymiarach
zwiększy się pole prostokąta o wymiarach  cm i
cm i 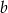 cm, jeżeli bok długości
cm, jeżeli bok długości  cm zwiększymy 2 razy, a bok długości
cm zwiększymy 2 razy, a bok długości 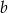 cm zwiększymy o 20%?
cm zwiększymy o 20%?
A) 2,4 B) 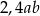 C)
C) 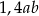 D) 1,4
D) 1,4
O ile 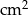 zwiększy się pole prostokąta o wymiarach
zwiększy się pole prostokąta o wymiarach 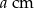 i
i 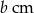 , jeżeli bok długości
, jeżeli bok długości 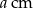 zwiększymy o 100%, a bok długości
zwiększymy o 100%, a bok długości 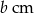 zwiększymy o 20%?
zwiększymy o 20%?
A) 2,4 B) 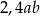 C)
C) 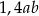 D) 1,4
D) 1,4
O ile 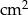 zwiększy się pole prostokąta o wymiarach
zwiększy się pole prostokąta o wymiarach 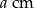 i
i 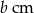 , jeżeli bok długości
, jeżeli bok długości  cm zwiększymy o 130%, a bok długości
cm zwiększymy o 130%, a bok długości 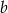 cm zwiększymy o 20%?
cm zwiększymy o 20%?
A) 2,76 B) 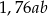 C)
C) 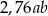 D) 1,76
D) 1,76
W trapezie 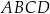 o podstawach
o podstawach 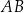 i
i 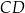 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 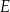 (zobacz rysunek).
(zobacz rysunek).
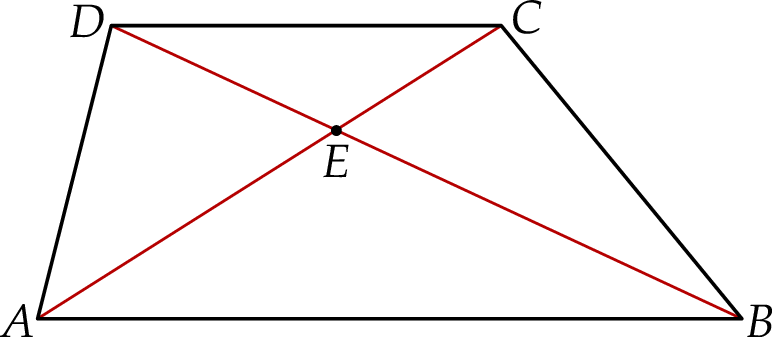
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 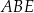 jest podobny do trójkąta jest podobny do trójkąta 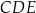 . . | P | F |
Pole trójkąta  jest równe polu trójkąta jest równe polu trójkąta 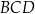 . . | P | F |
W trapezie 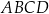 podstawa
podstawa 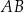 jest dłuższa od podstawy
jest dłuższa od podstawy 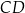 . Przekątne trapezu przecinają się w punkcie
. Przekątne trapezu przecinają się w punkcie 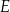 (zobacz rysunek).
(zobacz rysunek).
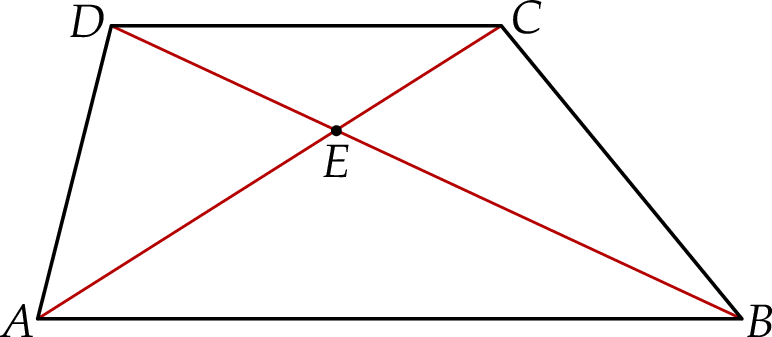
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta  jest równe polu trójkąta jest równe polu trójkąta  . . | P | F |
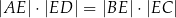 | P | F |
Przekątna 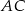 prostokąta
prostokąta 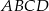 ma długość
ma długość 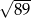 , a bok
, a bok 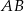 jest o 3 dłuższy od boku
jest o 3 dłuższy od boku 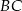 . Oblicz pole prostokąta.
. Oblicz pole prostokąta.
A) 8 B) 40 C) 5 D) 20
Jeden z boków równoległoboku ma długość równą 5. Przekątne tego równoległoboku mogą mieć długości
A) 4 i 6 B) 4 i 3 C) 10 i 10 D) 5 i 5
Jeden z boków równoległoboku ma długość równą 12. Przekątne tego równoległoboku mogą mieć długości
A) 10 i 10 B) 18 i 6 C) 12 i 12 D) 30 i 30
Przekątna kwadratu 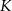 ma długość 2, a obwód kwadratu
ma długość 2, a obwód kwadratu 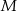 ma długość 16. Skala podobieństwa kwadratu
ma długość 16. Skala podobieństwa kwadratu 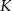 do kwadratu
do kwadratu 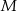 jest równa:
jest równa:
A) 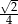 B)
B) 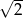 C) 4 D)
C) 4 D) 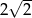
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 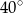 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 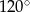 B)
B) 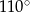 C)
C) 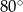 D)
D) 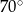
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 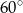 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 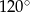 B)
B) 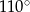 C)
C) 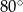 D)
D) 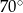
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 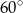 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 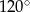 B)
B) 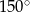 C)
C) 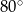 D)
D) 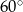
Pole równoległoboku o bokach długości 6 i 8 oraz kącie rozwartym 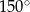 jest równe
jest równe
A) 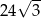 B) 48 C)
B) 48 C) 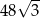 D) 24
D) 24
Boki równoległoboku mają długości 6 i 10, a kąt rozwarty między tymi bokami ma miarę 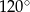 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 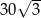 B) 30 C)
B) 30 C) 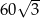 D) 60
D) 60
Pole równoległoboku o bokach długości 4 i 7 oraz kącie rozwartym 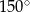 jest równe
jest równe
A) 14 B) 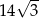 C)
C) 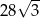 D) 28
D) 28
Pole równoległoboku o bokach długości 6 cm i 10 cm i kącie rozwartym o mierze 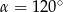 jest równe
jest równe
A) 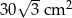 B)
B) 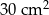 C)
C) 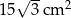 D)
D) 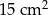
Dany jest równoległobok o bokach długości 3 i 4 oraz o kącie między nimi o mierze 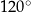 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 12 B) 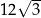 C) 6 D)
C) 6 D) 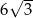
Różnica miar dwóch kątów rozwartych trapezu jest równa 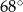 . Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
. Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
A) 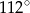 B)
B) 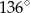 C)
C) 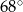 D)
D) 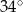
W trapezie prostokątnym kąt ostry ma miarę 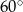 . Wysokość tego trapezu jest równa 3 cm. O ile centymetrów dłuższa jest jedna podstawa od drugiej?
. Wysokość tego trapezu jest równa 3 cm. O ile centymetrów dłuższa jest jedna podstawa od drugiej?
A) 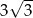 B) 6 C) 3 D)
B) 6 C) 3 D) 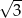
Przekątne trapezu 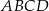 , w którym
, w którym 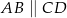 przecinają się w punkcie
przecinają się w punkcie 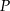 w ten sposób, że
w ten sposób, że 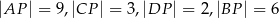 oraz
oraz 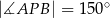 . Pole tego trapezu jest równe
. Pole tego trapezu jest równe
A) 32 B) 24 C) 18 D) 16
Dany jest romb o boku długości  i dłuższej przekątnej długości
i dłuższej przekątnej długości 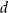 . Kąt rozwarty tego rombu ma miarę
. Kąt rozwarty tego rombu ma miarę 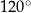 (zobacz rysunek).
(zobacz rysunek).
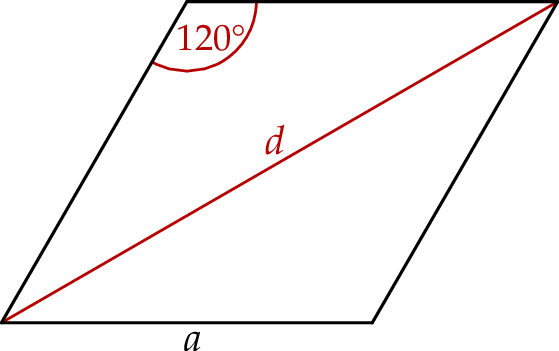
Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F. Pole tego rombu poprawnie określa wyrażenie
A) 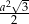 B)
B) 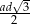 C)
C) 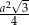
D) 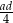 E)
E) 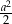 F)
F)