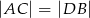Punkty 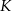 i
i 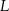 są punktami styczności okręgu wpisanego w trapez równoramienny
są punktami styczności okręgu wpisanego w trapez równoramienny  z bokami
z bokami 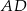 i
i 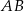 . Kąt ostry tego trapezu ma miarę
. Kąt ostry tego trapezu ma miarę 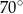 (zobacz rysunek).
(zobacz rysunek).
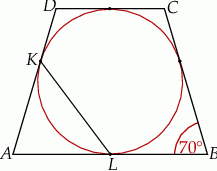
Miara kąta 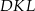 jest równa
jest równa
A) 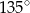 B)
B) 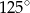 C)
C) 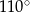 D)
D) 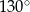
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 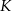 i
i 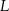 są punktami styczności okręgu wpisanego w trapez równoramienny
są punktami styczności okręgu wpisanego w trapez równoramienny  z bokami
z bokami 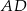 i
i 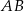 . Kąt ostry tego trapezu ma miarę
. Kąt ostry tego trapezu ma miarę 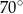 (zobacz rysunek).
(zobacz rysunek).

Miara kąta 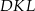 jest równa
jest równa
A) 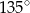 B)
B) 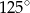 C)
C) 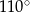 D)
D) 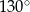
W trapezie  o podstawach
o podstawach  i
i  dane są:
dane są: 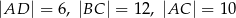 oraz
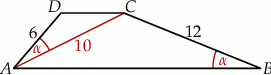
oraz 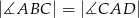 (zobacz rysunek).
(zobacz rysunek).
Wówczas długość podstawy 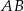 tego trapezu jest równa
tego trapezu jest równa
A) 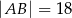 B)
B) 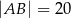 C)
C) 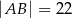 D)
D) 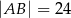
W trapezie  o podstawach
o podstawach 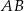 i
i 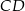 dane są:
dane są: 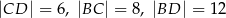 oraz
oraz 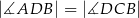 (zobacz rysunek).
(zobacz rysunek).
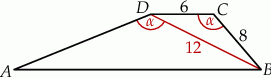
Wówczas długość ramienia  tego trapezu jest równa
tego trapezu jest równa
A)  B)
B)  C)
C) 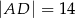 D)
D) 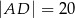
Kąty wewnętrzne przy wierzchołkach 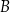 i
i 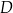 trapezu
trapezu 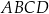 są równe odpowiednio
są równe odpowiednio 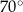 i
i 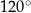 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 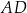 i
i 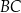 przecinają się pod kątem
przecinają się pod kątem
A) 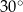 B)
B) 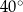 C)
C) 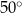 D)
D) 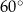
Kąty wewnętrzne przy wierzchołkach 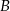 i
i 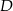 trapezu
trapezu 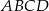 są równe odpowiednio
są równe odpowiednio 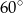 i
i 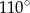 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 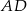 i
i 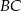 przecinają się pod kątem
przecinają się pod kątem
A) 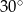 B)
B) 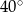 C)
C) 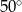 D)
D) 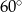
W trapezie prostokątnym krótsza podstawa i dłuższe ramię są równe i mają długość 8 cm. Kąt między dłuższym ramieniem i dłuższą podstawą ma miarę 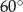 . Pole trapezu jest równe
. Pole trapezu jest równe
A) 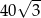 B)
B) 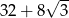 C) 40 D)
C) 40 D) 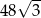
W trapezie prostokątnym podstawy mają długości 6 i 9. Która z liczb nie może być długością dłuższego ramienia trapezu?
A) 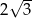 B)
B) 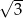 C)
C) 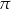 D)
D) 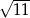
Przekątne trapezu 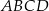 przecinają się w punkcie
przecinają się w punkcie  w ten sposób, że
w ten sposób, że 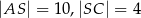 ,
, 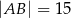 .
.
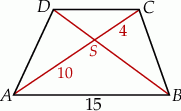
Długość odcinka 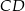 jest równa
jest równa
A) 4 B) 6 C) 8 D) 9
Z prostokąta 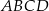 o polu 30 wycięto trójkąt
o polu 30 wycięto trójkąt 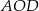 (tak jak na rysunku). Pole zacieniowanej figury jest równe
(tak jak na rysunku). Pole zacieniowanej figury jest równe
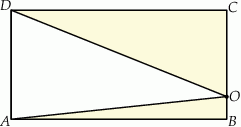
A) 7,5 B) 15 C) 20 D) 25
Z prostokąta 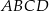 o polu 28 wycięto trójkąt
o polu 28 wycięto trójkąt 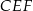 , przy czym punkty
, przy czym punkty 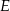 i
i 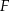 są środkami odpowiednio boków
są środkami odpowiednio boków 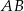 i
i 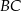 .
.
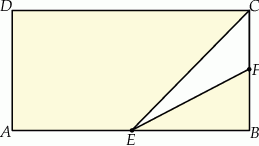
Pole zacieniowanej figury jest równe
A) 3,5 B) 21 C) 25 D) 24,5
Pole rombu o kącie ostrym 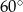 jest równe
jest równe 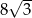 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 6 B) 2 C) 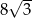 D) 4
D) 4
Pole rombu o kącie ostrym 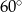 jest równe
jest równe 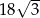 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 9 B) 3 C) 6 D) 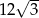
W trapezie prostokątnym kąt ostry ma miarę 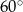 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
A) 6 B) 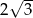 C)
C) 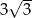 D)
D) 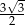
W trapezie prostokątnym kąt ostry ma miarę 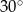 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
A) 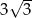 B)
B) 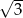 C) 6 D)
C) 6 D) 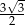
W trapezie prostokątnym kąt ostry ma miarę 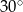 , a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa
, a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa
A) 4 B) 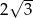 C)
C) 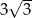 D)
D) 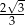
W trapezie prostokątnym kąt ostry ma miarę 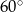 , a podstawy mają długości 10 i 8. Wysokość tego trapezu jest równa
, a podstawy mają długości 10 i 8. Wysokość tego trapezu jest równa
A) 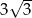 B) 4 C)
B) 4 C) 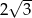 D)
D) 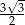
Bok rombu ma taką samą długość jak przekątna kwadratu. Pole rombu jest równe polu kwadratu. Zatem kąt ostry tego rombu ma miarę
A) 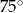 B)
B) 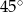 C)
C) 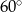 D)
D) 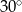
Przekątne podzieliły równoległobok na cztery trójkąty o polach 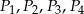 .
.
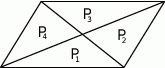
Który z podanych warunków może nie być spełniony?
A) 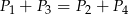 B)
B) 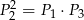 C)
C) 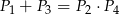 D)
D) 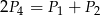
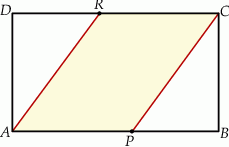
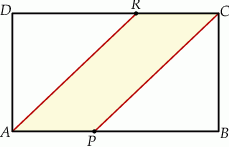
Pole prostokąta 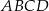 jest równe 90. Na bokach
jest równe 90. Na bokach 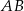 i
i 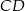 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 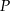 i
i 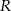 , takie, że
, takie, że 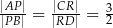 (zobacz rysunek)
(zobacz rysunek)
Pole czworokąta 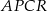 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Pole prostokąta 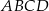 jest równe 90. Na bokach
jest równe 90. Na bokach 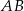 i
i 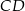 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 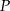 i
i 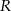 , takie, że
, takie, że 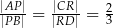 (zobacz rysunek)
(zobacz rysunek)
Pole czworokąta 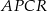 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Dany jest kwadrat o przekątnej 6. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 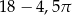 B)
B) 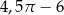 C)
C) 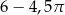 D)
D) 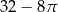
Dany jest kwadrat o przekątnej 2. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 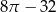 B)
B) 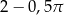 C)
C) 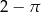 D)
D) 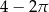
Dany jest kwadrat o przekątnej 4. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 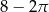 B)
B) 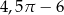 C)
C) 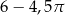 D)
D) 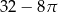
Stosunek boków prostokąta jest równy 1:2. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 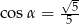 B)
B) 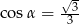 C)
C) 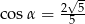 D)
D) 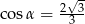
Stosunek boków prostokąta jest równy 2:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 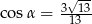 B)
B) 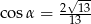 C)
C) 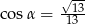 D)
D) 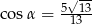
Stosunek boków prostokąta jest równy 1:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 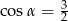 B)
B) 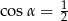 C)
C) 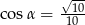 D)
D) 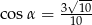
Stosunek boków prostokąta jest równy 1:2. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 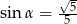 B)
B) 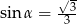 C)
C) 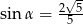 D)
D) 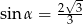
Stosunek boków prostokąta jest równy 2:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 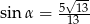 B)
B) 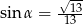 C)
C) 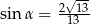 D)
D) 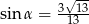
Miara kąta między bokiem 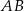 równoległoboku
równoległoboku 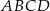 , a przekątną
, a przekątną 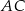 jest równa
jest równa 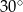 . Długość przekątnej
. Długość przekątnej 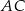 jest równa 5, a długość boku
jest równa 5, a długość boku 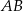 wynosi 4, zatem pole równoległoboku jest równe
wynosi 4, zatem pole równoległoboku jest równe
A) 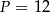 B)
B) 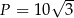 C)
C) 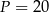 D)
D) 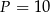
W kwadracie 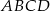 o boku długości 20 połączono punkty
o boku długości 20 połączono punkty 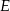 i
i 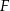 na bokach
na bokach 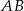 i
i 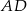 w ten sposób, że odcinek
w ten sposób, że odcinek 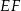 jest równoległy do przekątnej
jest równoległy do przekątnej 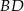 i jest od niej 5 razy krótszy.
i jest od niej 5 razy krótszy.
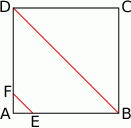
Długość odcinka 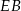 jest równa
jest równa
A) 12 B) 15 C) 14 D) 16
Wysokość rombu o boku długości 6 i kącie ostrym 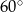 jest równa
jest równa
A) 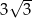 B) 3 C)
B) 3 C) 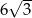 D) 6
D) 6
Wysokość rombu o boku długości 8 i kącie ostrym 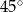 jest równa
jest równa
A) 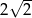 B) 4 C)
B) 4 C) 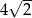 D) 8
D) 8
Przekątne trapezu 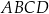 przecinają się w punkcie
przecinają się w punkcie  w ten sposób, że
w ten sposób, że 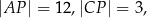
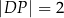 . Długość odcinka
. Długość odcinka 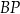 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
Przekątne trapezu 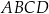 o podstawach
o podstawach 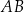 i
i 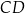 przecinają się w punkcie
przecinają się w punkcie 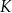 w ten sposób, że
w ten sposób, że 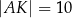 ,
, 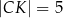 ,
, 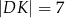 . Długość odcinka
. Długość odcinka 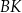 jest równa
jest równa
A) 7 B) 14 C) 10 D) 8
Przekątne trapezu 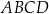 przecinają się w punkcie
przecinają się w punkcie 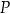 w ten sposób, że
w ten sposób, że 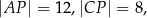
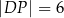 . Długość odcinka
. Długość odcinka 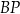 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
Przekątna równoległoboku dzieli go na dwa trójkąty równoramienne (zobacz rysunek).
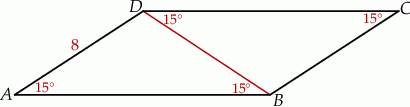
Pole tego równoległoboku jest równe
A) 16 B) 32 C) 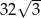 D)
D) 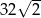
W równoległoboku 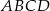 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 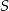 . Niech
. Niech 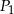 oznacza pole trójkąta
oznacza pole trójkąta 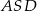 , natomiast
, natomiast 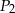 oznacza pole trójkąta
oznacza pole trójkąta 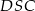 . Wówczas:
. Wówczas:
A) 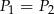 B)
B) 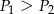 C)
C) 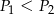 D)
D) 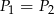 tylko wtedy, gdy
tylko wtedy, gdy 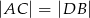
W równoległoboku 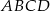 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 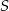 . Niech
. Niech 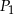 oznacza pole trójkąta
oznacza pole trójkąta 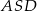 , natomiast
, natomiast 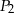 oznacza pole trójkąta
oznacza pole trójkąta 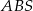 . Wówczas:
. Wówczas:
A) 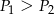 B)
B) 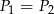 C)
C) 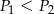 D)
D) 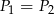 tylko wtedy, gdy
tylko wtedy, gdy