Na rysunku przedstawiono okrąg o środku 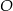 , który jest styczny do wszystkich boków trapezu równoramiennego
, który jest styczny do wszystkich boków trapezu równoramiennego 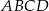 . Ramiona
. Ramiona 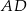 i
i 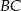 są styczne do tego okręgu odpowiednio w punktach
są styczne do tego okręgu odpowiednio w punktach 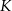 i
i 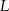 . Kąt wypukły
. Kąt wypukły 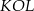 ma miarę
ma miarę 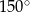 .
.
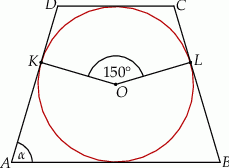
Miara  kąta ostrego tego trapezu jest równa
kąta ostrego tego trapezu jest równa
A) 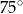 B)
B) 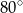 C)
C) 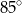 D)
D) 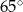

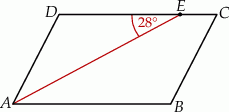
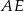 jest dwusieczną kąta
jest dwusieczną kąta 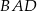 w równoległoboku
w równoległoboku 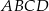 . Miara kąta
. Miara kąta 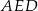 jest równa
jest równa 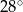 .
. 
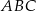 jest równa
jest równa 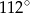
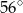
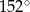
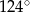
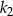 jest o 10% większa od długości boku kwadratu
jest o 10% większa od długości boku kwadratu 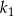 . Wówczas pole kwadratu
. Wówczas pole kwadratu 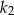 jest większe od pola kwadratu
jest większe od pola kwadratu 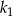 o
o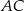 prostokąta
prostokąta 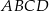 ma długość 70. Na boku
ma długość 70. Na boku 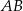 obrano punkt
obrano punkt 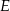 , na przekątnej
, na przekątnej 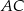 obrano punkt
obrano punkt 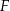 , a na boku
, a na boku 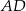 obrano punkt
obrano punkt 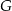 – tak, że czworokąt
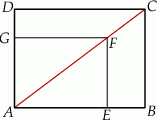
– tak, że czworokąt 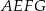 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 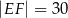 i
i 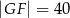 .
. 
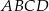 jest równy
jest równy 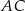 prostokąta
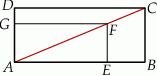
prostokąta 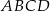 ma długość 104. Na boku
ma długość 104. Na boku 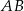 obrano punkt
obrano punkt 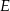 , na przekątnej
, na przekątnej 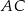 obrano punkt
obrano punkt 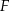 , a na boku
, a na boku 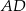 obrano punkt
obrano punkt 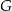 – tak, że czworokąt
– tak, że czworokąt 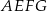 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 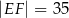 i
i 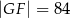 .
. 
 jest równy
jest równy  , w którym przekątna
, w którym przekątna  jest prostopadła do ramienia
jest prostopadła do ramienia 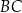 ,
, 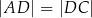 oraz
oraz 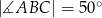 (zobacz rysunek).
(zobacz rysunek). 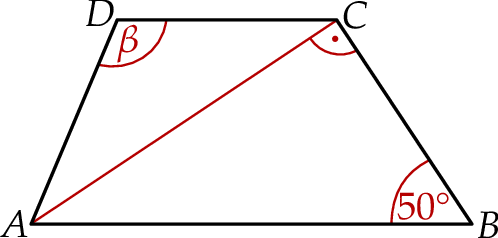
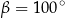
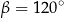
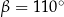
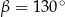
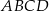 , w którym przekątna
, w którym przekątna 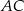 jest prostopadła do ramienia
jest prostopadła do ramienia 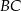 ,
, 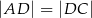 oraz
oraz 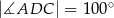 (zobacz rysunek).
(zobacz rysunek). 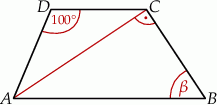
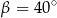
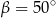
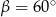
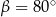
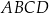 , w którym bok
, w którym bok 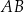 jest równoległy do boku
jest równoległy do boku 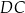 . W tym trapezie poprowadzono odcinek
. W tym trapezie poprowadzono odcinek 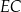 równoległy do boku
równoległy do boku 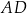 , podano miary dwóch kątów oraz oznaczono kąt
, podano miary dwóch kątów oraz oznaczono kąt  (zobacz rysunek).
(zobacz rysunek). 
 ma miarę
ma miarę 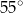
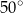
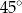
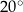
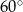 wpisano okrąg. Promień tego okręgu jest równy
wpisano okrąg. Promień tego okręgu jest równy 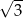
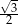
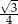
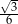
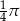
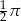
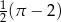
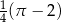
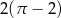
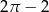
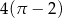
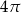
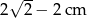
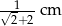
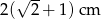
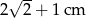
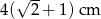
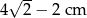
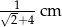
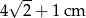
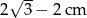
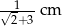
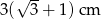
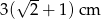
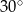 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe 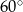 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe 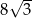
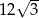
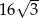
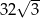
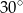 . Krótszy bok prostokąta ma długość
. Krótszy bok prostokąta ma długość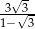
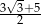
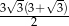
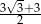
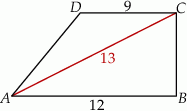
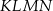 , którego podstawy mają długości
, którego podstawy mają długości 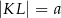 ,
, 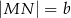 ,
, 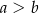 . Kąt
. Kąt 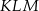 ma miarę
ma miarę 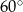 . Długość ramienia
. Długość ramienia 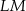 tego trapezu jest równa
tego trapezu jest równa 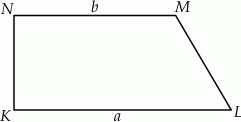
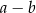
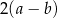
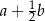
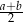
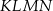 , którego podstawy mają długości
, którego podstawy mają długości 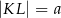 ,
, 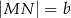 ,
, 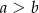 . Kąt
. Kąt 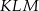 ma miarę
ma miarę 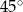 . Długość ramienia
. Długość ramienia 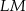 tego trapezu jest równa
tego trapezu jest równa 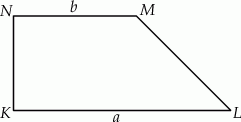
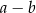
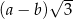
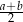
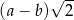
 i kącie
i kącie 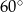 wpisano okrąg. Promień tego okręgu jest równy
wpisano okrąg. Promień tego okręgu jest równy 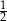


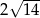
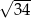
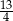
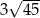
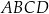 podzielono przekątną
podzielono przekątną 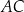 na dwa trójkąty. Punkty
na dwa trójkąty. Punkty 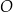 i
i 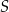 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty 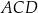 i
i 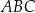 , a odcinek
, a odcinek 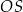 przecina przekątną
przecina przekątną 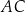 w punkcie
w punkcie 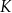 (zobacz rysunek). Stosunek długości okręgów o środkach
(zobacz rysunek). Stosunek długości okręgów o środkach 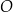 i
i 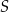 jest równy
jest równy  , a odcinek
, a odcinek 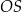 ma długość 24.
ma długość 24. 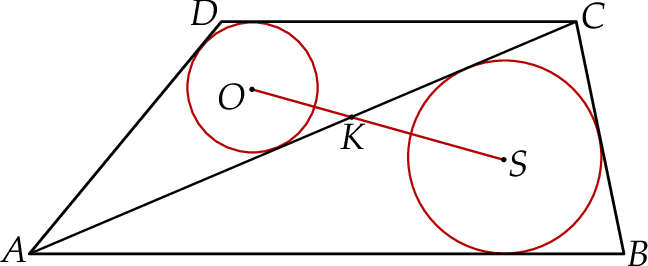
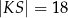
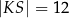
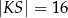
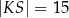
 , takim, że
, takim, że 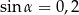 . Długość przekątnej tego prostokąta jest równa
. Długość przekątnej tego prostokąta jest równa 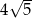
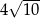
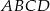 (
(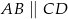 ) wysokość
) wysokość 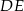 podzieliła podstawę na odcinki długości
podzieliła podstawę na odcinki długości 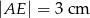 i
i 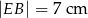 . Odcinek łączący środki ramion w tym trapezie ma długość
. Odcinek łączący środki ramion w tym trapezie ma długość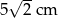
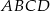 (
(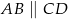 ) wysokość
) wysokość 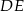 podzieliła podstawę na odcinki długości
podzieliła podstawę na odcinki długości 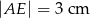 i
i 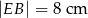 . Odcinek łączący środki ramion w tym trapezie ma długość
. Odcinek łączący środki ramion w tym trapezie ma długość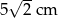
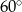 i ramieniu długości
i ramieniu długości 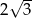 jest równa
jest równa 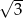
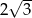
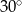 i ramieniu długości
i ramieniu długości 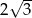 jest równa
jest równa 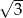
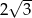
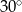 i ramieniu długości
i ramieniu długości 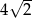 jest równa
jest równa 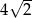
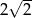
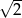
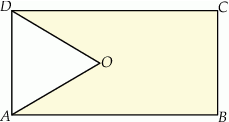
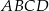 o obwodzie 30 wycięto trójkąt równoboczny
o obwodzie 30 wycięto trójkąt równoboczny 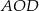 o obwodzie 15 (tak jak na rysunku).
o obwodzie 15 (tak jak na rysunku).