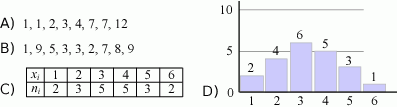
Dla której z przedstawionych serii danych mediana jest równa 3?
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dla której z przedstawionych serii danych mediana jest równa 3?

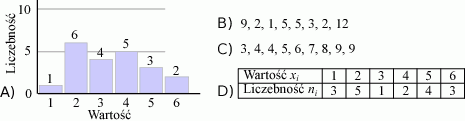
Dla której z przedstawionych serii danych mediana jest równa 4?
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
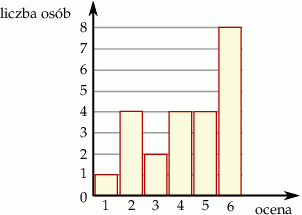
Mediana ocen uzyskanych przez uczniów jest równa
A) 6 B) 5 C) 4,5 D) 4
Przeprowadzono badanie dotyczące liczby samochodów osobowych w rodzinie. Wyniki przedstawia poniższy diagram
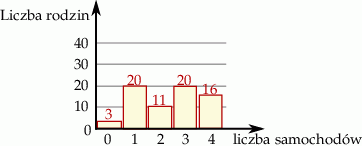
Mediana liczby samochodów w rodzinie wynosi
A) 2 B) 2,5 C) 3 D) 3,5
Poniższy diagram przedstawia wiek uczestników pewnej wycieczki.
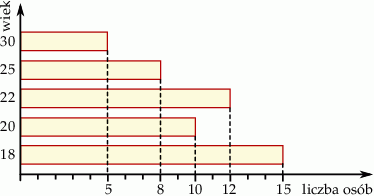
Mediana wieku osób uczestniczących w tej wycieczce jest równa:
A) 21 lat B) 21,68 lat C) 22 lata D) 23 lata
Firma  zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy 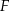 , którzy otrzymują płacę miesięczną w danej wysokości.
, którzy otrzymują płacę miesięczną w danej wysokości.
Mediana miesięcznej płacy pracowników firmy  jest równa
jest równa
A) 4 000 zł B) 4 800 zł C) 5 000 zł D) 5 500 zł
Poniższy diagram przedstawia wiek uczestników pewnej wycieczki.
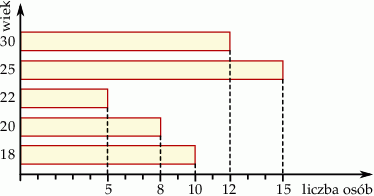
Mediana wieku osób uczestniczących w tej wycieczce jest równa:
A) 21 lat B) 22 lata C) 23,5 lat D) 25 lat
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
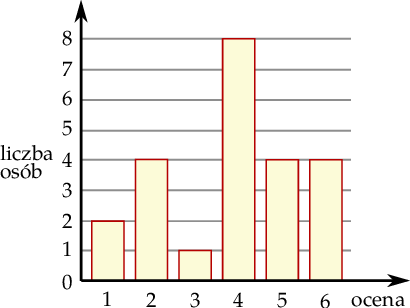
Mediana ocen uzyskanych przez uczniów jest równa
A) 3,5 B) 5 C) 4,5 D) 4
Na diagramie podano wzrost uczniów klasy I w pewnym liceum.
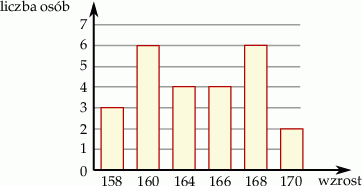
Mediana wszystkich wyników jest równa
A) 163 B) 164 C) 165 D) 166
Przeprowadzono badanie dotyczące liczby samochodów osobowych w rodzinie. Wyniki przedstawia poniższy diagram
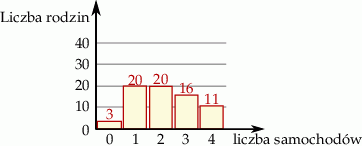
Mediana liczby samochodów w rodzinie wynosi
A) 2 B) 2,5 C) 3 D) 3,5
Na diagramie przedstawiono wyniki sprawdzianu z matematyki w pewnej klasie maturalnej. Na osi poziomej podano oceny, które uzyskali uczniowie tej klasy, a na osi pionowej podano liczbę uczniów, którzy otrzymali daną ocenę.
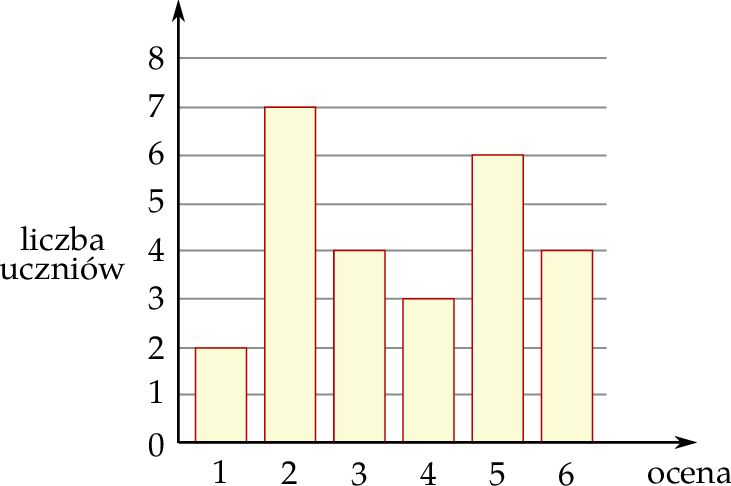
Mediana ocen uzyskanych z tego sprawdzianu przez uczniów tej klasy jest równa
A) 4,5 B) 4 C) 3,5 D) 3
Średnia arytmetyczna zestawu danych:
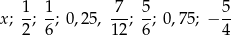
jest równa 0,25. Wtedy mediana tego zestawu danych jest równa
A) 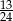 B)
B) 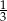 C)
C)  D)
D) 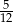
Mediana danych 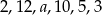 jest równa 7. Wówczas
jest równa 7. Wówczas
A) 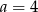 B)
B) 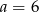 C)
C) 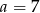 D)
D) 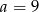
Mediana danych 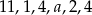 jest równa 3. Wówczas
jest równa 3. Wówczas
A) 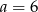 B)
B) 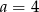 C)
C) 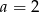 D)
D) 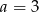
Mediana zestawu sześciu danych liczb: 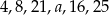 jest równa 14. Zatem
jest równa 14. Zatem
A) 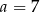 B)
B) 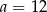 C)
C) 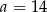 D)
D) 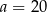
Mediana danych 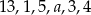 jest równa 4. Wówczas
jest równa 4. Wówczas
A) 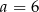 B)
B) 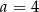 C)
C) 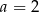 D)
D) 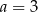
Medianą zestawu danych  jest liczba 4. Wtedy
jest liczba 4. Wtedy  może być równe
może być równe
A) 2 B) 3 C) 4 D) 5
Medianą zestawu danych 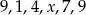 jest liczba 8. Wtedy
jest liczba 8. Wtedy  może być równe
może być równe
A) 8 B) 4 C) 7 D) 9
Mediana zestawu ośmiu danych liczb: 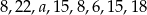 jest równa 14. Zatem
jest równa 14. Zatem
A) 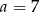 B)
B) 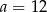 C)
C) 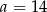 D)
D) 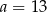
Sześć liczb: 19, 15, 13,  , 7, 1, tworzących zestaw danych, jest uporządkowanych malejąco. Mediana tego zestawu sześciu danych jest równa medianie zestawu pięciu danych: 15,
, 7, 1, tworzących zestaw danych, jest uporządkowanych malejąco. Mediana tego zestawu sześciu danych jest równa medianie zestawu pięciu danych: 15,  , 8, 2, 19. Zatem
, 8, 2, 19. Zatem
A) 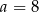 B)
B) 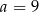 C)
C) 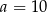 D)
D) 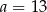
Firma  zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy 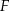 , którzy otrzymują płacę miesięczną w danej wysokości.
, którzy otrzymują płacę miesięczną w danej wysokości.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Mediana miesięcznej płacy pracowników firmy  jest równa 4800 zł. jest równa 4800 zł. | P | F |
| Ponad 78% pracowników tej firmy zarabia nie więcej niż 5000 zł brutto. | P | F |
Średnia arytmetyczna zestawu danych: 3, 8, 3, 11, 3, 10, 3,  jest równa 6. Mediana tego zestawu jest równa
jest równa 6. Mediana tego zestawu jest równa
A) 5 B) 6 C) 7 D) 8
Średnia arytmetyczna zestawu danych:  , 2, 4, 6, 8, 10, 12, 14 jest równa 9. Wtedy mediana tego zestawu danych jest równa
, 2, 4, 6, 8, 10, 12, 14 jest równa 9. Wtedy mediana tego zestawu danych jest równa
A) 8 B) 9 C) 10 D) 16
Średnia arytmetyczna zestawu danych: 4, 5, 3, 8, 10, 4, 8, 9, 6,  jest równa 6,5. Mediana tego zestawu jest równa
jest równa 6,5. Mediana tego zestawu jest równa
A) 5 B) 6 C) 7 D) 8
Średnia arytmetyczna zestawu danych:  , 2, 4, 6, 8, 10, 13, 16 jest równa 8,5. Wtedy mediana tego zestawu danych jest równa
, 2, 4, 6, 8, 10, 13, 16 jest równa 8,5. Wtedy mediana tego zestawu danych jest równa
A) 8 B) 8,5 C) 9 D) 10
Średnia arytmetyczna liczb:  , 13, 7, 5, 5, 3, 2, 11 jest równa 7. Mediana tego zestawu liczb jest równa
, 13, 7, 5, 5, 3, 2, 11 jest równa 7. Mediana tego zestawu liczb jest równa
A) 6 B) 7 C) 10 D) 5
Średnia arytmetyczna sześciu liczb naturalnych: 21, 14, 19, 15, 24,  , jest równa
, jest równa 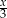 . Mediana tych liczb jest równa
. Mediana tych liczb jest równa
A) 17 B) 20 C) 19 D) 21
Średnia arytmetyczna liczb: 3, 1, 6, 5, 2, 4,  , 2, 3, 8 wynosi 4. Medianą tego zbioru liczb jest
, 2, 3, 8 wynosi 4. Medianą tego zbioru liczb jest
A) 3,5 B) 3 C) 4,5 D) 4
Średnia arytmetyczna sześciu liczb naturalnych: 31, 16, 25, 29, 27,  , jest równa
, jest równa 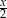 . Mediana tych liczb jest równa
. Mediana tych liczb jest równa
A) 26 B) 27 C) 28 D) 29
Mediana danych zawartych w tabeli liczebności jest równa 3.
| Wartość | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczebność | 3 | 4 |  | 1 | 2 | 6 |
Zatem  może być równe
może być równe
A) 0 B) 1 C) 2 D) 3
W tabeli poniżej przedstawione są wyniki pracy klasowej w dwóch klasach pierwszych.
| Ocena | 3,25 | 2,75 | 4,25 | 4 | 2 | 5,25 | 3,75 | 4,75 | 1 | 3 | 5 | 2,25 | 6 | 5,75 |
| Liczba ocen | 2 | 5 | 2 | 1 | 5 | 1 | 3 | 2 | 1 | 4 | 3 | 1 | 2 | 3 |
Mediana ocen w tych dwóch klasach jest równa
A) 4 B) 3 C) 3,25 D) 3,75
Średnia arytmetyczna dziesięciu kolejnych liczb naturalnych jest równa 15,5. Mediana tych liczb jest równa
A) 15,5 B) 31 C) 16 D) 16,5
Cztery liczby: 2, 3,  , 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
A) 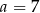 B)
B) 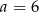 C)
C) 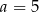 D)
D) 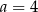
Cztery liczby: 2, 3,  , 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 7, 2, 4, 9, 1. Zatem
, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 7, 2, 4, 9, 1. Zatem
A) 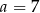 B)
B) 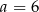 C)
C) 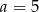 D)
D) 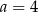
Ze zbioru liczb 3, 4, 1, 5, 1, 3, 1 usunięto jedną liczbę w ten sposób, że mediana tego zbioru liczb nie uległa zmianie. Usunięta liczba to
A) 1 B) 3 C) 4 D) 5
