Objętość kuli o promieniu 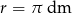 jest równa
jest równa
A) 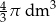 B)
B) 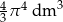 C)
C) 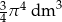 D)
D) 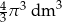
/Szkoła średnia
Objętość kuli o promieniu 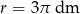 jest równa
jest równa
A) 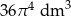 B)
B) 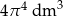 C)
C) 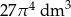 D)
D) 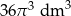
Jacek i Karol rzucają śnieżkami do celu. Jacek trafia do celu średnio trzy razy na dziesięć rzutów, a Karol trafia do celu średnio raz na pięć rzutów. Prawdopodobieństwo, że cel zostanie trafiony dokładnie raz, jeżeli każdy z chłopców wykona po jednym rzucie jest równe
A) 0,06 B) 0,38 C) 0,56 D) 0,5
Ewa i Kasia rzucają śnieżkami do celu. Ewa trafia do celu średnio raz na pięć rzutów, a Kasia trafia do celu średnio trzy razy na dziesięć rzutów. Prawdopodobieństwo, że cel zostanie trafiony dokładnie raz, jeżeli każda z dziewcząt wykona po jednym rzucie jest równe
A) 0,5 B) 0,56 C) 0,38 D) 0,06
Oblicz pole powierzchni całkowitej i objętość prostopadłościanu 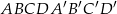 , w którym krawędź
, w którym krawędź 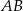 ma długość 10 cm i tworzy z przekątną
ma długość 10 cm i tworzy z przekątną 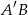 ściany bocznej kąt
ściany bocznej kąt 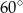 , a krawędź
, a krawędź 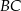 jest o cztery centymetry krótsza od krawędzi
jest o cztery centymetry krótsza od krawędzi 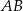 .
.
Liczba 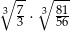 jest równa
jest równa
A) 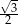 B)
B) 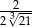 C)
C)  D)
D) 
Liczba 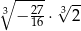 jest równa
jest równa
A) 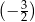 B)
B)  C)
C)  D)
D) 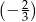
Wartość wyrażenia 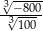 jest równa
jest równa
A) 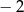 B)
B) 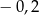 C) 2 D) 0,2
C) 2 D) 0,2
Liczba 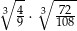 jest równa
jest równa
A)  B)
B) 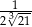 C)
C) 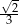 D)
D) 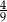
Liczba 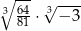 jest równa
jest równa
A) 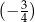 B)
B) 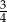 C)
C) 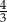 D)
D) 
Liczba 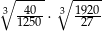 jest równa
jest równa
A) 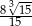 B)
B) 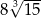 C) 8 D)
C) 8 D) 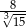
Podstawą ostrosłupa 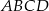 jest trójkąt równoramienny o podstawie
jest trójkąt równoramienny o podstawie 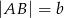 i kącie
i kącie  pomiędzy ramionami. Krawędź
pomiędzy ramionami. Krawędź 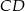 jest wysokością ostrosłupa, a kąt nachylenia ściany
jest wysokością ostrosłupa, a kąt nachylenia ściany 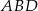 do podstawy ostrosłupa jest równy
do podstawy ostrosłupa jest równy 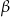 . Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Podaj wymiary prostokąta, którego boki różnią się o 6 cm, a przekątna ma długość 30 cm.
Para liczb 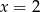 i
i 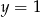 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 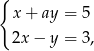 gdy
gdy
A) 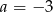 B)
B) 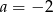 C)
C) 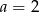 D)
D) 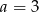
Para liczb 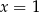 ,
, 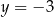 spełnia układ równań
spełnia układ równań
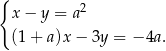
Wtedy  jest równe
jest równe
A) 2 B) 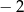 C)
C) 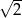 D)
D) 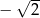
Para liczb 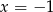 i
i 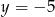 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 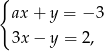 gdy
gdy
A) 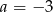 B)
B) 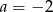 C)
C) 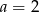 D)
D) 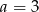
Para liczb 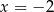 i
i 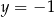 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 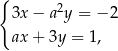 dla
dla
A) 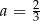 B)
B) 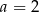 C)
C) 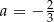 D)
D) 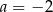
Para liczb 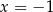 i
i 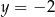 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 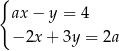 dla
dla
A) 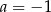 B)
B) 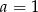 C)
C) 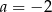 D)
D) 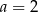
Para liczb 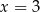 i
i 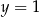 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 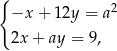 dla
dla
A) 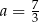 B)
B) 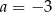 C)
C) 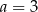 D)
D) 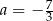
Para liczb 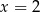 i
i 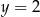 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 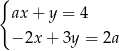 dla
dla
A) 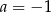 B)
B) 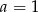 C)
C) 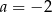 D)
D) 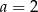
Para liczb 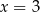 ,
, 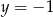 spełnia układ równań
spełnia układ równań
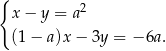
Wtedy  jest równe
jest równe
A) 2 B) 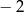 C)
C) 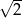 D)
D) 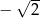
Zależność między temperaturą wyrażoną w stopniach Fahrenheita, a wyrażoną w stopniach Celsjusza jest zależnością liniową.
- Znajdź tę zależność wiedząc ze
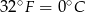 , a
, a 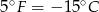 .
. - 22 lipca w San Diego temperatura o godzinie
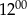 była o
była o 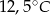 wyższa niż temperatura o godzinie
wyższa niż temperatura o godzinie 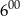 . Wyraź wzrost temperatury w stopniach Fahrenheita.
. Wyraź wzrost temperatury w stopniach Fahrenheita.
Dla jakich wartości parametru 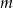 równanie
równanie ![3 2 2 (x + 3x − 4)[(m − 5 )x + (m − 2)x − 1 ] = 0](https://img.zadania.info/zad/9801521/HzadT1x.gif) ma cztery różne pierwiastki?
ma cztery różne pierwiastki?
Do naczynia w kształcie odwróconego stożka wrzucono kulkę o promieniu 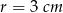 . Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.
. Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.
Wyznacz największy wyraz ciągu 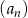 danego wzorem
danego wzorem 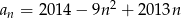 , dla
, dla 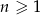 .
.
Pochodna funkcji 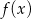 jest równa
jest równa 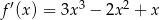 . Funkcja
. Funkcja 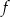 może mieć wzór
może mieć wzór
A) 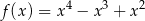 B)
B) 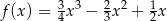
C) 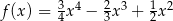 D)
D) 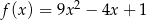
Ciągiem Fibonacciego nazywamy ciąg, którego dwa pierwsze wyrazy są równe 1, a każdy kolejny jest sumą dwóch poprzednich. Jaką liczbą, parzystą czy nieparzystą, jest 528 wyraz ciągu Fibonacciego? Odpowiedź uzasadnij.
Funkcja 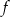 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 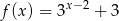 . Prosta
. Prosta 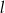 ma równanie
ma równanie 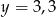 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 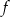 i prosta
i prosta 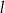 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Funkcja 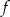 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 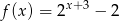 . Prosta
. Prosta 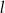 ma równanie
ma równanie 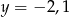 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 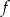 i prosta
i prosta 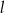 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Wyznacz 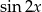 i
i 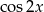 jeśli wiadomo że
jeśli wiadomo że 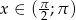 i
i 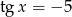 .
.
Wyznacz 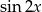 i
i 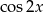 jeśli wiadomo, że
jeśli wiadomo, że 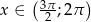 i
i 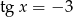 .
.
Oblicz szerokość prostokątnej ramy obrazu wiedząc, że obwód zewnętrzny ramy jest o 28 cm większy od obwodu wewnętrznego tej ramy.
W urnie jest pewna liczba kul białych i jedna kula czarna. Losujemy jedną kulę z tej urny, zatrzymujemy ją, a następnie z pozostałych kul losujemy jedną kulę. Ile powinno być kul białych w urnie, aby prawdopodobieństwo wylosowania dwóch kul białych było równe 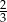 ?
?
Wyznacz dziedzinę funkcji określonej wzorem 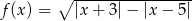 .
.
Z talii 52 kart losujemy jednocześnie dwie karty. Oblicz prawdopodobieństwo, że przynajmniej jedna z nich będzie starsza od 10, jeśli wiadomo, że żadna z nich nie jest karem.
Prosta 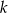 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 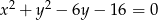 . Odległość środka tego okręgu od prostej
. Odległość środka tego okręgu od prostej 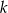 jest równa
jest równa
A) 9 B) 4 C) 25 D) 5
Prosta 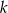 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 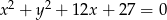 . Odległość środka tego okręgu od prostej
. Odległość środka tego okręgu od prostej 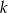 jest równa
jest równa
A) 9 B) 3 C) 25 D) 5

