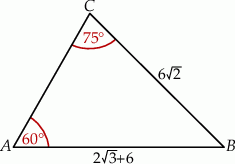
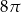Pole trójkąta 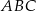 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
A) 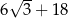 B)
B) 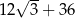 C)
C) 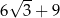 D)
D) 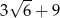
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Pole trójkąta 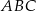 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe

A) 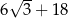 B)
B) 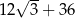 C)
C) 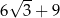 D)
D) 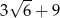
Narysuj dowolny trapez, a potem wykreśl trójkąt o takim samym polu.
Każdej karcie bankomatowej jest przypisany numer identyfikacyjny zwany kodem PIN. Kod ten składa się z czterech cyfr (cyfry mogą się powtarzać, ale kodem PIN nie może być 0000). Oblicz prawdopodobieństwo, że w losowo utworzonym kodzie PIN żadna cyfra się nie powtórzy. Wynik podaj w postaci ułamka nieskracalnego.
Wykaż, że jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 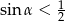 to
to 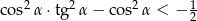 .
.
Liczba 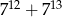 jest podzielna przez
jest podzielna przez
A) 16 B) 6 C) 4 D) 5
Liczba 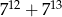 nie jest podzielna przez
nie jest podzielna przez
A) 14 B) 7 C) 8 D) 5
Dane są zbiory liczb całkowitych: 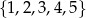 i
i 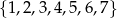 . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
. Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
Dane są dwa zbiory: 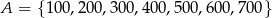 i
i 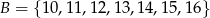 . Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3. Obliczone prawdopodobieństwo zapisz w postaci nieskracalnego ułamka zwykłego.
. Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3. Obliczone prawdopodobieństwo zapisz w postaci nieskracalnego ułamka zwykłego.
Dane są dwa zbiory:
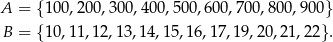
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 9.
Dane są zbiory liczb całkowitych: 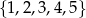 i
i 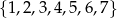 . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 7.
. Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 7.
Liczba 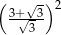 jest równa
jest równa
A) 4 B) 9 C) 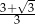 D)
D) 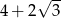
Liczba 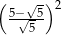 jest równa
jest równa
A) 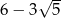 B) 4 C)
B) 4 C) 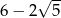 D) 6
D) 6
Liczba 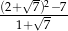 jest równa
jest równa
A) 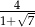 B) 4 C)
B) 4 C) 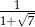 D) 2
D) 2
Liczba 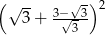 jest równa
jest równa
A) 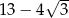 B) 11 C)
B) 11 C) 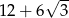 D) 3
D) 3
W trapez wpisano okrąg. Punkt styczności okręgu z dłuższą podstawą trapezu dzieli tę podstawę na odcinki długości 2,5 dm i 4 dm. Wysokość trapezu ma długość 4 dm. Oblicz obwód tego trapezu.
Liczba -7 jest miejscem zerowym 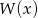 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 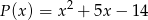 , jeśli wiadomo, że w wyniku dzielenia wielomianu
, jeśli wiadomo, że w wyniku dzielenia wielomianu 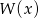 przez dwumian
przez dwumian 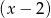 otrzymujemy resztę 18.
otrzymujemy resztę 18.
W kartezjańskim układzie współrzędnych 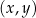 prosta
prosta 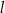 o równaniu
o równaniu 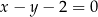 przecina parabolę o równaniu
przecina parabolę o równaniu 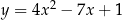 w punktach
w punktach 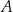 oraz
oraz 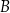 . Odcinek
. Odcinek 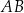 jest średnicą okręgu
jest średnicą okręgu 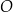 . Punkt
. Punkt 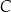 leży na okręgu
leży na okręgu 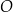 nad prostą
nad prostą 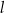 , a kąt
, a kąt 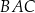 jest ostry i ma miarę
jest ostry i ma miarę  taką, że
taką, że 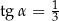 (zobacz rysunek).
(zobacz rysunek).
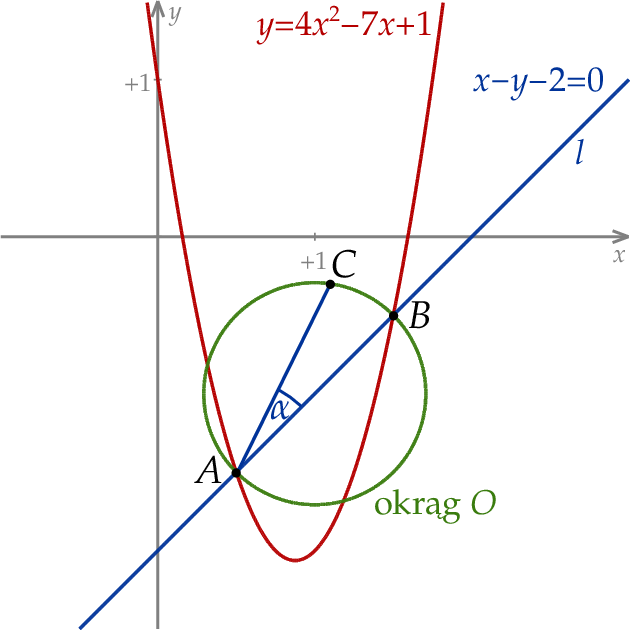
Oblicz współrzędne punktu 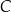 .
.
W kartezjańskim układzie współrzędnych 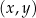 prosta
prosta 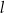 o równaniu
o równaniu 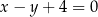 przecina parabolę o równaniu
przecina parabolę o równaniu 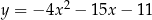 w punktach
w punktach 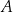 oraz
oraz 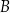 . Odcinek
. Odcinek 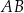 jest średnicą okręgu
jest średnicą okręgu 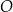 . Punkt
. Punkt 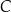 leży na okręgu
leży na okręgu 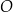 poniżej prostej
poniżej prostej 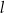 , a kąt
, a kąt 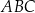 jest ostry i ma miarę
jest ostry i ma miarę  taką, że
taką, że 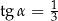 (zobacz rysunek).
(zobacz rysunek).
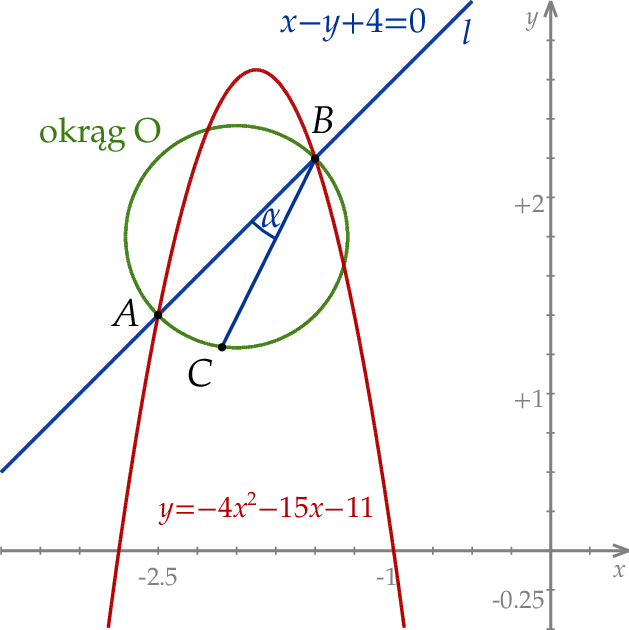
Oblicz współrzędne punktu 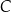 .
.
Ośmiościan foremny jest bryłą zbudowaną z ośmiu przystających trójkątów równobocznych (zobacz rysunek).
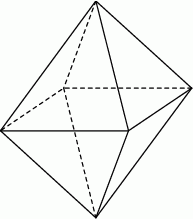
Oblicz objętość i pole powierzchni ośmiościanu foremnego, którego krawędź ma długość 6 cm.
W układzie współrzędnych dane są punkty 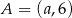 oraz
oraz 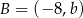 . Punkt
. Punkt 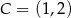 jest takim punktem odcinka
jest takim punktem odcinka  , że
, że 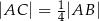 . Wynika stąd, że
. Wynika stąd, że
A) 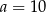 i
i 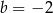 B)
B) 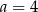 i
i 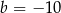 C)
C) 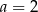 i
i 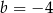 D)
D) 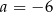 i
i 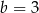
Funkcja 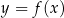 jest określona za pomocą tabeli
jest określona za pomocą tabeli
 | 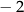 | 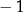 | 0 | 1 | 2 |
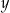 | 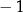 | 0 | 1 | 0 | 3 |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 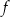 ma dokładnie jedno miejsce zerowe. ma dokładnie jedno miejsce zerowe. | P | F |
Wykres funkcji 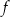 jest symetryczny względem osi jest symetryczny względem osi 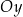 . . | P | F |
Funkcja 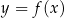 jest określona za pomocą tabeli
jest określona za pomocą tabeli
 | 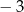 | 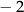 | 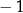 | 0 | 1 | 2 | 3 |
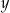 | 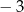 | 2 | 0 | 1 | 0 | 2 | 1 |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 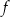 ma dokładnie jedno miejsce zerowe. ma dokładnie jedno miejsce zerowe. | P | F |
W kartezjańskim układzie współrzędnych 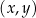 wykres funkcji wykres funkcji 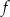 jest symetryczny względem osi jest symetryczny względem osi 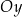 . . | P | F |
Największa wartość funkcji 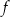 jest równa 3. jest równa 3. | P | F |
Uzasadnij, że kąt ostry między dwusiecznymi kątów ostrych trójkąta prostokątnego jest równy 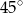 .
.
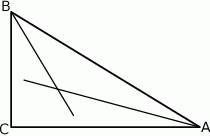
Dany jest kwadrat o przekątnej 6. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 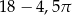 B)
B) 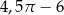 C)
C) 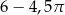 D)
D) 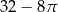
Dany jest kwadrat o przekątnej 2. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 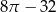 B)
B) 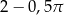 C)
C) 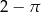 D)
D) 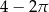
Dany jest kwadrat o przekątnej 4. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 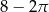 B)
B) 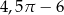 C)
C) 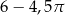 D)
D) 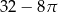
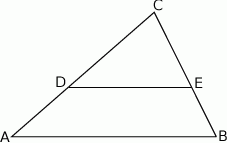
Pole trójkąta 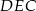 wynosi
wynosi 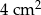 . Wiadomo, że
. Wiadomo, że 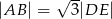 oraz
oraz 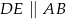 . Zatem pole trójkąta
. Zatem pole trójkąta 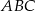 jest równe
jest równe
A) 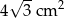 B)
B) 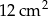 C)
C) 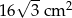 D)
D) 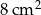
Suma długości dwóch boków trójkąta równa się 4, a kąt między tymi bokami ma miarę 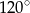 . Oblicz najmniejszą wartość sumy kwadratów długości wszystkich boków tego trójkąta.
. Oblicz najmniejszą wartość sumy kwadratów długości wszystkich boków tego trójkąta.
Rozwiąż nierówność 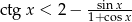 , gdzie
, gdzie 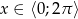 ;
;
Prosta 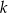 przecina oś
przecina oś 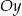 układu współrzędnych w punkcie
układu współrzędnych w punkcie 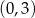 i jest prostopadła do prostej o równaniu
i jest prostopadła do prostej o równaniu 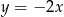 . Wówczas prosta
. Wówczas prosta 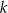 przecina oś
przecina oś 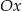 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 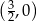 B)
B) 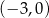 C)
C) 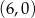 D)
D) 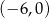
Przekątna przekroju osiowego walca jest o 13 dłuższa od promienia podstawy tego walca, oraz o 2 dłuższa od jego wysokości. Pole podstawy tego walca jest równe
A) 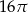 B)
B) 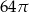 C)
C) 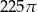 D)
D)