Do naczynia w kształcie odwróconego stożka wrzucono kulkę o promieniu 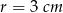 . Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.
. Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.
/Szkoła średnia
Wyznacz największy wyraz ciągu 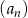 danego wzorem
danego wzorem 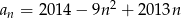 , dla
, dla 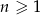 .
.
Pochodna funkcji 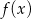 jest równa
jest równa 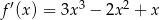 . Funkcja
. Funkcja 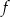 może mieć wzór
może mieć wzór
A) 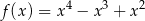 B)
B) 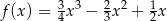
C) 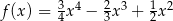 D)
D) 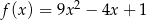
Ciągiem Fibonacciego nazywamy ciąg, którego dwa pierwsze wyrazy są równe 1, a każdy kolejny jest sumą dwóch poprzednich. Jaką liczbą, parzystą czy nieparzystą, jest 528 wyraz ciągu Fibonacciego? Odpowiedź uzasadnij.
Funkcja 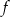 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 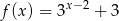 . Prosta
. Prosta 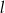 ma równanie
ma równanie 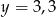 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 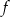 i prosta
i prosta 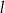 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Funkcja 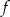 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 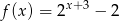 . Prosta
. Prosta 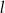 ma równanie
ma równanie 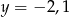 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 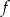 i prosta
i prosta 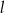 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Wyznacz 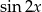 i
i 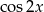 jeśli wiadomo że
jeśli wiadomo że 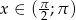 i
i 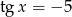 .
.
Wyznacz 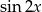 i
i 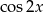 jeśli wiadomo, że
jeśli wiadomo, że 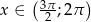 i
i 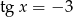 .
.
Oblicz szerokość prostokątnej ramy obrazu wiedząc, że obwód zewnętrzny ramy jest o 28 cm większy od obwodu wewnętrznego tej ramy.
W urnie jest pewna liczba kul białych i jedna kula czarna. Losujemy jedną kulę z tej urny, zatrzymujemy ją, a następnie z pozostałych kul losujemy jedną kulę. Ile powinno być kul białych w urnie, aby prawdopodobieństwo wylosowania dwóch kul białych było równe 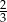 ?
?
Wyznacz dziedzinę funkcji określonej wzorem 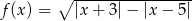 .
.
Z talii 52 kart losujemy jednocześnie dwie karty. Oblicz prawdopodobieństwo, że przynajmniej jedna z nich będzie starsza od 10, jeśli wiadomo, że żadna z nich nie jest karem.
Prosta 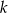 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 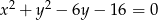 . Odległość środka tego okręgu od prostej
. Odległość środka tego okręgu od prostej 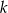 jest równa
jest równa
A) 9 B) 4 C) 25 D) 5
Prosta 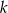 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 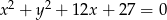 . Odległość środka tego okręgu od prostej
. Odległość środka tego okręgu od prostej 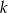 jest równa
jest równa
A) 9 B) 3 C) 25 D) 5
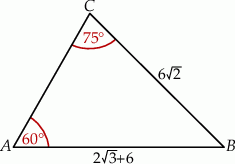
Pole trójkąta 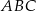 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
A) 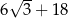 B)
B) 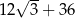 C)
C) 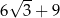 D)
D) 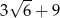
Narysuj dowolny trapez, a potem wykreśl trójkąt o takim samym polu.
Każdej karcie bankomatowej jest przypisany numer identyfikacyjny zwany kodem PIN. Kod ten składa się z czterech cyfr (cyfry mogą się powtarzać, ale kodem PIN nie może być 0000). Oblicz prawdopodobieństwo, że w losowo utworzonym kodzie PIN żadna cyfra się nie powtórzy. Wynik podaj w postaci ułamka nieskracalnego.
Wykaż, że jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 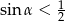 to
to 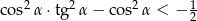 .
.
Liczba 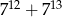 jest podzielna przez
jest podzielna przez
A) 16 B) 6 C) 4 D) 5
Liczba 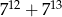 nie jest podzielna przez
nie jest podzielna przez
A) 14 B) 7 C) 8 D) 5
Dane są zbiory liczb całkowitych: 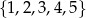 i
i 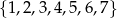 . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
. Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
Dane są dwa zbiory: 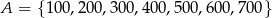 i
i 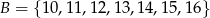 . Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3. Obliczone prawdopodobieństwo zapisz w postaci nieskracalnego ułamka zwykłego.
. Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3. Obliczone prawdopodobieństwo zapisz w postaci nieskracalnego ułamka zwykłego.
Dane są dwa zbiory:
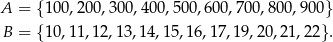
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 9.
Dane są zbiory liczb całkowitych: 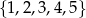 i
i 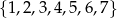 . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 7.
. Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 7.
Liczba 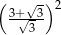 jest równa
jest równa
A) 4 B) 9 C) 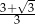 D)
D) 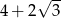
Liczba 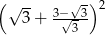 jest równa
jest równa
A) 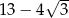 B) 11 C)
B) 11 C) 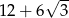 D) 3
D) 3
Liczba 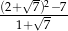 jest równa
jest równa
A) 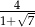 B) 4 C)
B) 4 C) 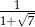 D) 2
D) 2
Liczba 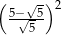 jest równa
jest równa
A) 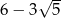 B) 4 C)
B) 4 C) 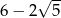 D) 6
D) 6
W trapez wpisano okrąg. Punkt styczności okręgu z dłuższą podstawą trapezu dzieli tę podstawę na odcinki długości 2,5 dm i 4 dm. Wysokość trapezu ma długość 4 dm. Oblicz obwód tego trapezu.
Liczba -7 jest miejscem zerowym 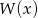 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 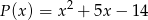 , jeśli wiadomo, że w wyniku dzielenia wielomianu
, jeśli wiadomo, że w wyniku dzielenia wielomianu 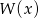 przez dwumian
przez dwumian 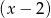 otrzymujemy resztę 18.
otrzymujemy resztę 18.

