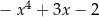Suma dwóch wielomianów, z których każdy jest stopnia piątego, może być wielomianem stopnia
A) drugiego B) szóstego C) dziesiątego D) dwudziestego piątego
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany/Dwa wielomiany/Suma i różnica
Który z wielomianów należy dodać do wielomianu 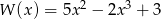 aby otrzymać wielomian
aby otrzymać wielomian 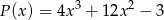 ?
?
A) 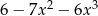 B)
B) 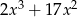 C)
C) 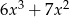 D)
D) 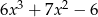
Wielomian 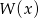 jest sumą wielomianów
jest sumą wielomianów 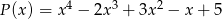 i
i 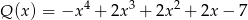 . Zatem stopień wielomianu
. Zatem stopień wielomianu 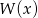 jest równy
jest równy
A) 16 B) 8 C) 4 D) 2
Wielomian 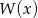 jest sumą wielomianów
jest sumą wielomianów 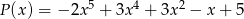 i
i 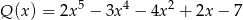 . Zatem stopień wielomianu
. Zatem stopień wielomianu 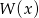 jest równy
jest równy
A) 2 B) 4 C) 5 D) 10
Dane są wielomiany 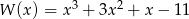 i
i 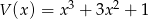 . Stopień wielomianu
. Stopień wielomianu 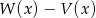 jest równy
jest równy
A) 0 B) 1 C) 2 D) 3
Dane są wielomiany 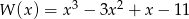 i
i 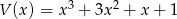 . Stopień wielomianu
. Stopień wielomianu 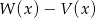 jest równy
jest równy
A) 0 B) 1 C) 2 D) 3
Wielomiany 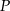 i
i 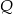 określone są wzorami
określone są wzorami 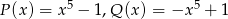 . Wielomian
. Wielomian 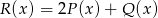 jest stopnia
jest stopnia
A) 0 B) 10 C) 1 D) 5
Wielomiany 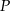 i
i 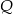 określone są wzorami
określone są wzorami 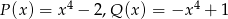 . Wielomian
. Wielomian 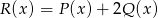 jest stopnia
jest stopnia
A) 0 B) 4 C) 2 D) 8
Wielomiany 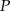 i
i 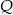 określone są wzorami
określone są wzorami 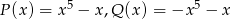 . Wielomian
. Wielomian 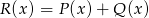 jest stopnia
jest stopnia
A) 0 B) 10 C) 1 D) 5
Dane są wielomiany 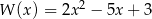 i
i 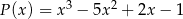 . Wielomian
. Wielomian 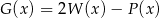 jest równy
jest równy
A) 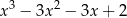 B)
B) 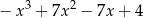
C) 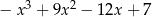 D)
D) 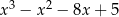
Dane są wielomiany 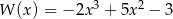 oraz
oraz 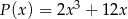 . Wielomian
. Wielomian 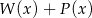 jest równy
jest równy
A) 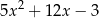 B)
B) 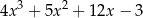
C) 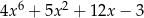 D)
D) 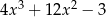
Dane są wielomiany 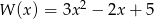 oraz
oraz 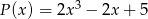 . Wielomian
. Wielomian 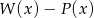 jest równy
jest równy
A) 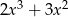 B)
B) 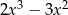 C)
C) 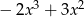 D)
D) 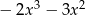
Dane są wielomiany 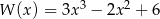 oraz
oraz 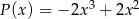 . Wielomian
. Wielomian 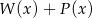 jest równy
jest równy
A) 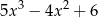 B)
B) 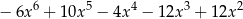
C) 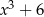 D)
D) 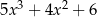
Dane są wielomiany 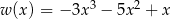 i
i 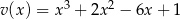 . Wówczas wielomian
. Wówczas wielomian 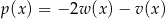 jest równy:
jest równy:
A) 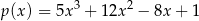 B)
B) 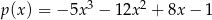
C) 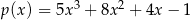 D)
D) 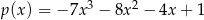
Dane są wielomiany 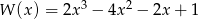 i
i 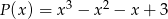 . Wielomian
. Wielomian 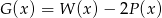 jest równy
jest równy
A) 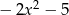 B)
B) 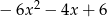 C)
C) 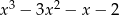 D)
D) 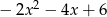
Dane są wielomiany 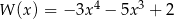 oraz
oraz 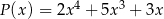 . Wielomian
. Wielomian 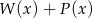 jest równy
jest równy
A) 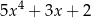 B)
B) 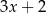
C) 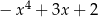 D)
D)