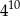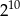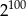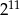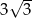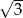W równoległoboku 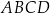 bok
bok 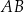 jest dwa razy dłuższy od boku
jest dwa razy dłuższy od boku 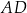 . Punkt
. Punkt 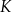 jest środkiem boku
jest środkiem boku 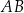 , a punkt
, a punkt 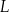 jest środkiem boku
jest środkiem boku  .
.
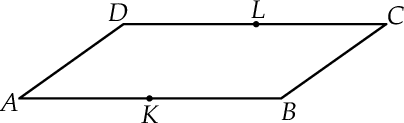
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 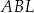 ma takie samo pole, jak trójkąt ma takie samo pole, jak trójkąt 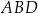 . . | P | F |
Pole równoległoboku 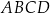 jest cztery razy większe od pola trójkąta jest cztery razy większe od pola trójkąta 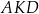 . . | P | F |

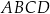 bok
bok 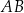 jest dwa razy dłuższy od boku
jest dwa razy dłuższy od boku 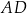 . Punkt
. Punkt 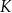 jest środkiem boku
jest środkiem boku 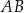 , a punkt
, a punkt 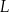 jest środkiem boku
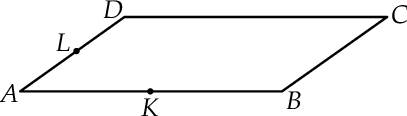
jest środkiem boku 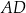 .
. 
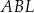 ma takie samo pole, jak trójkąt
ma takie samo pole, jak trójkąt 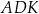 .
. 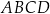 jest cztery razy większe od pola trójkąta
jest cztery razy większe od pola trójkąta 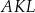 .
.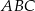 o obwodzie 50 wycięto kwadrat
o obwodzie 50 wycięto kwadrat 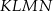 o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy 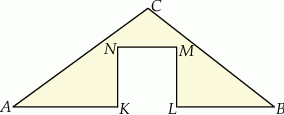
 wpisano trójkąt równoboczny tak jak przedstawiono na rysunku.
wpisano trójkąt równoboczny tak jak przedstawiono na rysunku. 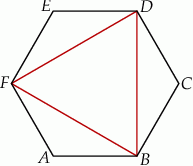
 jest większy niż 80% obwodu sześciokąta
jest większy niż 80% obwodu sześciokąta 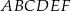 .
.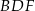 jest 3 razy większe od pola trójkąta
jest 3 razy większe od pola trójkąta 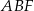 .
. 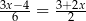
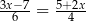
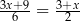
 ), a czasem ich druku w sekundach (
), a czasem ich druku w sekundach (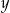 ), jeżeli tempo drukowania biletów nie ulega zmianie?
), jeżeli tempo drukowania biletów nie ulega zmianie? 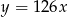
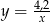
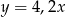
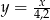
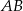 podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części (
podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części ( ), na którą dzielimy odcinek
), na którą dzielimy odcinek 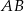 , a długością (
, a długością (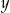 ) jednej takiej części w milimetrach?
) jednej takiej części w milimetrach? 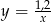
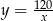
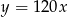
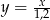
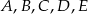 są środkami jej krawędzi.
są środkami jej krawędzi. 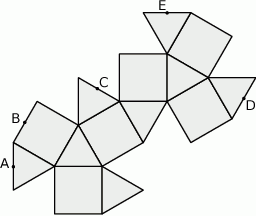
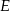 pokryje się z punktem
pokryje się z punktem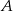
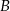
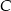
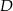
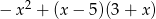 można przekształcić do postaci
można przekształcić do postaci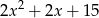
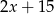
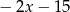
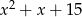
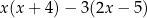 można przekształcić równoważnie do postaci
można przekształcić równoważnie do postaci 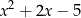
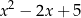
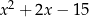
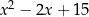
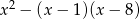 można przekształcić do postaci
można przekształcić do postaci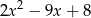
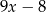
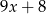
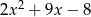
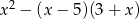 można przekształcić do postaci
można przekształcić do postaci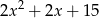
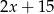
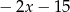
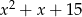
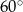 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa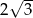
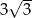
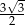
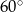 , a podstawy mają długości 10 i 8. Wysokość tego trapezu jest równa
, a podstawy mają długości 10 i 8. Wysokość tego trapezu jest równa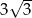
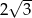
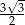
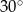 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa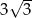
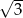
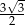
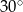 , a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa
, a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa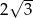
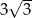
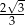
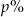 . Wynika stąd, że
. Wynika stąd, że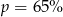
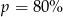
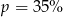
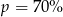
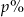 . Wynika stąd, że
. Wynika stąd, że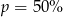
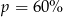
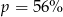
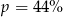
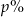 . Wynika stąd, że
. Wynika stąd, że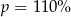
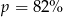
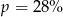
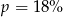
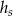 i walec o wysokości
i walec o wysokości 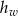 mają takie same podstawy o polu
mają takie same podstawy o polu 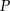 . Stożek ma dwa razy większą objętość niż walec, czyli
. Stożek ma dwa razy większą objętość niż walec, czyli 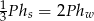 .
.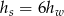
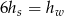
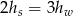
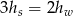
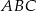 mają miary
mają miary 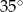 i
i 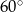 . Trójkąt podobny do trójkąta
. Trójkąt podobny do trójkąta 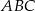 może mieć kąty o miarach
może mieć kąty o miarach 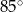 i
i 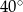
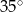 i
i 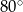
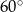 i
i 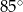
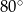 i
i 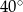
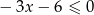
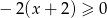
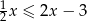
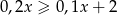
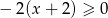
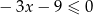
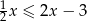
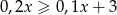
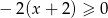
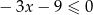
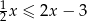
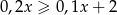
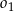 w symetrii względem punktu
w symetrii względem punktu 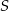 jest okrąg
jest okrąg 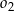 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 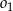 i
i 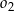 mają dwa punkty wspólne, to
mają dwa punkty wspólne, to 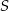 leży na zewnątrz koła ograniczonego okręgiem
leży na zewnątrz koła ograniczonego okręgiem 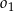 .
. 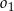 i
i 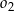 mają jeden punkt wspólny, to
mają jeden punkt wspólny, to 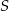 jest punktem okręgu
jest punktem okręgu 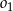 .
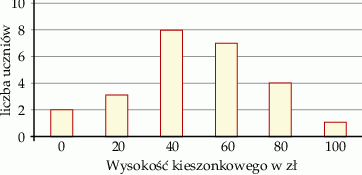
. 
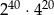 jest równa
jest równa 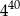
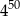
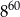
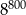
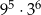 jest równa
jest równa 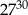
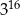
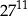
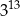
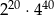 jest równa
jest równa 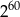
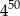
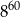
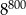
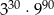 jest równa
jest równa 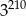
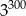
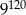
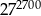
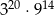 jest równa
jest równa 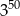
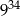
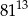
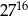
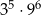 jest równa
jest równa 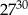
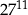
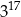
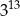
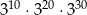 jest równa
jest równa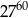
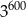
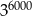
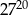
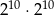 jest równa.
jest równa.