Podstawą ostrosłupa prawidłowego trójkątnego 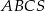 jest trójkąt równoboczny
jest trójkąt równoboczny 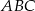 . Wysokość
. Wysokość 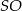 tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 27. Oblicz pole powierzchni bocznej ostrosłupa
tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 27. Oblicz pole powierzchni bocznej ostrosłupa 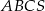 oraz cosinus kąta, jaki tworzą wysokość ściany bocznej i płaszczyzna podstawy ostrosłupa.
oraz cosinus kąta, jaki tworzą wysokość ściany bocznej i płaszczyzna podstawy ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny/Różne
Wysokość ostrosłupa prawidłowego trójkątnego jest dwa razy krótsza od promienia okręgu opisanego na podstawie tego ostrosłupa, a jego objętość jest równa 9. Oblicz pole powierzchni bocznej ostrosłupa oraz tangens kąta, jaki tworzy krawędź boczna z krawędzią podstawy ostrosłupa.
Podstawą ostrosłupa prawidłowego trójkątnego 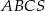 jest trójkąt równoboczny
jest trójkąt równoboczny 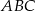 . Wysokość
. Wysokość 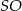 tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 8. Oblicz sumę długości wszystkich krawędzi ostrosłupa
tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 8. Oblicz sumę długości wszystkich krawędzi ostrosłupa 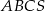 oraz cosinus kąta, jaki tworzą krawędź boczna i płaszczyzna podstawy ostrosłupa.
oraz cosinus kąta, jaki tworzą krawędź boczna i płaszczyzna podstawy ostrosłupa.
Objętość ostrosłupa prawidłowego trójkątnego jest równa 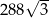 . Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze
. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
taki, że 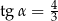 .
.
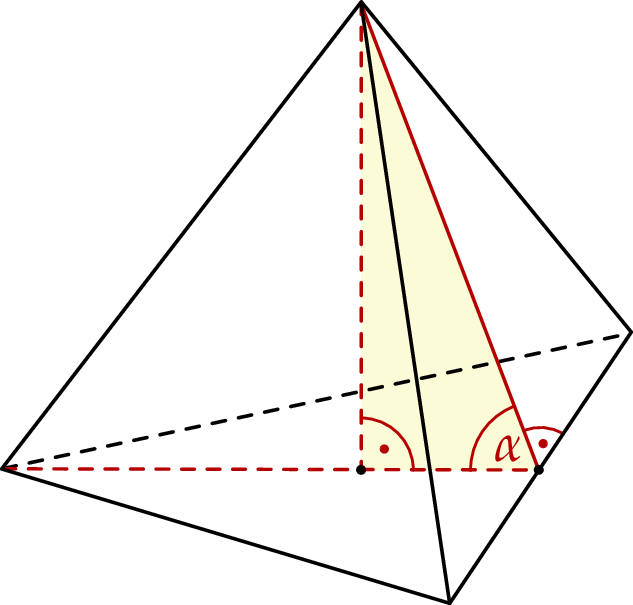
Oblicz wysokość ściany bocznej tego ostrosłupa.
W sferę o promieniu 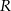 wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość
wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość 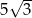 , oblicz
, oblicz 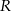 .
.
Każda z krawędzi podstawy trójkątnej ostrosłupa ma długość 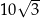 , a każda jego krawędź boczna ma długość 15. Oblicz wysokość tego ostrosłupa.
, a każda jego krawędź boczna ma długość 15. Oblicz wysokość tego ostrosłupa.
Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego jest równe 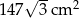 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 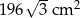 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa.
Krawędź podstawy ostrosłupa trójkątnego prawidłowego jest równa 6. Jego objętość jest równa 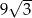 . Wyznacz długość wysokości ściany bocznej ostrosłupa.
. Wyznacz długość wysokości ściany bocznej ostrosłupa.
Krawędź boczna ostrosłupa prawidłowego trójkątnego jest dwa razy dłuższa od krawędzi podstawy. Krawędź podstawy jest równa  . Oblicz pole powierzchni bocznej i sinus połowy kąta między ścianami bocznymi ostrosłupa.
. Oblicz pole powierzchni bocznej i sinus połowy kąta między ścianami bocznymi ostrosłupa.
Podstawą ostrosłupa 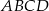 jest trójkąt równoboczny
jest trójkąt równoboczny 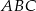 o boku długości
o boku długości 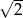 . Wszystkie ściany boczne są równoramiennymi trójkątami prostokątnymi. Punkt
. Wszystkie ściany boczne są równoramiennymi trójkątami prostokątnymi. Punkt 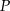 został wybrany wewnątrz ostrosłupa w ten sposób, że wysokości ostrosłupów
został wybrany wewnątrz ostrosłupa w ten sposób, że wysokości ostrosłupów 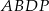 ,
, 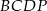 ,
, 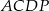 ,
, 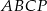 opuszczone z wierzchołka
opuszczone z wierzchołka 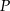 mają tę samą długość
mają tę samą długość 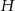 . Sporządź rysunek ostrosłupa i oblicz
. Sporządź rysunek ostrosłupa i oblicz 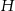 .
.
W ostrosłupie prawidłowym trójkątnym krawędzie boczne są dwa razy dłuższe od krawędzi podstawy.
- Wyznacz sinus kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy.
- Wyznacz długość krawędzi podstawy, tak aby objętość ostrosłupa wynosiła
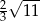 .
.
Podstawą ostrosłupa prawidłowego trójkątnego 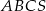 jest trójkąt
jest trójkąt 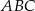 . Punkty
. Punkty 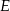 i
i 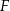 są rzutami punktów
są rzutami punktów 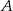 i
i 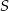 na przeciwległe ściany. Oblicz w jakim stosunku odcinek
na przeciwległe ściany. Oblicz w jakim stosunku odcinek 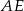 dzieli odcinek
dzieli odcinek 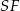 , jeżeli ściana boczna ostrosłupa jest nachylona do podstawy pod kątem, którego sinus jest równy
, jeżeli ściana boczna ostrosłupa jest nachylona do podstawy pod kątem, którego sinus jest równy  .
.

