Kolejne liczby/Podzielność - zadania z matematyki

/Szkoła średnia/Liczby/Liczby całkowite/Podzielność/Kolejne liczby

Wykaż, że iloczyn trzech kolejnych liczb podzielnych przez 3 dzieli się przez 81.

Wykaż, że różnica kwadratów dwóch kolejnych liczb parzystych jest liczbą podzielną przez 4.

Ukryj Podobne zadania

Wykaż, że różnica kwadratów dwóch kolejnych liczb nieparzystych jest liczbą podzielną przez 8.

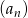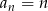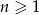Dany ciąg arytmetyczny (an ) taki, że an = n , dla n ≥ 1 . Udowodnij, że iloczyn każdych dziesięciu kolejnych wyrazów tego ciągu jest podzielny przez .

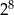Wykaż, że suma kwadratów dwóch kolejnych liczb nieparzystych nie dzieli się przez 4.

Ukryj Podobne zadania

Udowodnij, że suma kwadratów dwóch kolejnych liczb nieparzystych jest liczbą parzystą.

Udowodnij, że różnica sześcianów dwóch kolejnych liczb całkowitych nie jest liczbą podzielną przez 5.

Wykaż, że suma pięciu kolejnych liczb naturalnych nie może być liczbą pierwszą.

Wykaż, że suma sześcianów trzech kolejnych liczb naturalnych parzystych jest podzielna przez 24.

Ukryj Podobne zadania

Wykaż, że suma sześcianów trzech kolejnych liczb naturalnych nieparzystych jest podzielna przez 3.

Uzasadnij, że suma trzech kolejnych potęg liczby 2 o wykładnikach całkowitych dodatnich jest podzielna przez 14.

Udowodnij, że po wymnożeniu kolejnych liczb naturalnych od 1 do 30, czyli po wykonaniu działania 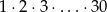1 ⋅2 ⋅3⋅... ⋅30 , otrzymamy liczbę, która kończy się dokładnie 7 zerami.

Udowodnij, że iloczyn kolejnych liczb naturalnych od 1 do 16, czyli 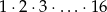1 ⋅2 ⋅3⋅... ⋅16 , jest podzielny przez 215 .

Ukryj Podobne zadania

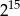Udowodnij, że iloczyn kolejnych liczb naturalnych od 1 do 21, czyli 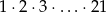1 ⋅2 ⋅3⋅... ⋅21 , jest podzielny przez .

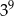Uzasadnij, że suma kwadratów trzech kolejnych liczb parzystych nigdy nie jest liczbą podzielną przez 3.

Ukryj Podobne zadania

Uzasadnij, że suma kwadratów trzech kolejnych liczb nieparzystych nigdy nie jest liczbą podzielną przez 3.

Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.

Ukryj Podobne zadania

Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych nieparzystych jest podzielna przez 9.

Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych niepodzielnych przez 4 jest liczbą podzielną przez 36.