Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość 4 cm, a wysokość jego ściany bocznej ma długość 5 cm. Pole powierzchni bocznej tego ostrosłupa jest równe
A) 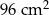 B)
B) 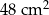 C)
C) 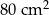 D)
D) 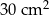
/Szkoła podstawowa/Zadania testowe/Figury przestrzenne/Ostrosłup
Dany jest ostrosłup prawidłowy czworokątny. Pole powierzchni całkowitej tej bryły jest równe 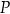 , a jedna ściana boczna ma pole równe
, a jedna ściana boczna ma pole równe 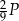 . Pole powierzchni bocznej tego ostrosłupa jest równe A/B.
. Pole powierzchni bocznej tego ostrosłupa jest równe A/B.
A) 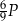 B)
B) 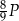
Pole powierzchni podstawy tego ostrosłupa jest dwa razy C/D niż pole powierzchni jego jednej ściany bocznej.
C) mniejsze D) większe
Na rysunku przedstawiono prostokąt i dwa trójkąty równoramienne 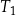 i
i 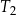 oraz podano długości ich boków.
oraz podano długości ich boków.
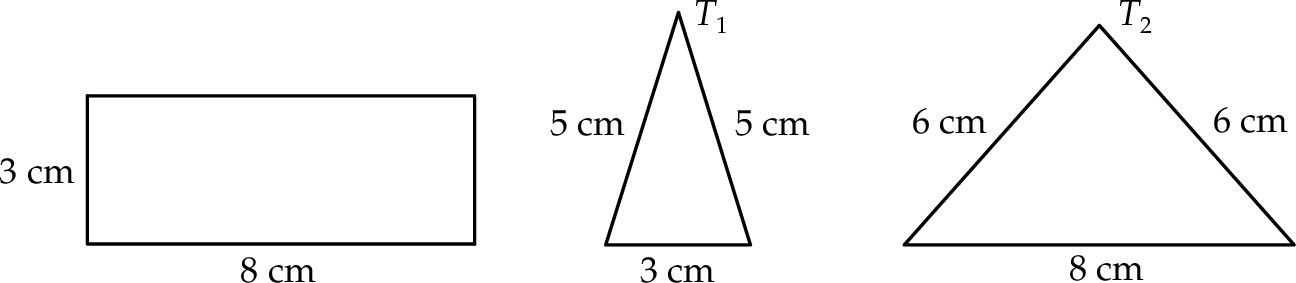
Czy te trzy wielokąty mogą być ścianami jednego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | długości boków prostokąta są równe długościom podstaw trójkątów 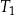 i i 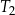 . . |
| B) | trójkąty 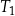 i i 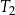 mają podstawy różnej długości. mają podstawy różnej długości. |
| C) | ramiona trójkąta 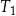 mają inną długość niż ramiona trójkąta mają inną długość niż ramiona trójkąta 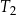 . . |
Na rysunku przedstawiono prostokąt i dwa trójkąty równoramienne 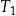 i
i 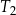 oraz podano długości ich boków.
oraz podano długości ich boków.
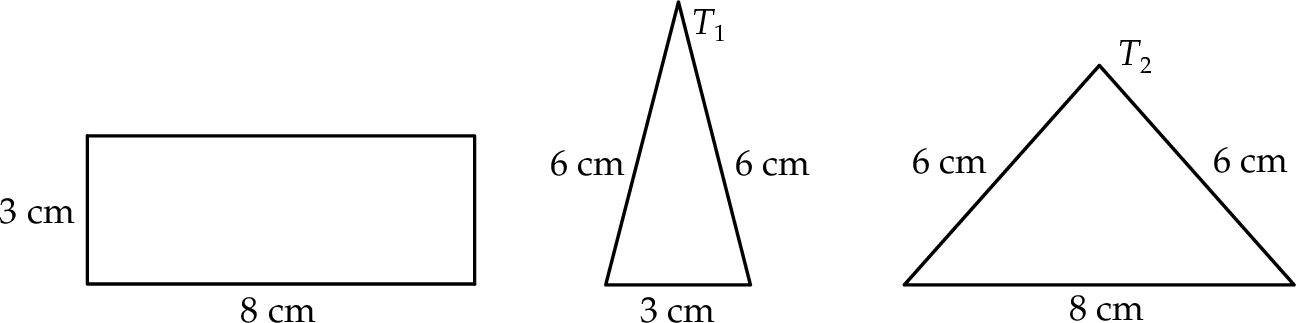
Czy te trzy wielokąty mogą być ścianami jednego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | długości boków prostokąta są równe długościom podstaw trójkątów 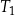 i i 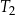 . . |
| B) | trójkąty 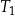 i i 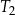 mają podstawy różnej długości. mają podstawy różnej długości. |
| C) | ramiona trójkątów 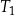 i i 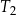 nie są równe długościom boków prostokąta. nie są równe długościom boków prostokąta. |
Siatka ostrosłupa składa się z kwadratu i czterech trójkątów prostokątnych zbudowanych na bokach tego kwadratu.
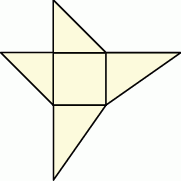
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wysokość tego ostrosłupa jest równa długości jednej z jego krawędzi. | P | F |
| Wszystkie wysokości ścian bocznych tego ostrosłupa mają taką samą długość. | P | F |
Liczba ścian ostrosłupa prawidłowego jest o 5 mniejsza niż liczba jego krawędzi. Pole powierzchni całkowitej tego ostrosłupa jest równe 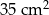 , a pole podstawy jest równe
, a pole podstawy jest równe 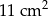 . Pole jednej ściany bocznej tego ostrosłupa jest równe
. Pole jednej ściany bocznej tego ostrosłupa jest równe
A) 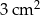 B)
B) 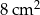 C)
C) 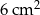 D)
D) 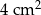
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego czworokątnego.
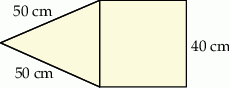
Suma długości wszystkich krawędzi tego ostrosłupa jest równa
A) 560 cm B) 360 cm C) 260 cm D) 220 cm
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego trójkątnego.
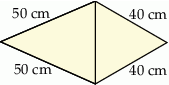
Suma długości wszystkich krawędzi tego ostrosłupa jest równa
A) 560 cm B) 360 cm C) 260 cm D) 270 cm
Suma długości wszystkich krawędzi ostrosłupa prawidłowego sześciokątnego jest równa 450. Krawędź boczna jest w tym ostrosłupie czterokrotnie dłuższa od krawędzi podstawy.
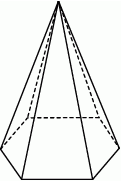
Długość krawędzi podstawy tego ostrosłupa jest równa
A) 15 B) 25 C) 50 D) 60
Suma długości wszystkich krawędzi ostrosłupa prawidłowego sześciokątnego jest równa 540. Krawędź boczna jest w tym ostrosłupie pięciokrotnie dłuższa od krawędzi podstawy.
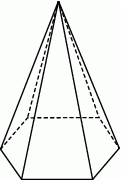
Długość krawędzi podstawy tego ostrosłupa jest równa
A) 15 B) 25 C) 50 D) 60
Rysunek przedstawia ostrosłup prosty.
Oceń, czy podane zdania są prawdziwe. Zaznacz P (prawda) lub F (fałsz).
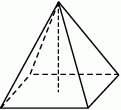
| Ściany boczne ostrosłupa są trójkątami prostokątnymi. | P | F |
| Liczba wszystkich krawędzi ostrosłupa jest parzysta. | P | F |
| Wszystkie ściany boczne ostrosłupa mają wspólny wierzchołek. | P | F |
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego czworokątnego.
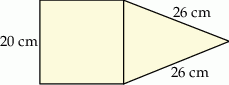
Suma długości krawędzi bocznych tego ostrosłupa jest równa A/B.
A) 360 cm B) 104 cm
Pole powierzchni całkowitej tego ostrosłupa jest równa C/D.
C) 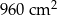 D)
D) 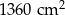
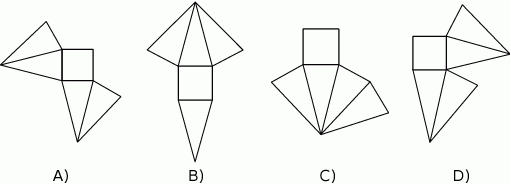
Który z poniższych rysunków nie może być siatką ostrosłupa prawidłowego czworokątnego?
Z jednakowych czworościennych klocków ułożono bryłę mającą kształt czworościanu foremnego.
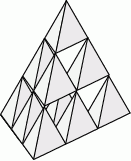
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Utworzona bryła składa się z 10 klocków. | P | F |
| Czworościan foremny o wymiarach takich jak utworzona figura ma objętość 27 razy większą od objętości jednego klocka. | P | F |
Maciek rysuje siatkę ostrosłupa prawidłowego, którego podstawą jest kwadrat o środku w punkcie 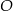 i boku długości 8.
i boku długości 8.
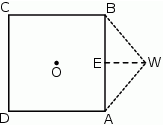
Czy trójkąt 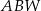 o bokach długości odpowiednio: 8, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
o bokach długości odpowiednio: 8, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | trójkąt 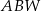 jest równoramienny. jest równoramienny. |
| B) | odległość 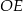 jest mniejsza niż wysokość jest mniejsza niż wysokość 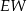 trójkąta trójkąta 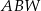 . . |
| C) | odległość 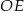 jest większa niż wysokość jest większa niż wysokość 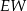 trójkąta trójkąta 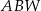 . . |
Hela rysuje siatkę ostrosłupa, którego podstawą jest prostokątny trójkąt równoramienny 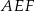 .
.
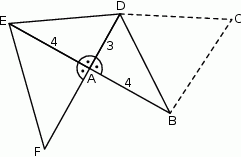
Czy trójkąt równoboczny 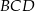 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | odcinki 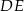 i i 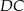 mają różne długości. mają różne długości. |
| B) | odcinki 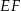 i i 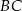 mają różne długości. mają różne długości. |
| C) | odcinki 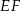 i i 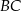 mają równe długości. mają równe długości. |
Maciek rysuje siatkę ostrosłupa prawidłowego, którego podstawą jest kwadrat o środku w punkcie 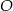 i boku długości 6.
i boku długości 6.
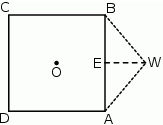
Czy trójkąt 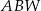 o bokach długości odpowiednio: 6, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
o bokach długości odpowiednio: 6, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | trójkąt 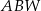 jest równoramienny. jest równoramienny. |
| B) | odległość 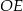 jest mniejsza niż wysokość jest mniejsza niż wysokość 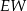 trójkąta trójkąta 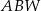 . . |
| C) | odległość 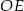 jest większa niż wysokość jest większa niż wysokość 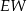 trójkąta trójkąta 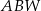 . . |
Staś ma dwa jednakowe klocki w kształcie ostrosłupa prawidłowego czworokątnego, każdy o polu powierzchni całkowitej 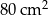 . Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
. Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
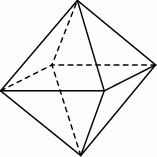
Jakie pole powierzchni ma bryła otrzymana przez Stasia?
A) 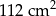 B)
B) 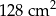 C)
C) 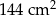 D)
D) 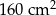
Kacper ma dwa jednakowe klocki w kształcie ostrosłupa prawidłowego sześciokątnego, każdy o polu powierzchni całkowitej 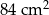 . Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
. Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
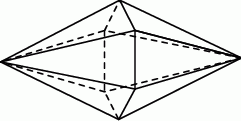
Jakie pole powierzchni ma bryła otrzymana przez Stasia?
A) 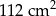 B)
B)  C)
C) 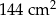 D)
D) 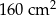
Rysunki przedstawiają bryłę, której wszystkie cztery ściany są trójkątami równobocznymi.

Które wielokąty – I, II, III – przedstawiają siatki bryły takiej, jaką pokazano na powyższych rysunkach?
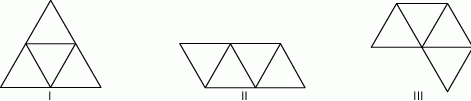
A) I, II i III B) tylko I i III C) tylko II i III D) tylko I i II
Rysunki przedstawiają bryłę, której wszystkie cztery ściany są trójkątami równobocznymi.

Które wielokąty – I, II, III – przedstawiają siatki bryły takiej, jaką pokazano na powyższych rysunkach?
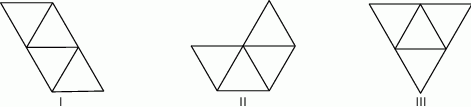
A) I, II i III B) tylko I i III C) tylko II i III D) tylko I i II
Wysokość ściany bocznej opuszczona na krawędź podstawy ostrosłupa prawidłowego trójkątnego jest 3 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej do pola powierzchni podstawy tego ostrosłupa jest równy
A) 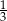 B)
B) 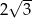 C)
C) 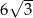 D) 9
D) 9
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli długość każdej krawędzi podstawy ostrosłupa prawidłowego czworokątnego zwiększymy 2 razy, a jego wysokość zmniejszymy 2 razy, to objętość ostrosłupa
A) zwiększy się czterokrotnie. B) zwiększy się dwukrotnie.
C) zmniejszy się dwukrotnie. D) nie zmieni się.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli długość każdej krawędzi podstawy ostrosłupa prawidłowego czworokątnego zmniejszymy 2 razy, a jego wysokość zwiększymy 4 razy, to objętość ostrosłupa
A) zwiększy się czterokrotnie. B) zwiększy się dwukrotnie.
C) zmniejszy się dwukrotnie. D) nie zmieni się.
Siatka ostrosłupa składa się z kwadratu i trójkątów równobocznych zbudowanych na bokach tego kwadratu.
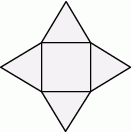
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wszystkie krawędzie tego ostrosłupa mają taką samą długość. | P | F |
| Wysokość tego ostrosłupa jest mniejsza niż wysokość jego ściany bocznej. | P | F |
Siatka ostrosłupa składa się z czterech trójkątów równobocznych.
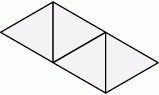
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Ostrosłup ten ma 6 krawędzi. | P | F |
| Wysokość tego ostrosłupa jest równa długości jego krawędzi. | P | F |
Obwód podstawy ostrosłupa prawidłowego siedmiokątnego jest równy 33,6 cm, a długość jego krawędzi bocznej jest równa 2,5 cm. Pole powierzchni bocznej tego ostrosłupa jest równe
A) 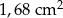 B)
B) 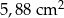 C)
C) 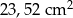 D)
D) 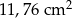
Ostrosłupy prawidłowe trójkątne 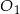 i
i 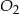 mają takie same wysokości. Długość krawędzi podstawy ostrosłupa
mają takie same wysokości. Długość krawędzi podstawy ostrosłupa 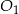 jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa
jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa 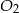 . Stosunek objętości ostrosłupa
. Stosunek objętości ostrosłupa 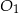 do objętości ostrosłupa
do objętości ostrosłupa 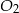 jest równy
jest równy
A) 3 : 1 B) 1 : 3 C) 9 : 1 D) 1 : 9
Rysunek przedstawia siatkę ostrosłupa prostego o podstawie będącej prostokątem.
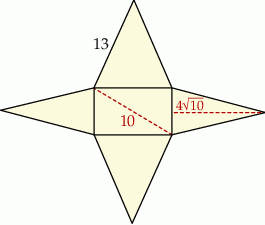
Objętość tego ostrosłupa jest równa
A) 192 B) 96 C) 576 D) 384

