Na rysunku poniżej przedstawiono fragment wykresu funkcji 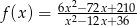 określonej dla
określonej dla 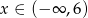 . Wykres ten przecina osie
. Wykres ten przecina osie 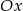 i
i 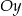 odpowiednio w punktach
odpowiednio w punktach 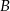 i
i 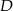 , a punkt
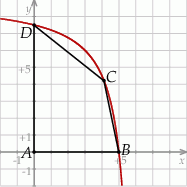
, a punkt 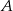 jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty
jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty 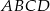 , w których punkt
, w których punkt 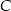 leży na wykresie funkcji
leży na wykresie funkcji 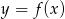 pomiędzy punktami
pomiędzy punktami 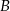 i
i 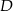 .
.
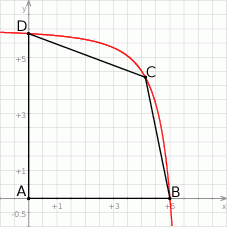
Oblicz pierwszą współrzędną wierzchołka 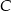 tego z rozpatrywanych czworokątów, którego pole jest największe.
tego z rozpatrywanych czworokątów, którego pole jest największe.

 , a pozostałe dwa należą do paraboli o równaniu
, a pozostałe dwa należą do paraboli o równaniu 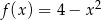 i znajdują się powyżej osi
i znajdują się powyżej osi  .
. 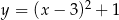 . Tworzymy trójkąty
. Tworzymy trójkąty 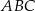 takie, że punkt
takie, że punkt 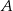 leży w początku układu współrzędnych, punkt
leży w początku układu współrzędnych, punkt 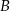 o współrzędnych
o współrzędnych 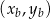 leży na paraboli, punkt
leży na paraboli, punkt 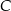 ma współrzędne
ma współrzędne 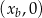 .
. 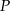 , określającej pole trójkąta
, określającej pole trójkąta 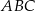 w zależności od
w zależności od 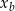 dla
dla 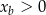 .
. ![xb ∈ [0;2]](https://img.zadania.info/zad/3724416/HzadT11x.gif) ; w odpowiedzi podaj współrzędne punktu
; w odpowiedzi podaj współrzędne punktu 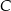 .
.![[− 1,7]](https://img.zadania.info/zad/5154135/HzadT0x.gif) określono dwie funkcje:
określono dwie funkcje: 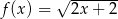 i
i 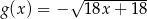 . Rozpatrujemy wszystkie trapezy
. Rozpatrujemy wszystkie trapezy 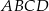 , których wierzchołki
, których wierzchołki 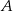 i
i 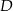 leżą na wykresie funkcji
leżą na wykresie funkcji 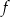 , a wierzchołki
, a wierzchołki 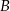 i
i 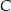 leżą na wykresie funkcji
leżą na wykresie funkcji 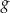 . Podstawy rozpatrywanych trapezów są równoległe do osi
. Podstawy rozpatrywanych trapezów są równoległe do osi 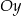 (zobacz rysunek).
(zobacz rysunek). 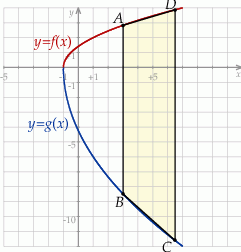
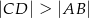 , i który ma największe możliwe pole. Oblicz to największe pole. Przy rozwiązywaniu zadania możesz skorzystać z tego, że jeżeli pierwsza współrzędna wierzchołka
, i który ma największe możliwe pole. Oblicz to największe pole. Przy rozwiązywaniu zadania możesz skorzystać z tego, że jeżeli pierwsza współrzędna wierzchołka 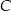 trapezu
trapezu 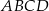 jest równa 7, a druga współrzędna wierzchołka
jest równa 7, a druga współrzędna wierzchołka 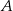 jest równa
jest równa 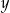 , to pole trapezu wyraża się wzorem
, to pole trapezu wyraża się wzorem 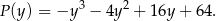
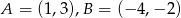 . Wyznacz taki punkt
. Wyznacz taki punkt 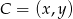 , gdzie
, gdzie 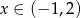 leżący na paraboli o równaniu
leżący na paraboli o równaniu 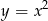 , aby pole trójkąta
, aby pole trójkąta 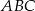 było największe.
było największe. 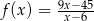 określonej dla
określonej dla 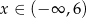 . Wykres ten przecina osie
. Wykres ten przecina osie 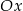 i
i 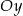 odpowiednio w punktach
odpowiednio w punktach 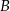 i
i 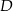 , a punkt
, a punkt 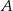 jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty
jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty 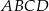 , w których punkt
, w których punkt 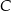 leży na wykresie funkcji
leży na wykresie funkcji 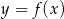 pomiędzy punktami
pomiędzy punktami 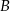 i
i  .
. 
 tego z rozpatrywanych czworokątów, którego pole jest największe.
tego z rozpatrywanych czworokątów, którego pole jest największe. 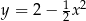 przecina oś
przecina oś 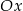 układu współrzędnych w punktach
układu współrzędnych w punktach 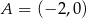 i
i 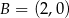 . Rozpatrujemy wszystkie trapezy równoramienne
. Rozpatrujemy wszystkie trapezy równoramienne 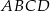 , których dłuższą podstawą jest odcinek
, których dłuższą podstawą jest odcinek 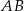 , a końce
, a końce 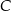 i
i 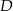 krótszej podstawy leżą na paraboli (zobacz rysunek).
krótszej podstawy leżą na paraboli (zobacz rysunek). 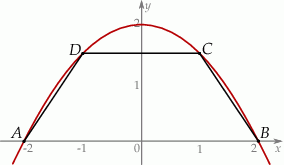
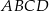 w zależności od pierwszej współrzędnej wierzchołka
w zależności od pierwszej współrzędnej wierzchołka 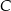 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 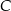 tego z rozpatrywanych trapezów, którego pole jest największe.
tego z rozpatrywanych trapezów, którego pole jest największe. 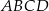 , których dwa wierzchołki
, których dwa wierzchołki 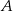 i
i 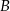 leżą na odcinku o końcach
leżą na odcinku o końcach 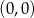 i
i 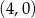 , a dwa pozostałe wierzchołki
, a dwa pozostałe wierzchołki 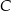 i
i 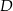 leżą na paraboli o równaniu
leżą na paraboli o równaniu 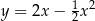 (zobacz rysunek).
(zobacz rysunek). 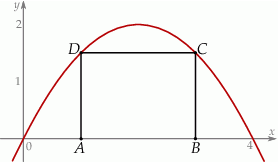
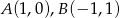 . Punkt
. Punkt 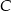 należy do okręgu o równaniu
należy do okręgu o równaniu 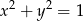 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 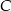 tak, aby pole trójkąta
tak, aby pole trójkąta 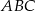 było największe. Oblicz to pole.
było największe. Oblicz to pole. 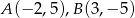 . Punkt
. Punkt 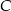 należy do okręgu o równaniu
należy do okręgu o równaniu 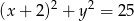 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 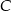 tak, aby pole trójkąta
tak, aby pole trójkąta 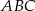 było największe. Oblicz to pole.
było największe. Oblicz to pole. 