Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny

Wyszukiwanie zadań

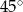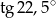Korzystając z własności trójkąta prostokątnego o kącie ostrym ∘ 45 oblicz tg 22,5∘ .

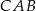Kąt CAB trójkąta prostokątnego 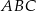ABC ma miarę 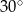∘ 30 . Odcinek 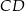CD jest wysokością tego trójkąta opuszczoną na przeciwprostokątną 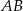AB . Oblicz stosunek pól trójkątów 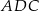ADC i CDB .

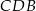Z wierzchołka kąta prostego trójkąta prostokątnego 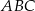ABC poprowadzono wysokość 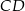CD , która podzieliła przeciwprostokątną 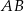AB na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).

PIC

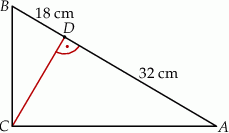
Oblicz pole trójkąta ABC .

Trójkąt prostokątny ABC ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych.

Na podstawie twierdzenia Pitagorasa można udowodnić bardziej ogólną własność niż ta, o której mówi samo to twierdzenie.

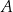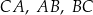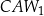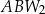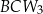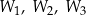Rozważmy trójkąt prostokątny ABC o kącie prostym przy wierzchołku A . Niech każdy z boków tego trójkąta: CA , AB , BC będzie podstawą trójkątów podobnych, odpowiednio: CAW 1 , ABW 2 , BCW 3 . Trójkąty te mają odpowiadające sobie kąty o równych miarach, odpowiednio przy wierzchołkach: W 1, W 2, W 3 .

ZINFO-FIGURE

Pola trójkątów: 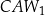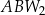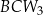CAW 1 , ABW 2 , BCW 3 oznaczymy odpowiednio jako 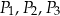P 1,P 2,P3 . Udowodnij, że

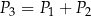
P = P + P 3 1 2

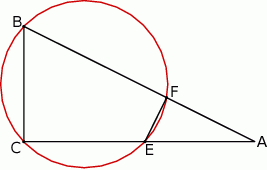
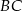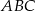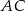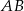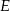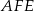Okrąg przechodzący przez końce przyprostokątnej BC trójkąta prostokątnego ABC przecina drugą przyprostokątną AC oraz przeciwprostokątną AB tego trójkąta odpowiednio w punktach E i F . Wykaż, że promień okręgu opisanego na trójkącie AF E jest równy 1|AE | 2 .

PIC

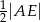Oblicz sumę długości boków i pole trójkąta prostokątnego, w którym jedna z przyprostokątnych jest równa 10 cm, a druga jest o 2 cm krótsza od przeciwprostokątnej.

Promień okręgu opisanego na trójkącie prostokątnym ma długość 3 dm, a długość promienia okręgu wpisanego w trójkąt prostokątny wynosi 1 dm. Oblicz obwód tego trójkąta.

Oblicz sumę tangensów kątów ostrych trójkąta prostokątnego wiedząc że stosunek pola tego trójkąta do pola kwadratu, którego bokiem jest przeciwprostokątna danego trójkąta wynosi 16 .

Ukryj Podobne zadania

Stosunek pola trójkąta prostokątnego do pola kwadratu, zbudowanego na przeciwprostokątnej tego trójkąta jest równy 18 . Oblicz sumę tangensów kątów ostrych tego trójkąta.

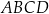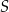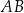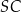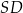Przekątne trapezu ABCD są prostopadłe i przecinają się w punkcie S . Podstawa AB tego trapezu ma długość 15, a odcinki SC i SD mają odpowiednio długości 6 i 8. Oblicz pole trójkąta ABS .

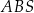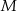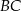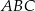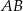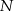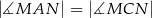Punkt M przyprostokątnej BC trójkąta prostokątnego ABC zrzutowano na przeciwprostokątną AB otrzymując punkt N . Wykaż, że |∡MAN | = |∡MCN | .

Miara jednego z kątów ostrych w trójkącie prostokątnym jest równa α .

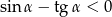  • Uzasadnij, że spełniona jest nierówność sin α− tg α < 0 .
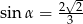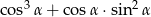  • Dla √ - sin α = 2--2 3 oblicz wartość wyrażenia cos3α + co sα ⋅sin 2α .

W trójkącie prostokątnym jedna z przyprostokątnych jest średnią arytmetyczną drugiej przyprostokątnej i przeciwprostokątnej. Oblicz sinusy kątów ostrych tego trójkąta.

Ukryj Podobne zadania

W trójkącie prostokątnym stosunek sumy długości przyprostokątnych do długości przeciwprostokątnej jest równy 54 . Oblicz cosinusy kątów ostrych tego trójkąta.

W trójkącie prostokątnym stosunek różnicy długości przyprostokątnych do długości przeciwprostokątnej jest równy 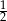12 . Oblicz cosinusy kątów ostrych tego trójkąta.

Przeciwprostokątna trójkąta prostokątnego ma długość 26 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.

Ukryj Podobne zadania

Przeciwprostokątna trójkąta prostokątnego ma długość 34 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.

Na okręgu o promieniu 2 opisano trójkąt prostokątny o jednej z przyprostokątnych długości 12. Oblicz obwód tego trójkąta.

Ukryj Podobne zadania

Na okręgu o promieniu 3 opisano trójkąt prostokątny o jednej z przyprostokątnych długości 12. Oblicz obwód tego trójkąta.

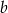Długości a i b przyprostokątnych trójkąta prostokątnego spełniają równość

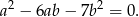
a 2 − 6ab − 7b 2 = 0.
  • Oblicz tangensy kątów ostrych tego trójkąta.
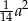  • Uzasadnij, że pole tego trójkąta jest równe -1a2 14 .

Korzystając z danych przedstawionych na rysunku oblicz wartość wyrażenia

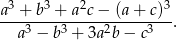
3 3 2 3 a-+--b-+--a-c−--(a+-c)--. a3 − b3 + 3a2b − c3

PIC

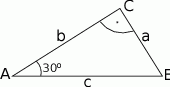
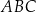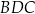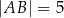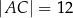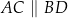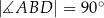Trójkąty prostokątne ABC i BDC spełniają warunki: |AB | = 5 , |AC | = 12 , AC ∥ BD oraz |∡ABD | = 90∘ (zobacz rysunek).

ZINFO-FIGURE

Oblicz długość odcinka 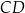CD .

W trójkącie prostokątnym suma cosinusów kątów ostrych jest równa 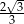2√-3 3 . Wykaż, że iloczyn sinusów tych kątów jest równy 16 .

Ukryj Podobne zadania

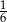W trójkącie prostokątnym suma sinusów kątów ostrych jest równa 3 2 . Wykaż, że iloczyn cosinusów tych kątów jest równy 58 .

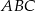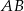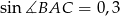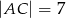Dany jest trójkąt prostokątny ABC o przeciwprostokątnej AB , taki że sin ∡BAC = 0,3 i |AC | = 7 . Oblicz pole koła opisanego na tym trójkącie.

Strona 2 z 7