W pewnym trójkącie prostokątnym suma cosinusów kątów ostrych jest równa 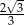 . Oblicz iloczyn sinusów tych kątów.
. Oblicz iloczyn sinusów tych kątów.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny
Suma sinusów kątów ostrych w pewnym trójkącie prostokątnym wynosi 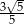 . Oblicz iloczyn sinusów tych kątów.
. Oblicz iloczyn sinusów tych kątów.
Wyznacz wartości funkcji trygonometrycznych kątów ostrych trójkąta powstałego wskutek połączenia odcinkiem wierzchołka kwadratu ze środkiem przeciwległego boku.
W trójkącie prostokątnym 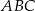 przyprostokątne mają długości:
przyprostokątne mają długości: 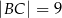 ,
, 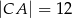 . Na boku
. Na boku 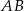 wybrano punkt
wybrano punkt 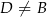 tak, że odcinki
tak, że odcinki 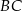 i
i 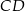 mają równe długości. Oblicz długość odcinka
mają równe długości. Oblicz długość odcinka 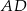 .
.
Wykaż, że w trójkącie prostokątnym suma długości obu przyprostokątnych jest równa sumie długości średnic okręgów wpisanego i opisanego na tym trójkącie.
Przyprostokątne trójkąta prostokątnego mają długości  i
i 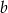 , a jego przeciwprostokątna ma długość
, a jego przeciwprostokątna ma długość  . Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość
. Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość 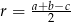 .
.
W trójkącie prostokątnym jedna przyprostokątna jest 4 razy dłuższa od drugiej. Wykaż, że wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest 16 razy dłuższy od drugiego.
W trójkącie prostokątnym jedna przyprostokątna jest 3 razy dłuższa od drugiej. Wykaż, że wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest 9 razy dłuższy od drugiego.
Dwusieczna kąta prostego w trójkącie prostokątnym dzieli przeciwprostokątna w stosunku 3:4. Oblicz stosunek pola koła opisanego na tym trójkącie do pola koła wpisanego w ten trójkąt.
Dany jest trójkąt prostokątny równoramienny 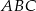 . Punkty
. Punkty 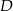 i
i 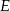 dzielą przeciwprostokątną
dzielą przeciwprostokątną 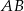 na trzy odcinki równej długości. Oblicz cosinus kąta
na trzy odcinki równej długości. Oblicz cosinus kąta 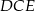 .
.
Pole prostokąta 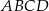 jest równe 60, a promień okręgu wpisanego w trójkąt
jest równe 60, a promień okręgu wpisanego w trójkąt 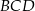 jest równy 2. Oblicz obwód tego prostokąta.
jest równy 2. Oblicz obwód tego prostokąta.
Środek okręgu opisanego na trójkącie prostokątnym leży w odległości 3 cm i 2 cm od przyprostokątnych. Oblicz pole tego trójkąta.
Okrąg wpisany w trójkąt prostokątny 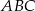 o bokach długości
o bokach długości 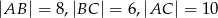 jest styczny do boków
jest styczny do boków 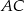 i
i 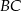 w punktach
w punktach 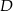 i
i 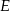 . Proste
. Proste 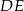 i
i 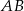 przecinają się punkcie
przecinają się punkcie 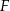 . Oblicz pole trójkąta
. Oblicz pole trójkąta 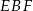 .
.
W trójkącie prostokątnym, w którym przyprostokątne mają długości 2 i 4, jeden z kątów ostrych ma miarę  . Oblicz
. Oblicz 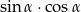 .
.
W trójkącie prostokątnym przyprostokątne mają długości 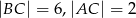 . Wyznacz wartość wyrażenia
. Wyznacz wartość wyrażenia 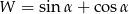 , gdzie
, gdzie  jest najmniejszym kątem ostrym tego trójkąta.
jest najmniejszym kątem ostrym tego trójkąta.
W trójkącie prostokątnym przyprostokątne mają długości 3 i 5, a jeden z kątów ostrych ma miarę  . Oblicz
. Oblicz 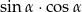 .
.
W trójkącie prostokątnym przyprostokątne mają długości 2 i 4, a jeden z kątów ostrych ma miarę  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 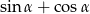 .
.
W trójkącie prostokątnym przyprostokątne mają długości 1 i 3, a jeden z kątów ostrych ma miarę  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 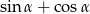 .
.
W trójkącie prostokątnym 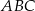 (
(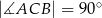 ,
, 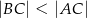 ) poprowadzono prostą przechodzącą przez wierzchołek
) poprowadzono prostą przechodzącą przez wierzchołek 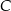 trójkąta która przecina przeciwprostokątną w punkcie
trójkąta która przecina przeciwprostokątną w punkcie 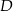 , takim, że
, takim, że 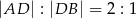 . Oblicz długość przeciwprostokątnej jeśli
. Oblicz długość przeciwprostokątnej jeśli 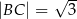 i
i 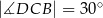 .
.
Wyznacz długości boków oraz miary kątów trójkąta prostokątnego jeżeli 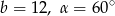 .
.
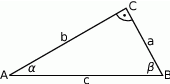
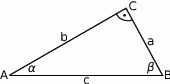
Wyznacz długości boków oraz miary kątów trójkąta prostokątnego jeżeli 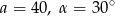 .
.
Wykaż, że jeśli 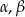 są kątami ostrymi trójkąta prostokątnego, to
są kątami ostrymi trójkąta prostokątnego, to 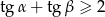 .
.
W trójkącie prostokątnym 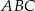 przyprostokątne mają długości
przyprostokątne mają długości 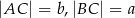 , a wysokość opuszczona z wierzchołka kąta prostego ma długość
, a wysokość opuszczona z wierzchołka kąta prostego ma długość 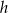 .
.
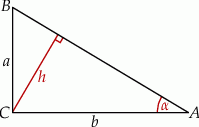
Wykaż, że jeżeli 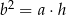 to
to 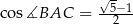 .
.
Stosunek długości przyprostokątnych trójkąta prostokątnego wynosi 3:8, a środkowa poprowadzona do dłuższej przyprostokątnej ma długość 15.
- Oblicz długość przyprostokątnych trójkąta.
- Oblicz odległość środka ciężkości trójkąta od dłuższej przyprostokątnej.
Jeden kąt ostry trójkąta prostokątnego ma miarę  . Wyznacz długości boków tego trójkąta wiedząc, że wysokość poprowadzona z wierzchołka kąta prostego ma długość
. Wyznacz długości boków tego trójkąta wiedząc, że wysokość poprowadzona z wierzchołka kąta prostego ma długość 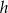 .
.
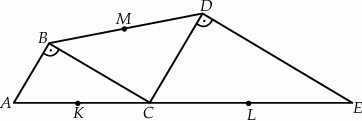
Trójkąty 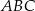 i
i 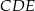 są prostokątne oraz
są prostokątne oraz 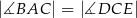 . Punkty
. Punkty 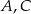 i
i 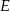 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 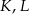 i
i 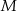 są środkami odcinków
są środkami odcinków 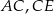 i
i 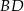 (zobacz rysunek). Wykaż, że kąt
(zobacz rysunek). Wykaż, że kąt 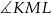 jest prosty.
jest prosty.
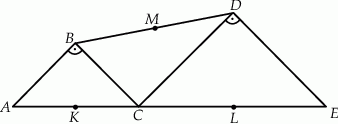
Trójkąty 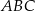 i
i 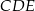 są równoramienne i prostokątne. Punkty
są równoramienne i prostokątne. Punkty 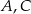 i
i 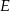 leżą na jednej prostej, a punkty
leżą na jednej prostej, a punkty 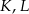 i
i 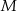 są środkami odcinków
są środkami odcinków 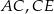 i
i 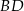 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 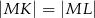 .
.
Dany jest trójkąt prostokątny. Wykaż, że suma pól kół o średnicach będących przyprostokątnymi trójkąta jest równa polu koła o średnicy równej przeciwprostokątnej.
Na bokach trójkąta prostokątnego zbudowano trójkąty równoboczne. Wykaż, że pole figury zbudowanej na przeciwprostokątnej jest równe sumie pól figur zbudowanych na przyprostokątnych.
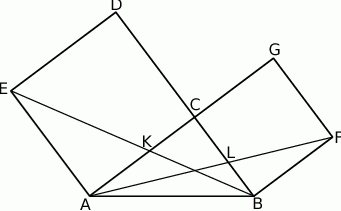
Na przyprostokątnych 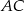 i
i 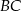 trójkąta prostokątnego
trójkąta prostokątnego 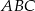 zbudowano, na zewnątrz trójkąta, kwadraty
zbudowano, na zewnątrz trójkąta, kwadraty 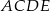 i
i 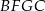 . Odcinek
. Odcinek 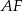 przecina przyprostokątną
przecina przyprostokątną 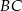 w punkcie
w punkcie 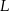 , a odcinek
, a odcinek 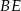 przecina przyprostokątną
przecina przyprostokątną 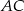 w punkcie
w punkcie 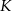 (zobacz rysunek). Udowodnij, że
(zobacz rysunek). Udowodnij, że 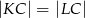 .
.