W trójkącie prostokątnym  jedna z przyprostokątnych jest o 7 dłuższa od drugiej, a promień okręgu wpisanego w ten trójkąt jest równy 3. Oblicz obwód trójkąta
jedna z przyprostokątnych jest o 7 dłuższa od drugiej, a promień okręgu wpisanego w ten trójkąt jest równy 3. Oblicz obwód trójkąta  .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny
W trójkącie prostokątnym iloczyn sinusa jednego z kątów ostrych i tangensa drugiego kąta ostrego jest równy 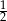 . Oblicz miary kątów ostrych tego trójkąta.
. Oblicz miary kątów ostrych tego trójkąta.
Na przyprostokątnych 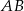 i
i 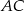 trójkąta prostokątnego równoramiennego
trójkąta prostokątnego równoramiennego 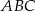 zaznaczono odpowiednio punkty
zaznaczono odpowiednio punkty 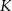 i
i 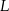 tak, że
tak, że 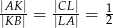 . Odcinki
. Odcinki 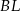 i
i 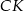 przecinają się w punkcie
przecinają się w punkcie 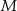 . Oblicz
. Oblicz 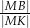 .
.
Wysokość poprowadzona z wierzchołka kąta prostego trójkąta prostokątnego dzieli przeciwprostokątna na odcinki o długościach 1 i 2. Oblicz długości boków tego trójkąta.
W trójkącie prostokątnym 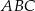 przyprostokątne mają długości:
przyprostokątne mają długości: 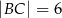 ,
, 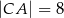 . Na boku
. Na boku 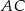 wybrano punkt
wybrano punkt 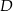 tak, że odcinki
tak, że odcinki 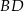 i
i 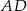 mają równe długości. Oblicz długość odcinka
mają równe długości. Oblicz długość odcinka 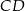 .
.
Dany jest trójkąt o przyprostokątnych 12 i 5. Wyznacz promień okręgu wpisanego w ten trójkąt.
Dany jest trójkąt o przyprostokątnych 24 i 7. Wyznacz promień okręgu wpisanego w ten trójkąt.
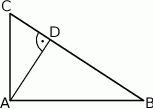
Trójkąt 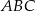 jest prostokątny. Punkt
jest prostokątny. Punkt 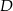 jest spodkiem wysokości opuszczonej na przeciwprostokątną
jest spodkiem wysokości opuszczonej na przeciwprostokątną 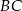 oraz
oraz 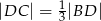 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 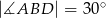 .
.
Trójkąty prostokątne 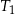 i
i 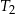 są podobne. Przyprostokątne trójkąta
są podobne. Przyprostokątne trójkąta 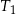 mają długości 5 i 12. Przeciwprostokątna trójkąta
mają długości 5 i 12. Przeciwprostokątna trójkąta 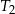 ma długość 26. Oblicz pole trójkąta
ma długość 26. Oblicz pole trójkąta 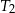 .
.
Trójkąty prostokątne 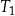 i
i 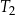 są podobne. Przyprostokątne trójkąta
są podobne. Przyprostokątne trójkąta 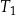 mają długości 7 i 24. Przeciwprostokątna trójkąta
mają długości 7 i 24. Przeciwprostokątna trójkąta 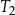 ma długość 50. Oblicz pole trójkąta
ma długość 50. Oblicz pole trójkąta 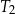 .
.
W trójkącie prostokątnym odległość punktu przecięcia się środkowych od wierzchołka kąta prostego wynosi 2 cm. Wysokość trójkąta poprowadzona na przeciwprostokątną ma długość 2,5 cm. Oblicz pole tego trójkąta.
Dany jest trójkąt prostokątny 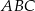 . Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta
. Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta 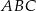 , który ma większą miarę.
, który ma większą miarę.
Dany jest trójkąt prostokątny 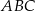 . Przeciwprostokątna tego trójkąta jest 6,5 razy dłuższa niż promień okręgu wpisanego w ten trójkąt. Oblicz sinus tego z kątów ostrych trójkąta
. Przeciwprostokątna tego trójkąta jest 6,5 razy dłuższa niż promień okręgu wpisanego w ten trójkąt. Oblicz sinus tego z kątów ostrych trójkąta 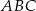 , który ma mniejszą miarę.
, który ma mniejszą miarę.
W trójkącie prostokątnym 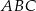 , w którym kąt przy wierzchołku
, w którym kąt przy wierzchołku 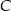 jest kątem prostym, poprowadzono środkowe
jest kątem prostym, poprowadzono środkowe 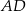 i
i 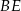 . Udowodnij, że
. Udowodnij, że 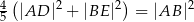 .
.
Liczby 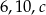 są długościami boków trójkąta prostokątnego. Oblicz
są długościami boków trójkąta prostokątnego. Oblicz  .
.
Punkty 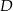 i
i 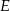 są takimi punktami przeciwprostokątnej
są takimi punktami przeciwprostokątnej 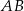 trójkąta prostokątnego
trójkąta prostokątnego 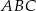 , że
, że 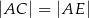 i
i 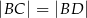 . Wykaż, że
. Wykaż, że 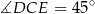 .
.
W trójkącie prostokątnym 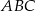 cosinus i tangens kąta przy wierzchołku
cosinus i tangens kąta przy wierzchołku 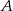 są równe. Oblicz sinus tego kąta.
są równe. Oblicz sinus tego kąta.
Z wierzchołków 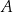 i
i 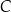 kątów ostrych równoramiennego trójkąta prostokątnego
kątów ostrych równoramiennego trójkąta prostokątnego 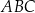 poprowadzono środkowe
poprowadzono środkowe 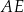 i
i 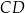 przecinające się w punkcie
przecinające się w punkcie 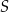 . Oblicz promień okręgu opisanego na trójkącie
. Oblicz promień okręgu opisanego na trójkącie 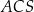 jeżeli
jeżeli 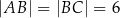 .
.
Dany jest trójkąt prostokątny 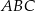 , w którym
, w którym 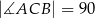 i
i 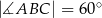 . Niech
. Niech 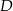 oznacza punkt wspólny wysokości poprowadzonej z wierzchołka
oznacza punkt wspólny wysokości poprowadzonej z wierzchołka 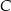 kąta prostego i przeciwprostokątnej
kąta prostego i przeciwprostokątnej 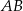 tego trójkąta. Wykaż, że
tego trójkąta. Wykaż, że 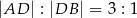 .
.
Na przeciwprostokątnej 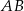 trójkąta prostokątnego
trójkąta prostokątnego 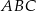 zbudowano kwadrat
zbudowano kwadrat 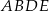 .
.
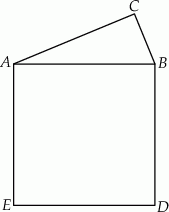
Stosunek pola trójkąta do pola kwadratu jest równy 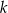 . Wykaż, że suma tangensów kątów ostrych tego trójkąta jest równa
. Wykaż, że suma tangensów kątów ostrych tego trójkąta jest równa 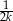 .
.
Sprawdź, czy trójkąt o bokach: 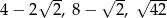 jest trójkątem prostokątnym.
jest trójkątem prostokątnym.
Sprawdź, czy trójkąt o bokach: 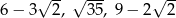 jest trójkątem prostokątnym.
jest trójkątem prostokątnym.
Oblicz wysokość trójkąta prostokątnego o przyprostokątnych 12 cm i 9 cm, która jest poprowadzona do przeciwprostokątnej.
Trójkąt prostokątny ma przyprostokątne długości 12 i 5. Wyznacz długość najkrótszej wysokości tego trójkąta.
Trójkąt prostokątny ma przyprostokątne długości 6 i 8. Wyznacz długość najkrótszej wysokości tego trójkąta.
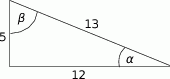
Na rysunku oznaczono kąty oraz podano długości boków trójkąta prostokątnego. Oblicz, które z wyrażeń ma większą wartość: 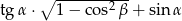 czy
czy 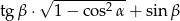 .
.