W trójkącie prostokątnym  wysokość
wysokość 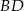 dzieli przeciwprostokątną
dzieli przeciwprostokątną 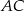 na odcinki o długościach
na odcinki o długościach 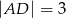 i
i 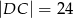 .
.
- Oblicz długości boków trójkąta
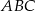 .
. - Oblicz długość odcinka
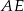 , gdzie
, gdzie 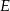 jest punktem wspólnym dwusiecznej kąta
jest punktem wspólnym dwusiecznej kąta 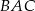 i boku
i boku 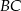 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie prostokątnym 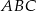 wysokość
wysokość 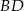 dzieli przeciwprostokątną
dzieli przeciwprostokątną 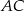 na odcinki o długościach
na odcinki o długościach 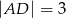 i
i 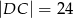 .
.
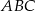 .
. 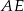 , gdzie
, gdzie 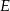 jest punktem wspólnym dwusiecznej kąta
jest punktem wspólnym dwusiecznej kąta 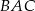 i boku
i boku 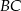 .
.Dany jest trójkąt prostokątny o przyprostokątnych długości: 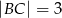 i
i 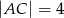 . Na boku
. Na boku 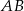 tego trójkąta wybrano taki punkt
tego trójkąta wybrano taki punkt 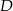 , że
, że 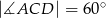 . Oblicz długość odcinka
. Oblicz długość odcinka 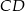 .
.
W trójkącie prostokątnym 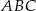 przyprostokątne mają długości
przyprostokątne mają długości 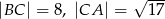 . Na boku
. Na boku 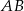 wybrano punkt
wybrano punkt 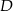 tak, że
tak, że 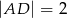 . Oblicz sinus kąta
. Oblicz sinus kąta 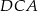 .
.
Przez środek 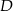 przyprostokątnej
przyprostokątnej 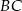 trójkąta prostokątnego
trójkąta prostokątnego 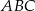 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 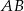 . Prosta ta przecina proste
. Prosta ta przecina proste 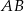 i
i 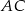 odpowiednio w punktach
odpowiednio w punktach 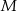 i
i 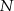 . Wykaż, że
. Wykaż, że 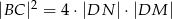 .
.
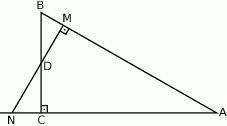
Przez środek 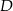 przyprostokątnej
przyprostokątnej 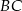 trójkąta prostokątnego
trójkąta prostokątnego 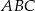 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 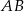 . Prosta ta przecina proste
. Prosta ta przecina proste 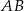 i
i 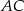 odpowiednio w punktach
odpowiednio w punktach 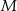 i
i 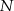 . Wykaż, że skala podobieństwa trójkątów
. Wykaż, że skala podobieństwa trójkątów 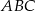 i
i 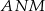 jest równa
jest równa 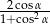 .
.
Wiedząc, że boki trójkąta prostokątnego mają długości: 20, 15, 25, wyznacz długość wysokości opuszczonej na przeciwprostokątną.
Boki trójkąta prostokątnego mają długości 10,24,26. Oblicz długość wysokości opuszczonej na przeciwprostokątną.
Na przyprostokątnych 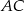 i
i 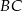 trójkąta prostokątnego
trójkąta prostokątnego 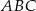 zbudowano trójkąty równoramienne
zbudowano trójkąty równoramienne 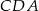 i
i 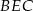 w ten sposób, że
w ten sposób, że 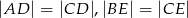 oraz punkty
oraz punkty 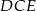 leżą na jednej prostej. Wykaż, że proste
leżą na jednej prostej. Wykaż, że proste 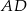 i
i 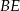 są równoległe.
są równoległe.
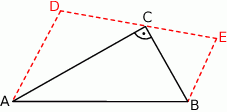
W trójkącie 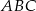 kąt przy wierzchołku
kąt przy wierzchołku 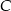 jest prosty. Trójkąt
jest prosty. Trójkąt 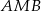 jest równoboczny. Oblicz miary kątów ostrych trójkąta
jest równoboczny. Oblicz miary kątów ostrych trójkąta 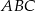 , jeśli pole trójkąta
, jeśli pole trójkąta 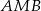 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 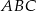 .
.
W trójkącie prostokątnym 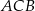 przyprostokątna
przyprostokątna 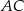 ma długość 5, a promień okręgu wpisanego w ten trójkąt jest równy 2. Oblicz pole trójkąta
ma długość 5, a promień okręgu wpisanego w ten trójkąt jest równy 2. Oblicz pole trójkąta 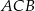 .
.
W trójkącie prostokątnym 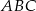 dane są
dane są 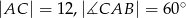 . Poprowadzono prostą równoległą do przeciwprostokątnej
. Poprowadzono prostą równoległą do przeciwprostokątnej 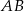 dzielącą bok
dzielącą bok 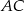 w stosunku
w stosunku 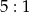 , licząc od wierzchołka
, licząc od wierzchołka 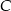 . Prosta ta przecina bok
. Prosta ta przecina bok 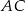 w punkcie
w punkcie 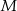 , a bok
, a bok 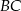 w punkcie
w punkcie 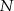 . Oblicz pole trapezu
. Oblicz pole trapezu 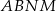 .
.
Uzasadnij, że przeciwprostokątna trójkąta prostokątnego jest średnicą okręgu na nim opisanego.
Oblicz tangens kąta ostrego utworzonego przez proste zawierające środkowe trójkąta prostokątnego równoramiennego poprowadzone na przyprostokątne.
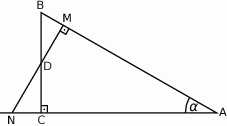
W trójkącie 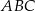 kąt przy wierzchołku
kąt przy wierzchołku 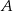 jest prosty, a kąt przy wierzchołku
jest prosty, a kąt przy wierzchołku 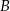 ma miarę
ma miarę 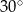 . Na boku
. Na boku 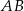 tego trójkąta obrano punkt
tego trójkąta obrano punkt 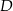 tak, że miara kąta
tak, że miara kąta 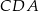 jest równa
jest równa 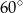 oraz
oraz 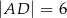 (zobacz rysunek). Oblicz
(zobacz rysunek). Oblicz 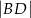 .
.
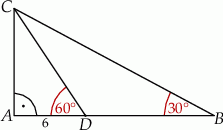
W trójkącie 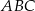 kąt przy wierzchołku
kąt przy wierzchołku 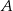 jest prosty, a kąt przy wierzchołku
jest prosty, a kąt przy wierzchołku 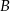 ma miarę
ma miarę 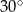 . Na boku
. Na boku 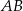 tego trójkąta obrano punkt
tego trójkąta obrano punkt 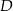 tak, że odcinek
tak, że odcinek 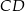 jest dwusieczną kąta przy wierzchołku
jest dwusieczną kąta przy wierzchołku 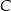 oraz
oraz 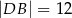 (zobacz rysunek). Oblicz
(zobacz rysunek). Oblicz 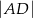 .
.
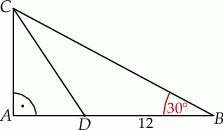
Przyprostokątna trójkąta prostokątnego ma długość 10. Miara kąta ostrego leżącego naprzeciw tej przyprostokątnej wynosi 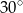 . Oblicz długość okręgu opisanego na tym trójkącie.
. Oblicz długość okręgu opisanego na tym trójkącie.
Przyprostokątna trójkąta prostokątnego ma długość 12. Miara kąta ostrego leżącego przy tej przyprostokątnej wynosi 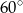 . Oblicz długość okręgu opisanego na tym trójkącie.
. Oblicz długość okręgu opisanego na tym trójkącie.
Na przedłużeniu przeciwprostokątnej 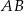 trójkąta prostokątnego
trójkąta prostokątnego 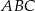 wybrano punkt
wybrano punkt 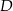 tak, że
tak, że 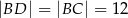 . Oblicz długość odcinka
. Oblicz długość odcinka 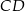 jeżeli
jeżeli 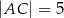 .
.
W trójkącie prostokątnym 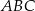 punkt
punkt 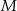 leży na przeciwprostokątnej
leży na przeciwprostokątnej 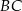 . Z punktu
. Z punktu 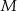 poprowadzono odcinki
poprowadzono odcinki 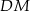 i
i 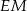 prostopadłe odpowiednio do przyprostokątnych
prostopadłe odpowiednio do przyprostokątnych 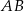 i
i 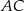 (rysunek).
(rysunek).
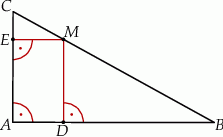
Udowodnij, że
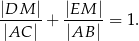
Trójkąt 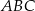 jest prostokątny. Z punktu
jest prostokątny. Z punktu 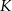 należącego do przeciwprostokątnej
należącego do przeciwprostokątnej 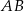 poprowadzono odcinki
poprowadzono odcinki 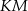 oraz
oraz 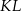 prostopadłe odpowiednio do przyprostokątnych
prostopadłe odpowiednio do przyprostokątnych 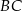 oraz
oraz 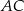 (rysunek).
(rysunek).
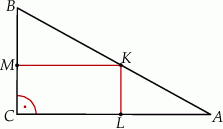
Wykaż, że
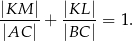
Na zewnątrz równoramiennego trójkąta prostokątnego zbudowano kwadraty – jeden na przyprostokątnej, a drugi na przeciwprostokątnej. Wykaż, że przeciwprostokątna dzieli odcinek łączący środki kwadratów na dwie równe części.
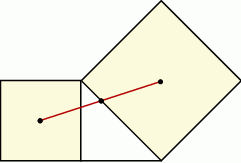
Trójkąt prostokątny ma boki długości 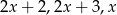 . Wyznacz
. Wyznacz  oraz promień okręgu wpisanego w ten trójkąt.
oraz promień okręgu wpisanego w ten trójkąt.
Wyznacz długość przeciwprostokątnej oraz miary kątów trójkąta prostokątnego, którego przyprostokątne mają długości 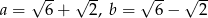 .
.
Przez środek 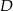 przyprostokątnej
przyprostokątnej 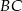 trójkąta prostokątnego
trójkąta prostokątnego 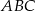 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 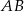 . Prosta ta przecina proste
. Prosta ta przecina proste 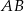 i
i 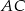 odpowiednio w punktach
odpowiednio w punktach 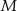 i
i 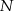 . Wykaż, że
. Wykaż, że 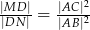 .
.
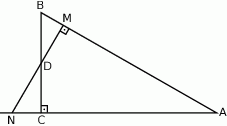
Wyznacz długości boków oraz miary kątów trójkąta prostokątnego 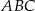 , jeżeli
, jeżeli 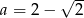 i
i 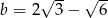 .
.