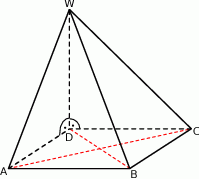
Podstawą ostrosłupa jest prostokąt, którego stosunek długości boków wynosi 2:3. Pole podstawy ostrosłupa jest równe 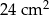 . Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem
. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 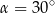 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny/Prostokąt w podstawie
Podstawą ostrosłupa jest prostokąt, którego stosunek długości boków wynosi 4:3. Pole podstawy ostrosłupa jest równe 48. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 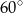 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Podstawą ostrosłupa 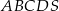 jest prostokąt
jest prostokąt 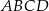 , w którym
, w którym 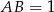 ,
, 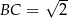 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz wartość dowolnej funkcji trygonometrycznej kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
. Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz wartość dowolnej funkcji trygonometrycznej kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
Podstawą ostrosłupa 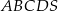 jest prostokąt
jest prostokąt 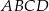 o bokach długości
o bokach długości  i
i 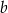 . Krawędź
. Krawędź 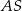 jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka
jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 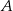 od krawędzi
od krawędzi 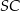 jest równa
jest równa 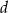 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.
Podstawą ostrosłupa 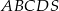 jest prostokąt
jest prostokąt 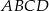 , a krawędź boczna
, a krawędź boczna 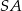 jest jego wysokością. Wykaż, że suma kwadratów pól ścian
jest jego wysokością. Wykaż, że suma kwadratów pól ścian 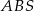 i
i 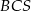 jest równa sumie kwadratów pól ścian
jest równa sumie kwadratów pól ścian 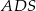 i
i 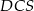 .
.
Podstawą ostrosłupa 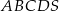 jest prostokąt, którego boki pozostają w stosunku 3:4, a pole jest równe 192 (zobacz rysunek). Punkt
jest prostokąt, którego boki pozostają w stosunku 3:4, a pole jest równe 192 (zobacz rysunek). Punkt 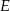 jest wyznaczony przez przecinające się przekątne podstawy, a odcinek
jest wyznaczony przez przecinające się przekątne podstawy, a odcinek 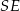 jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem
jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 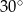 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
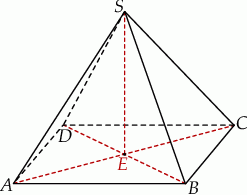
Podstawą ostrosłupa  jest prostokąt, którego boki pozostają w stosunku 5:12, a pole jest równe 240 (zobacz rysunek). Punkt
jest prostokąt, którego boki pozostają w stosunku 5:12, a pole jest równe 240 (zobacz rysunek). Punkt  jest wyznaczony przez przecinające się przekątne podstawy, a odcinek
jest wyznaczony przez przecinające się przekątne podstawy, a odcinek 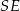 jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem
jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 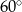 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
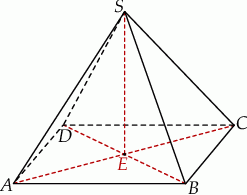
Podstawą ostrosłupa  jest prostokąt o polu równym 432, a stosunek długości boków tego prostokąta jest równy 3:4. Przekątne podstawy
jest prostokąt o polu równym 432, a stosunek długości boków tego prostokąta jest równy 3:4. Przekątne podstawy 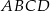 przecinają się w punkcie
przecinają się w punkcie 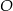 . Odcinek
. Odcinek 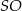 jest wysokością ostrosłupa (zobacz rysunek). Kąt
jest wysokością ostrosłupa (zobacz rysunek). Kąt 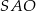 ma miarę
ma miarę 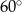 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
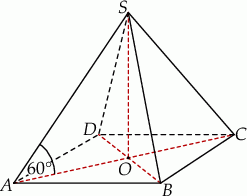
Podstawą ostrosłupa  jest prostokąt
jest prostokąt  , którego boki mają długości
, którego boki mają długości 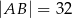 i
i 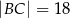 . Ściany boczne
. Ściany boczne 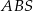 i
i 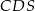 są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem
są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem  . Ściany boczne
. Ściany boczne 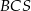 i
i 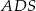 są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem
są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem 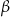 . Miary kątów
. Miary kątów  i
i 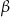 spełniają warunek:
spełniają warunek: 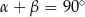 . Oblicz
. Oblicz 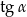 oraz pole powierzchni całkowitej tego ostrosłupa.
oraz pole powierzchni całkowitej tego ostrosłupa.
Podstawą ostrosłupa 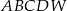 jest prostokąt
jest prostokąt 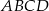 . Krawędź boczna
. Krawędź boczna 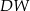 jest wysokością tego ostrosłupa. Krawędzie boczne
jest wysokością tego ostrosłupa. Krawędzie boczne 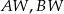 i
i 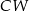 mają następujące długości:
mają następujące długości: 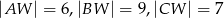 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 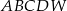 jest kwadrat
jest kwadrat 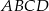 o polu 2. Krawędź boczna
o polu 2. Krawędź boczna 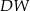 jest wysokością tego ostrosłupa. Długości krawędzi bocznych
jest wysokością tego ostrosłupa. Długości krawędzi bocznych 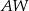 i
i 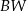 spełniają warunek
spełniają warunek 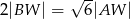 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
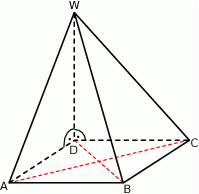
Podstawą ostrosłupa 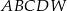 jest kwadrat
jest kwadrat 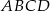 . Krawędź boczna
. Krawędź boczna 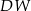 jest wysokością tego ostrosłupa. Krawędzie boczne
jest wysokością tego ostrosłupa. Krawędzie boczne 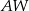 i
i 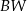 mają następujące długości:
mają następujące długości: 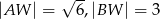 . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
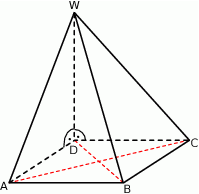
Podstawą ostrosłupa  jest prostokąt
jest prostokąt 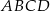 , w którym
, w którym 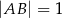 ,
, 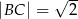 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
. Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
Podstawą ostrosłupa jest prostokąt o polu 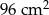 kwadratowych. Stosunek długości boków tego prostokąta wynosi 2:3. Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem
kwadratowych. Stosunek długości boków tego prostokąta wynosi 2:3. Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 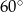 . Oblicz pole powierzchni całkowitej tej bryły.
. Oblicz pole powierzchni całkowitej tej bryły.
Podstawą ostrosłupa  jest prostokąt
jest prostokąt  . Spodkiem wysokości ostrosłupa jest środek
. Spodkiem wysokości ostrosłupa jest środek  krawędzi
krawędzi 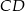 . Oblicz tangens kąta między ścianami bocznymi
. Oblicz tangens kąta między ścianami bocznymi 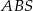 i
i 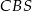 tego ostrosłupa jeżeli
tego ostrosłupa jeżeli 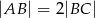 i
i 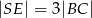 .
.
Podstawą ostrosłupa 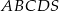 jest prostokąt
jest prostokąt 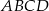 o bokach długości
o bokach długości 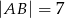 i
i 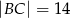 . Krawędź
. Krawędź 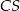 jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt
jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 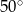 . Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
Podstawą ostrosłupa jest prostokąt o bokach 6 cm i 8 cm. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod katem 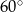 . Oblicz pole powierzchni ostrosłupa.
. Oblicz pole powierzchni ostrosłupa.

