Dziedziną funkcji 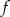 opisanej wzorem
opisanej wzorem 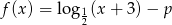 jest przedział
jest przedział 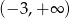 . Wiedząc, że do wykresu funkcji
. Wiedząc, że do wykresu funkcji 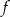 należy punkt
należy punkt 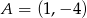 , oblicz wartość parametru
, oblicz wartość parametru 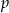 . Następnie:
. Następnie:
- naszkicuj wykres funkcji
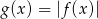 ;
; - wyznacz zbiór wszystkich wartości parametru
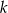 , dla których równanie
, dla których równanie 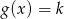 ma dwa rozwiązania różnych znaków.
ma dwa rozwiązania różnych znaków.

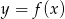 przesunięto równolegle do osi
przesunięto równolegle do osi 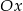 o 5 jednostek w prawo i równolegle do osi
o 5 jednostek w prawo i równolegle do osi 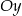 o 2 jednostki w dół. Podaj wzór funkcji:
o 2 jednostki w dół. Podaj wzór funkcji: 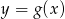 będącej obrazem wykresu funkcji
będącej obrazem wykresu funkcji 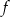 w przesunięciu, jeżeli
w przesunięciu, jeżeli 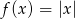 . Narysuj wykres funkcji
. Narysuj wykres funkcji 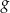 .
. 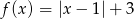 określonej dla
określonej dla 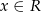 , a następnie na jego podstawie podaj liczbę rozwiązań równania
, a następnie na jego podstawie podaj liczbę rozwiązań równania 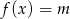 w zależności od parametru
w zależności od parametru 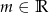 .
. 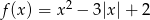 .
. 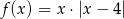 .
. 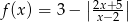 .
. 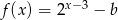 , określonej dla
, określonej dla 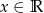 .
. 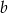 .
. 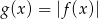 .
. 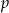 , dla których równanie
, dla których równanie 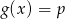 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.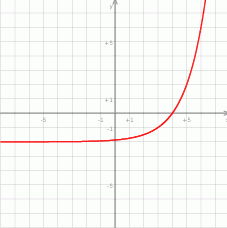
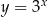 przekształcono i otrzymano wykres funkcji
przekształcono i otrzymano wykres funkcji 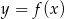 (rys).
(rys). 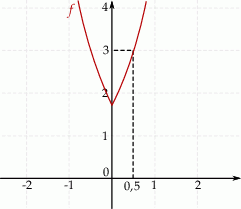
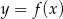 , a następnie zaznacz na płaszczyźnie zbiór
, a następnie zaznacz na płaszczyźnie zbiór ![{ } A = x,y : x ∈ R i y ∈ R i log(x−1)2+y 2[log 9f2(x)] < 0 .](https://img.zadania.info/zad/2686807/HzadT4x.gif)
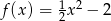 .
. 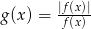 , której dziedziną jest zbiór
, której dziedziną jest zbiór 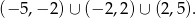
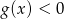 .
.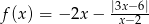 .
. 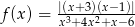 .
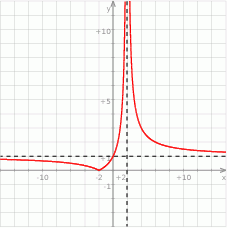
. 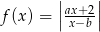 .
. 
 i
i 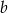 .
. 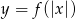 .
. 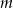 , dla których równanie
, dla których równanie 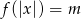 ma cztery rozwiązania.
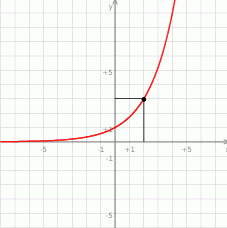
ma cztery rozwiązania.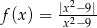 . Określ dziedzinę oraz zbiór wartości funkcji.
. Określ dziedzinę oraz zbiór wartości funkcji. 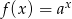 dla
dla 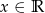 .
. 
 .
. 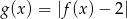 i podaj wszystkie wartości parametru
i podaj wszystkie wartości parametru 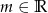 , dla których równanie
, dla których równanie 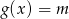 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.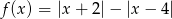 , na podstawie wykresu określ liczbę rozwiązań równania
, na podstawie wykresu określ liczbę rozwiązań równania 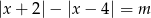 w zależności od parametru
w zależności od parametru 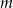 .
. 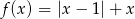 .
. 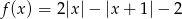 .
. 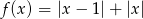 .
. 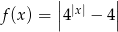 . Na podstawie wykresu określ przedziały, w których funkcja jest rosnącą.
. Na podstawie wykresu określ przedziały, w których funkcja jest rosnącą. 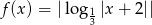 .
. 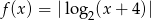 .
. 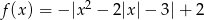 ;
; 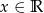 .
. 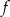 określ zbiór wartości tej funkcji.
określ zbiór wartości tej funkcji. 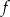 .
. 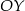 .
. 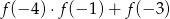 .
. 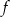 określonej wzorem
określonej wzorem 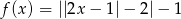 . Podaj miejsca zerowe tej funkcji oraz jej zbiór wartości.
. Podaj miejsca zerowe tej funkcji oraz jej zbiór wartości. 