Przekrój ostrosłupa prawidłowego czworokątnego zawierającego przekątną podstawy oraz wierzchołek ostrosłupa jest trójkątem równobocznym o polu 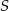 . Oblicz objętość tego ostrosłupa . Wykonaj rysunek pomocniczy.
. Oblicz objętość tego ostrosłupa . Wykonaj rysunek pomocniczy.
/Szkoła średnia/Geometria/Stereometria
Ostrosłup 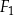 jest podobny do ostrosłupa
jest podobny do ostrosłupa 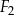 . Objętość ostrosłupa
. Objętość ostrosłupa 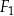 jest równa 64, a objętość ostrosłupa
jest równa 64, a objętość ostrosłupa 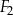 jest równa 512. Oblicz stosunek pola powierzchni całkowitej ostrosłupa
jest równa 512. Oblicz stosunek pola powierzchni całkowitej ostrosłupa 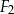 do pola powierzchni całkowitej ostrosłupa
do pola powierzchni całkowitej ostrosłupa 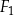 .
.
Podstawą ostrosłupa 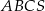 jest trójkąt
jest trójkąt 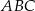 , w którym
, w którym 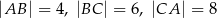 . Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt
. Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt 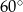 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Podstawą ostrosłupa jest trójkąt prostokątny, w którym tangens jednego z kątów ostrych jest równy 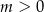 . Wszystkie krawędzie boczne ostrosłupa mają długość
. Wszystkie krawędzie boczne ostrosłupa mają długość 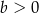 . Jakie powinno być pole podstawy ostrosłupa, aby jego objętość była największa? Oblicz tę największą objętość.
. Jakie powinno być pole podstawy ostrosłupa, aby jego objętość była największa? Oblicz tę największą objętość.
W dwudziestościanie foremnym odcięto płaszczyznami przechodzącymi przez środki krawędzi każdy z narożników. Ile ścian ma powstała w ten sposób bryła i jakimi są one wielokątami?
Podstawą ostrosłupa prawidłowego trójkątnego 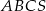 jest trójkąt
jest trójkąt 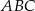 . Punkty
. Punkty 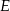 i
i 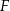 są rzutami punktów
są rzutami punktów 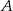 i
i 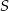 na przeciwległe ściany. Oblicz w jakim stosunku odcinek
na przeciwległe ściany. Oblicz w jakim stosunku odcinek 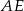 dzieli odcinek
dzieli odcinek 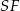 , jeżeli ściana boczna ostrosłupa jest nachylona do podstawy pod kątem, którego sinus jest równy
, jeżeli ściana boczna ostrosłupa jest nachylona do podstawy pod kątem, którego sinus jest równy  .
.
Rozpatrujemy wszystkie stożki, których pole powierzchni całkowitej jest równe 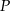 . Oblicz wysokość i promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
. Oblicz wysokość i promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
Do naczynia w kształcie walca wypełnionego wodą do wysokości 7 cm włożono metalową kulkę o promieniu 3 cm. Poziom wody podniósł się o 1 cm i zrównał się z górną podstawą walca. Oblicz objętość naczynia. Przyjmując 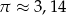 , wynik podaj z dokładnością do
, wynik podaj z dokładnością do 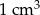 .
.
Rozpatrujemy wszystkie walce, których pole powierzchni całkowitej jest równe 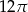 . Wyznacz wysokość tego spośród rozpatrywanych walców, którego objętość jest największa. Oblicz tę objętość.
. Wyznacz wysokość tego spośród rozpatrywanych walców, którego objętość jest największa. Oblicz tę objętość.
Rozpatrujemy wszystkie walce, których pole powierzchni całkowitej jest równe 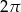 . Oblicz promień podstawy tego walca, który ma największą objętość. Podaj tę największą objętość.
. Oblicz promień podstawy tego walca, który ma największą objętość. Podaj tę największą objętość.
Podstawą ostrosłupa 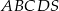 jest prostokąt
jest prostokąt 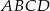 . Spodkiem wysokości ostrosłupa jest środek
. Spodkiem wysokości ostrosłupa jest środek 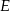 krawędzi
krawędzi 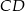 . Oblicz tangens kąta między ścianami bocznymi
. Oblicz tangens kąta między ścianami bocznymi 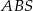 i
i 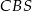 tego ostrosłupa jeżeli
tego ostrosłupa jeżeli 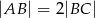 i
i 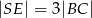 .
.
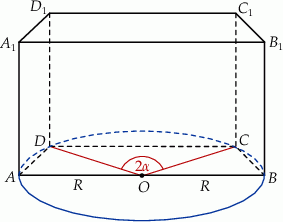
Podstawą graniastosłupa prostego 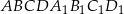 jest trapez równoramienny
jest trapez równoramienny 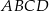 wpisany w okrąg o środku
wpisany w okrąg o środku 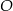 i promieniu
i promieniu 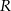 . Dłuższa podstawa
. Dłuższa podstawa 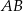 trapezu jest średnicą tego okręgu, a krótsza – cięciwą odpowiadającą kątowi środkowemu o mierze
trapezu jest średnicą tego okręgu, a krótsza – cięciwą odpowiadającą kątowi środkowemu o mierze 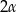 (zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze
(zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze  . Wyznacz objętość tego graniastosłupa jako funkcję promienia
. Wyznacz objętość tego graniastosłupa jako funkcję promienia 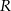 i miary kąta
i miary kąta  .
.
Rozważamy wszystkie graniastosłupy prawidłowe trójkątne o objętości 3456, których krawędź podstawy ma długość nie większą niż 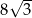 .
.
-
Wykaż, że pole
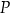 powierzchni całkowitej graniastosłupa w zależności od długości
powierzchni całkowitej graniastosłupa w zależności od długości  krawędzi podstawy graniastosłupa jest określone wzorem
krawędzi podstawy graniastosłupa jest określone wzorem 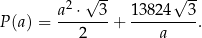
-
Wyznacz długość krawędzi podstawy tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
W ostrosłupie prawidłowym czworokątnym ściana boczna o polu równym 10 jest nachylona do płaszczyzny podstawy pod kątem 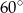 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 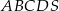 jest trapez równoramienny
jest trapez równoramienny 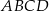 , którego ramiona mają długość
, którego ramiona mają długość 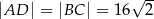 i tworzą z podstawą
i tworzą z podstawą 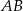 kąt ostry o mierze
kąt ostry o mierze 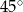 . Każda ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod tym samym kątem
. Każda ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod tym samym kątem  takim, że
takim, że 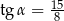 . Oblicz odległość spodka wysokości tego ostrosłupa od jego ściany bocznej
. Oblicz odległość spodka wysokości tego ostrosłupa od jego ściany bocznej 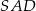 .
.
Podstawą ostrosłupa czworokątnego 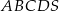 jest trapez
jest trapez 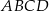 (
(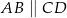 ). Ramiona tego trapezu mają długości
). Ramiona tego trapezu mają długości 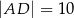 i
i 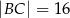 , a miara kąta
, a miara kąta 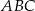 jest równa
jest równa 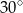 . Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt
. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt  , taki, że
, taki, że 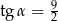 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 2, a krawędź boczna długość 6.
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź boczna ma długość 8, a krawędź podstawy ma długość 2.
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 4, a krawędź boczna długość 10.
W ostrosłupie prawidłowym czworokątnym 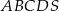 o podstawie
o podstawie 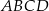 wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 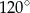 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 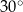 i ma długość równą 6 (zobacz rysunek).
i ma długość równą 6 (zobacz rysunek).
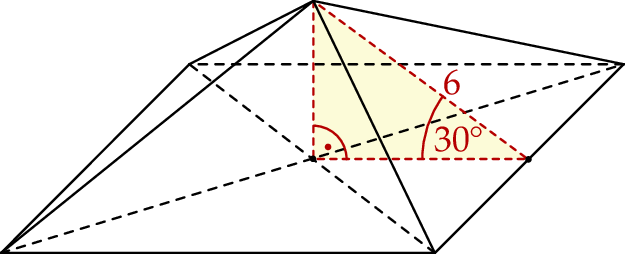
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 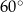 i ma długość równą 6 (zobacz rysunek).
i ma długość równą 6 (zobacz rysunek).
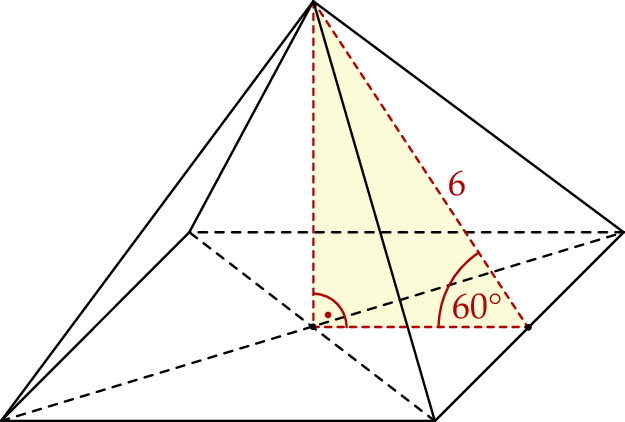
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny. Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 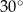 , a krawędź podstawy ma długość równą
, a krawędź podstawy ma długość równą 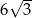 . Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
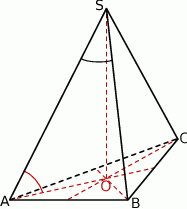
Podstawą ostrosłupa prawidłowego trójkątnego 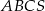 jest trójkąt
jest trójkąt 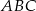 . Kąt nachylenia krawędzi bocznej
. Kąt nachylenia krawędzi bocznej 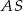 do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi
do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi 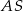 i
i 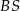 zawartymi w ścianie bocznej
zawartymi w ścianie bocznej 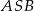 tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.
tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.
Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę 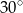 . Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
. Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
Dany jest prostopadłościan o polu powierzchni równym 162, w którym przekątna jest liczbą z przedziału 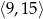 . Wykaż, że suma długości wszystkich krawędzi tego prostopadłościanu jest liczbą z przedziału
. Wykaż, że suma długości wszystkich krawędzi tego prostopadłościanu jest liczbą z przedziału 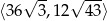 .
.

