Metalową kulę o promieniu 10 cm i stożek o średnicy 16 cm i wysokości 12 cm przetopiono. Następnie z otrzymanego metalu wykonano walec o średnicy 8 cm. Jaką wysokość ma ten walec?
/Szkoła średnia/Geometria/Stereometria
Metalową kulę o promieniu 5 cm i stożek o średnicy 12 cm i wysokości 15 cm przetopiono. Następnie z otrzymanego metalu wykonano walec o średnicy 8 cm. Jaką wysokość ma ten walec?
Przekrój stożka wyznaczony przez wierzchołek i cięciwę podstawy jest trójkątem równobocznym, o polu równym 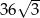 . Płaszczyzna
. Płaszczyzna  , do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej
, do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej 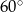 . Oblicz objętość stożka.
. Oblicz objętość stożka.
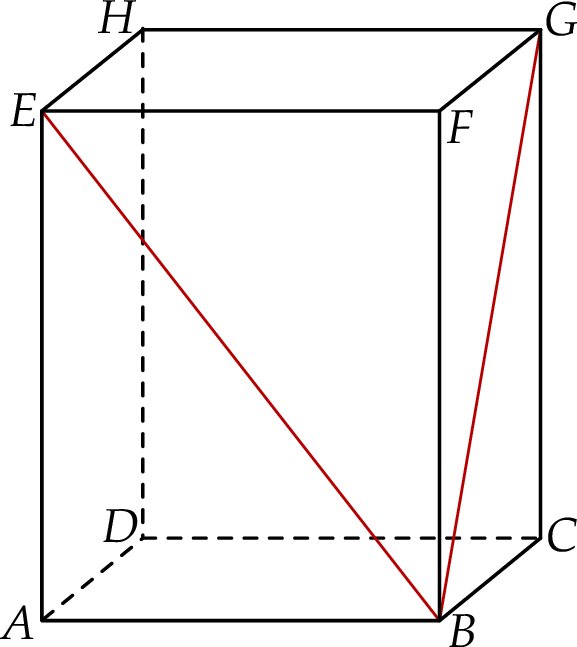
Dany jest sześcian 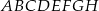 , w którym
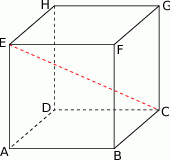
, w którym 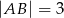 (patrz rysunek). Oblicz odległość wierzchołka
(patrz rysunek). Oblicz odległość wierzchołka 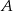 od przekątnej
od przekątnej 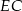 .
.
Cosinus kąta rozwarcia stożka jest równy 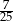 . Odległość środka kuli wpisanej w ten stożek od jego wierzchołka jest równa 10. Oblicz pole powierzchni bocznej stożka.
. Odległość środka kuli wpisanej w ten stożek od jego wierzchołka jest równa 10. Oblicz pole powierzchni bocznej stożka.
Trapez prostokątny o podstawach długości 4 i 5 oraz kącie ostrym równym 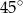 obraca się wokół krótszej podstawy. Oblicz objętość otrzymanej bryły.
obraca się wokół krótszej podstawy. Oblicz objętość otrzymanej bryły.
Rozwinięcie powierzchni bocznej stożka jest wycinkiem kołowym o kącie środkowym  . Kąt ten oparty jest na łuku długości
. Kąt ten oparty jest na łuku długości  . Oblicz objętość stożka.
. Oblicz objętość stożka.
Niech 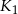 będzie sześcianem o krawędzi długości
będzie sześcianem o krawędzi długości  . Konstruujemy kolejno sześciany
. Konstruujemy kolejno sześciany 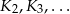 takie, że pole powierzchni całkowitej kolejnego sześcianu jest dwa razy większe od pola powierzchni poprzedniego sześcianu. Oblicz sumę objętości sześcianów
takie, że pole powierzchni całkowitej kolejnego sześcianu jest dwa razy większe od pola powierzchni poprzedniego sześcianu. Oblicz sumę objętości sześcianów 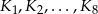 .
.
Podstawą ostrosłupa 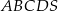 jest prostokąt
jest prostokąt 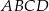 o bokach długości
o bokach długości  i
i 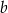 . Krawędź
. Krawędź 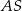 jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka
jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 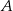 od krawędzi
od krawędzi 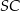 jest równa
jest równa 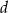 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.
W prostopadłościanie 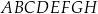 przekątna ściany
przekątna ściany 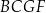 jest o 2 dłuższa od krawędzi
jest o 2 dłuższa od krawędzi 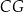 i o 4 dłuższa od krawędzi
i o 4 dłuższa od krawędzi 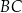 . Przekątna ściany
. Przekątna ściany 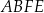 jest nachylona do płaszczyzny
jest nachylona do płaszczyzny 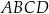 pod kątem
pod kątem 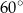 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Podstawą graniastosłupa prostego 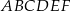 jest trójkąt równoramienny
jest trójkąt równoramienny 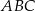 , w którym
, w którym 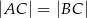 ,
, 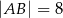 . Wysokość trójkąta
. Wysokość trójkąta 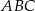 , poprowadzona z wierzchołka
, poprowadzona z wierzchołka 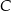 , ma długość 3. Przekątna
, ma długość 3. Przekątna 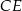 ściany bocznej tworzy z krawędzią
ściany bocznej tworzy z krawędzią 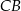 podstawy
podstawy 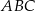 kąt
kąt 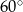 (zobacz rysunek).
(zobacz rysunek).
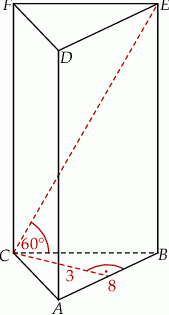
Oblicz pole powierzchni całkowitej oraz objętość tego graniastosłupa.
Podstawą graniastosłupa prostego jest trójkąt prostokątny równoramienny. Kąt między przekątnymi, wychodzącymi z tego samego wierzchołka, dwóch prostopadłych ścian bocznych, ma miarę 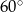 . Wiedząc, że objętość tego graniastosłupa jest równa
. Wiedząc, że objętość tego graniastosłupa jest równa 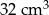 , oblicz pole powierzchni całkowitej tej bryły.
, oblicz pole powierzchni całkowitej tej bryły.
Oblicz objętość graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 16 cm i 30 cm, a krawędź boczna jest dwa razy dłuższa od krawędzi podstawy.
W kostce mającej kształt sześcianu o boku 1 dm ścięto wszystkie naroża w ten sposób ze wszystkie krawędzie nowopowstałej bryły mają tę samą długość. Obliczyć objętość otrzymanej bryły.
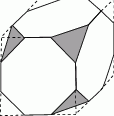
W kulę o promieniu 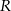 wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem
wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem  . Oblicz objętość stożka.
. Oblicz objętość stożka.
Trójkąt równoramienny o obwodzie 12 obraca się wokół swojej osi symetrii. Oblicz dla jakich długości boków trójkąta otrzymamy stożek, w którym różnica między polem powierzchni bocznej, a polem podstawy jest największa. Oblicz objętość tego stożka.
W czworościanie 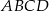 krawędź
krawędź 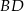 ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
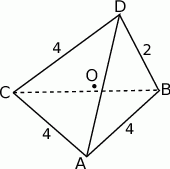
- Oblicz odległość krawędzi
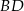 od krawędzi
od krawędzi 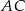 .
. - Wiedząc, że punkt
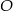 jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka
jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka 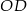 .
.
Trójkąt równoramienny o podstawie długości 6 cm i ramionach długości 5 cm obracamy wokół jednego z ramion. Otrzymaną w ten sposób bryłę dzielimy na dwa stożki. Podaj długość promienia podstawy i długość tworzącej każdego z tych stożków.
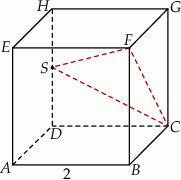
Dany jest sześcian 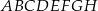 o krawędzi długości 2. Punkt
o krawędzi długości 2. Punkt 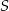 jest środkiem krawędzi
jest środkiem krawędzi 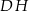 (zobacz rysunek). Oblicz miarę najmniejszego kąta wewnętrznego trójkąta
(zobacz rysunek). Oblicz miarę najmniejszego kąta wewnętrznego trójkąta 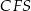 .
.
Dany jest graniastosłup prawidłowy trójkątny 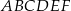 . Krawędź podstawy tego graniastosłupa ma długość 4, a wysokość graniastosłupa jest równa 6 (zobacz rysunek).
. Krawędź podstawy tego graniastosłupa ma długość 4, a wysokość graniastosłupa jest równa 6 (zobacz rysunek).
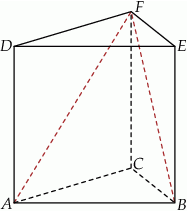
Oblicz sinus kąta 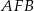 .
.
Punkty 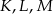 i
i 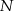 są środkami krawędzi
są środkami krawędzi 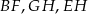 i
i 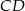 prostopadłościanu
prostopadłościanu 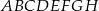 , w którym
, w którym 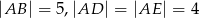 . Uzasadnij, że
. Uzasadnij, że 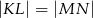 .
.