Dany jest sześcian 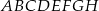 . Przez wierzchołki
. Przez wierzchołki 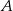 i
i 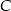 oraz środek
oraz środek 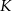 krawędzi
krawędzi 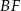 poprowadzono płaszczyznę, która przecina przekątną
poprowadzono płaszczyznę, która przecina przekątną 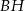 w punkcie
w punkcie 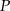 (zobacz rysunek).
(zobacz rysunek).
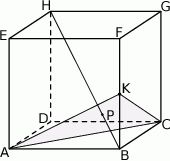
Wykaż, że 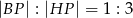 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest sześcian 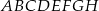 . Przez wierzchołki
. Przez wierzchołki 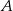 i
i 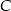 oraz środek
oraz środek 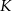 krawędzi
krawędzi 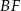 poprowadzono płaszczyznę, która przecina przekątną
poprowadzono płaszczyznę, która przecina przekątną 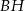 w punkcie
w punkcie 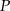 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że 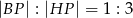 .
.
Dany jest sześcian  . Przez wierzchołki
. Przez wierzchołki 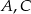 oraz
oraz 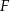 poprowadzono płaszczyznę, która przecina przekątną
poprowadzono płaszczyznę, która przecina przekątną 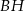 w punkcie
w punkcie 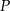 (zobacz rysunek).
(zobacz rysunek).
Wykaż, że 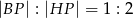 .
.
Powierzchnia boczna stożka jest wycinkiem kołowym, którego kąt środkowy ma miarę 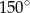 . Wiedząc, że tworząca stożka ma długość 24 cm, oblicz pole powierzchni bocznej i objętość tego stożka.
. Wiedząc, że tworząca stożka ma długość 24 cm, oblicz pole powierzchni bocznej i objętość tego stożka.
Powierzchnia boczna stożka jest wycinkiem kołowym, którego kąt środkowy ma miarę 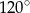 . Wiedząc, że tworząca stożka ma długość 12 cm, oblicz pole powierzchni bocznej i objętość tego stożka.
. Wiedząc, że tworząca stożka ma długość 12 cm, oblicz pole powierzchni bocznej i objętość tego stożka.
W ostrosłupie prawidłowym czworokątnym krawędź boczna tworzy z krawędzią podstawy kąta  . Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi.
. Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi.
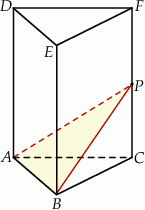
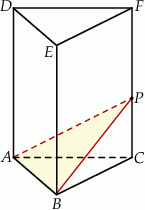
Dany jest graniastosłup prawidłowy trójkątny 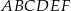 o podstawach
o podstawach 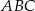 i
i 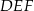 i krawędziach bocznych
i krawędziach bocznych 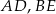 i
i 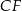 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 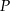 jest środkiem krawędzi
jest środkiem krawędzi 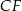 . Długość krawędzi podstawy
. Długość krawędzi podstawy 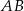 jest równa 12, a pole trójkąta
jest równa 12, a pole trójkąta 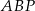 jest równe
jest równe 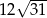 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Krawędź podstawy graniastosłupa prawidłowego trójkątnego  jest równa 6 (zobacz rysunek). Punkt
jest równa 6 (zobacz rysunek). Punkt  dzieli krawędź boczną
dzieli krawędź boczną  w stosunku
w stosunku 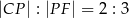 . Pole trójkąta
. Pole trójkąta  jest równe
jest równe  . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
W sferę o promieniu 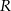 wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość
wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość 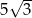 , oblicz
, oblicz 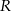 .
.
Wysokość prostopadłościanu 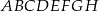 jest równa 1, a długość przekątnej
jest równa 1, a długość przekątnej 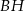 jest równa sumie długości krawędzi
jest równa sumie długości krawędzi 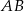 i
i 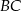 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Wysokość walca wpisanego w stożek jest równa promieniowi podstawy stożka. Stosunek objętości stożka do objętości walca wynosi 8 : 3. Oblicz tangens kąta zawartego między wysokością a tworzącą stożka.
Podstawą prostopadłościanu jest kwadrat o boku długości 4, a wysokość prostopadłościanu jest równa 8. Połączono odcinkami środki trzech krawędzi prostopadłościanu, z których żadne dwie nie leżą w jednej płaszczyźnie, i otrzymano trójkąt 
 .
.  .
.Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 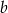 i tworzy z krawędzią podstawy kąt o mierze
i tworzy z krawędzią podstawy kąt o mierze  . Jaką objętość ma ten ostrosłup?
. Jaką objętość ma ten ostrosłup?
Z czterech ołowianych sześcianów o przekątnej długości 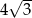 wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
Czworościan foremny przecięto płaszczyzną przechodzącą przez krawędź boczną i wysokość podstawy. Jako przekrój otrzymano trójkąt o polu równym 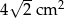 . Oblicz objętość tego czworościanu.
. Oblicz objętość tego czworościanu.
Rozpatrujemy wszystkie trójkąty równoramienne o ramionach długości 6. Oblicz cosinus kąta między ramionami tego z tych trójkątów, dla którego objętość bryły powstałej w wyniku obrotu trójkąta dokoła prostej zawierającej jego podstawę jest największa możliwa. Oblicz tę największą objętość.
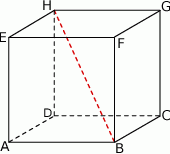
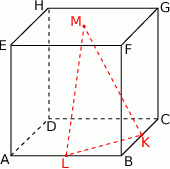
Punkty 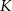 i
i 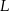 są środkami krawędzi
są środkami krawędzi 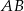 i
i 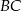 sześcianu
sześcianu 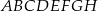 o krawędzi długości 1. Punkt
o krawędzi długości 1. Punkt 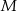 jest środkiem ściany
jest środkiem ściany  (zobacz rysunek). Oblicz pole trójkąta
(zobacz rysunek). Oblicz pole trójkąta  .
.
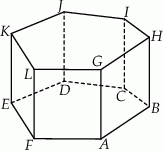
Dany jest graniastosłup prosty o podstawie pięciokątnej  (zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu dwa razy mniejszym niż pole pięciokąta
(zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu dwa razy mniejszym niż pole pięciokąta  . Pole powierzchni całkowitej tego graniastosłupa jest równe 153. Oblicz jego objętość.
. Pole powierzchni całkowitej tego graniastosłupa jest równe 153. Oblicz jego objętość.
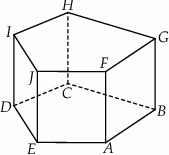
Dany jest graniastosłup prosty o podstawie sześciokątnej  (zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu o 25% mniejszym niż pole sześciokąta
(zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu o 25% mniejszym niż pole sześciokąta  . Pole powierzchni całkowitej tego graniastosłupa jest równe 156. Oblicz jego objętość.
. Pole powierzchni całkowitej tego graniastosłupa jest równe 156. Oblicz jego objętość.
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 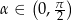 , a krawędź podstawy ma długość
, a krawędź podstawy ma długość  . Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt
. Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt 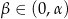 . Wykaż, że pole otrzymanego przekroju jest równe
. Wykaż, że pole otrzymanego przekroju jest równe
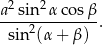
Podstawą ostrosłupa 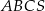 jest trójkąt równoboczny
jest trójkąt równoboczny 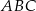 o boku długości 8. Punkt
o boku długości 8. Punkt 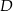 jest środkiem krawędzi
jest środkiem krawędzi 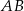 , odcinek
, odcinek 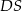 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 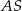 i
i 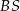 mają długość 7. Oblicz długość krawędzi
mają długość 7. Oblicz długość krawędzi 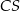 tego ostrosłupa.
tego ostrosłupa.
Podstawą ostrosłupa 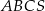 jest trójkąt równoboczny
jest trójkąt równoboczny 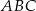 o boku długości 6. Punkt
o boku długości 6. Punkt 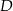 jest środkiem krawędzi
jest środkiem krawędzi 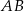 , odcinek
, odcinek 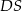 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 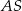 i
i 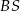 mają długość
mają długość 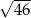 . Oblicz długość krawędzi
. Oblicz długość krawędzi 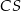 tego ostrosłupa.
tego ostrosłupa.
Podstawą ostrosłupa 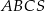 jest trójkąt równoboczny
jest trójkąt równoboczny 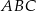 o boku długości 6. Punkt
o boku długości 6. Punkt 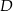 jest środkiem krawędzi
jest środkiem krawędzi 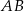 , odcinek
, odcinek 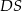 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 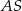 i
i 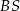 mają długość 8. Oblicz długość krawędzi
mają długość 8. Oblicz długość krawędzi 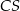 tego ostrosłupa.
tego ostrosłupa.
W graniastosłupie prawidłowym czworokątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu 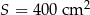 . Oblicz objętość i pole powierzchni całkowitej tej bryły .
. Oblicz objętość i pole powierzchni całkowitej tej bryły .
W graniastosłupie prawidłowym trójkątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu 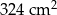 . Oblicz objętość tej bryły .
. Oblicz objętość tej bryły .
Podstawą ostrosłupa 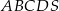 jest czworokąt wypukły
jest czworokąt wypukły 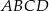 , w którym
, w którym 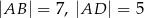 oraz
oraz 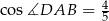 . Każda z krawędzi bocznych ostrosłupa ma długość
. Każda z krawędzi bocznych ostrosłupa ma długość 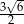 . Oblicz wysokość ostrosłupa.
. Oblicz wysokość ostrosłupa.
Podstawą ostrosłupa 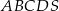 jest czworokąt wypukły
jest czworokąt wypukły 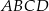 , w którym
, w którym 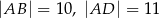 oraz
oraz 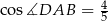 . Każda z krawędzi bocznych ostrosłupa ma długość 6. Oblicz wysokość ostrosłupa.
. Każda z krawędzi bocznych ostrosłupa ma długość 6. Oblicz wysokość ostrosłupa.
Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości  . Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Uzasadnij, że wysokość graniastosłupa jest nie większa niż
. Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Uzasadnij, że wysokość graniastosłupa jest nie większa niż 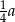 .
.
Oblicz długość przeciwprostokątnej trójkąta prostokątnego, wiedząc, że objętość brył powstałych z obrotu tego trójkąta wokół przyprostokątnych wynoszą odpowiednio 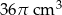 i
i 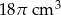 .
.
