W metalowym ostrosłupie prawidłowym czworokątnym o wysokości 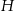 i krawędzi podstawy
i krawędzi podstawy  wydrążono otwór w kształcie walca, którego oś symetrii pokrywa się z osią symetrii ostrosłupa (patrz rysunek). Otwór wydrążono przez podstawę ostrosłupa w ten sposób, że górna podstawa walca nie wystaje poza powierzchnię ostrosłupa. Jaka może być najmniejsza możliwa objętość otrzymanej w ten sposób bryły?
wydrążono otwór w kształcie walca, którego oś symetrii pokrywa się z osią symetrii ostrosłupa (patrz rysunek). Otwór wydrążono przez podstawę ostrosłupa w ten sposób, że górna podstawa walca nie wystaje poza powierzchnię ostrosłupa. Jaka może być najmniejsza możliwa objętość otrzymanej w ten sposób bryły?

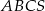 o wierzchołku
o wierzchołku 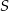 mają długość
mają długość 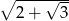 . Wiedząc, że
. Wiedząc, że 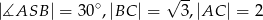 oblicz objętość tego ostrosłupa.
oblicz objętość tego ostrosłupa.  , którego podstawą jest trójkąt
, którego podstawą jest trójkąt 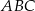 o kątach
o kątach 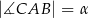 i
i 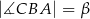 . Przekątne
. Przekątne 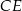 i
i 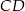 ścian bocznych tworzą kąt o mierze
ścian bocznych tworzą kąt o mierze 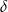 takiej, że
takiej, że 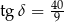 (zobacz rysunek).
(zobacz rysunek). 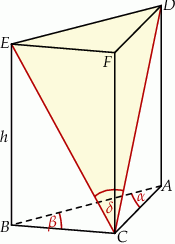
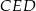 jest równe 4, a pole trójkąta
jest równe 4, a pole trójkąta 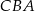 jest równe
jest równe 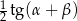 . Oblicz wysokość
. Oblicz wysokość 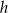 tego graniastosłupa.
tego graniastosłupa. 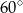 .
. 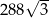 . Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze
. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
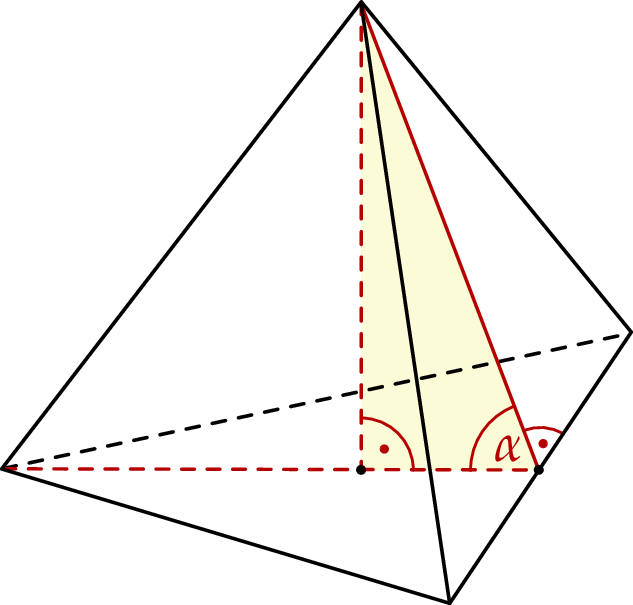
taki, że 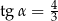 .
. 
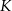 i
i 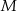 są środkami krawędzi
są środkami krawędzi 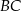 i
i 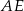 sześcianu
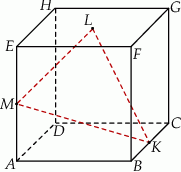
sześcianu 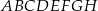 o krawędzi długości 1. Punkt
o krawędzi długości 1. Punkt 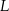 jest środkiem ściany
jest środkiem ściany 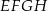 (zobacz rysunek). Oblicz obwód trójkąta
(zobacz rysunek). Oblicz obwód trójkąta 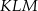 .
. 
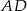 podstawy
podstawy 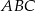 ostrosłupa trójkątnego
ostrosłupa trójkątnego 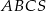 wybrano punkty
wybrano punkty 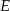 i
i 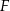 w ten sposób, że
w ten sposób, że 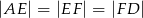 . Przez punkty
. Przez punkty 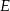 i
i 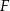 poprowadzono płaszczyzny równoległe do ściany
poprowadzono płaszczyzny równoległe do ściany 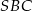 . Oblicz stosunek pól otrzymanych w ten sposób przekrojów ostrosłupa.
. Oblicz stosunek pól otrzymanych w ten sposób przekrojów ostrosłupa. 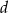 tworzy z odpowiednimi ścianami bocznymi kąty o miarach
tworzy z odpowiednimi ścianami bocznymi kąty o miarach  i
i 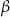 . Wyznacz objętość tego prostopadłościanu.
. Wyznacz objętość tego prostopadłościanu. 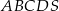 jest prostokąt
jest prostokąt 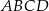 , w którym
, w którym 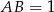 ,
, 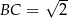 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz wartość dowolnej funkcji trygonometrycznej kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
. Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz wartość dowolnej funkcji trygonometrycznej kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.  . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa. 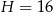 . Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
. Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy  . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa. 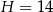 . Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
. Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy  . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.  . Przez wierzchołek ostrosłupa i środki dwóch sąsiednich krawędzi podstawy poprowadzono płaszczyznę . Wyznacz sinus kąta nachylenia wyznaczonego przekroju do podstawy ostrosłupa.
. Przez wierzchołek ostrosłupa i środki dwóch sąsiednich krawędzi podstawy poprowadzono płaszczyznę . Wyznacz sinus kąta nachylenia wyznaczonego przekroju do podstawy ostrosłupa. 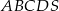 jest kwadrat
jest kwadrat 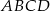 . Trójkąt równoramienny
. Trójkąt równoramienny 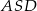 ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź
ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 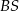 ma długość 17. Oblicz cosinus kąta nachylenia płaszczyzny
ma długość 17. Oblicz cosinus kąta nachylenia płaszczyzny 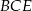 do płaszczyzny podstawy, gdzie
do płaszczyzny podstawy, gdzie 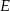 jest środkiem krawędzi
jest środkiem krawędzi 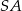 .
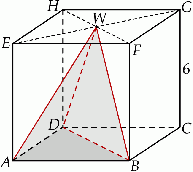
. 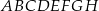 o krawędzi długości 6. Wierzchołki
o krawędzi długości 6. Wierzchołki 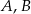 i
i 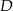 podstawy
podstawy 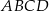 sześcianu połączono odcinkami z punktem
sześcianu połączono odcinkami z punktem 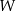 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy 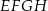 . Otrzymano w ten sposób ostrosłup trójkątny
. Otrzymano w ten sposób ostrosłup trójkątny 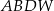 .
. 
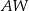 i
i 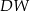 ostrosłupa.
ostrosłupa.  , dla którego
, dla którego 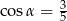 . Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa.
. Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa.  , dla którego
, dla którego 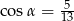 . Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa.
. Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa. 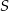 . Kąt płaski przy wierzchołku ostrosłupa ma miarę
. Kąt płaski przy wierzchołku ostrosłupa ma miarę 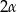 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 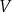 każdego z rozpatrywanych prostopadłościanów można wyrazić za pomocą funkcji
każdego z rozpatrywanych prostopadłościanów można wyrazić za pomocą funkcji 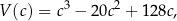
![[ ] c ∈ 4, 238](https://img.zadania.info/zad/2512356/HzadT2x.png) jest długością jednej z krawędzi bryły. Oblicz objętość tego spośród rozpatrywanych prostopadłościanów, którego objętość jest najmniejsza.
jest długością jednej z krawędzi bryły. Oblicz objętość tego spośród rozpatrywanych prostopadłościanów, którego objętość jest najmniejsza. 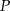 wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu. 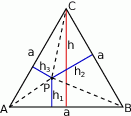
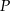 z wierzchołkami trójkąta i zapisujemy równość pól
z wierzchołkami trójkąta i zapisujemy równość pól 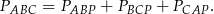
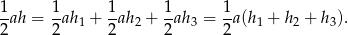
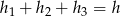 , a więc suma ta nie zależy od wyboru punktu
, a więc suma ta nie zależy od wyboru punktu 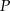 .
.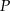 wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu
wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu 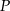 .
. 