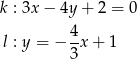Określ wzajemne położenie prostych 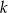 i
i 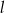 o równaniach
o równaniach
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Określ wzajemne położenie prostych 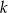 i
i 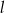 o równaniach
o równaniach
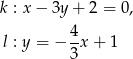
Dane są punkty 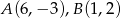 oraz
oraz 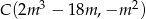 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 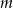 , dla których proste
, dla których proste 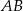 i
i 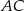 są prostopadłe.
są prostopadłe.
Dana jest prosta 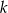 o równaniu parametrycznym
o równaniu parametrycznym 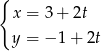 dla
dla 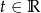 . Znajdź równanie parametryczne:
. Znajdź równanie parametryczne:
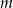 równoległej do prostej
równoległej do prostej 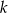 , przechodzącej przez punkt
, przechodzącej przez punkt 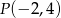 .
.  prostopadłej do prostej
prostopadłej do prostej 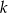 , przechodzącej przez punkt
, przechodzącej przez punkt 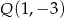 .
.Różnica współczynników kierunkowych dwóch prostych jest równa różnicy odwrotności tych współczynników. Uzasadnij, że te proste są prostopadłe albo równoległe.
Dwie proste mają tę własności, że różnica współczynnika kierunkowego i jego odwrotności w przypadku każdej z tych prostych jest taka sama. Uzasadnij, że te proste są prostopadłe albo równoległe.
Dla jakich wartości parametru 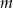 proste
proste 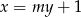 oraz
oraz 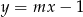 przecinają się w jednym punkcie, który leży poniżej prostej
przecinają się w jednym punkcie, który leży poniżej prostej 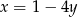 ?
?
Prosta 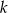 jest wykresem funkcji
jest wykresem funkcji 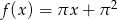 .
.
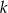 z wykresem funkcji
z wykresem funkcji 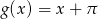 .
. 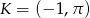 i równoległej do prostej
i równoległej do prostej 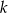 .
.Wyznacz równanie prostej równoległej do prostej 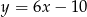 przechodzącej przez punkt
przechodzącej przez punkt 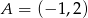 oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt
oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt 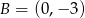 .
.
Napisz równanie prostej równoległej do prostej o równaniu 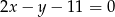 i przechodzącej przez punkt
i przechodzącej przez punkt 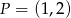 .
.
Punkt 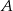 jest punktem wspólnym prostych prostopadłych
jest punktem wspólnym prostych prostopadłych 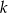 i
i 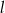 o równaniach
o równaniach 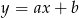 oraz
oraz 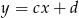 . Wykaż, że jeżeli
. Wykaż, że jeżeli 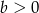 i
i 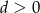 , to druga współrzędna punktu
, to druga współrzędna punktu 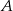 jest liczbą dodatnią.
jest liczbą dodatnią.
Określ wzajemne położenie prostych 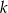 i
i 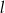 o równaniach
o równaniach
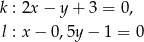
Oblicz miarę kąta ostrego, którego ramiona są zawarte w prostych o równaniach 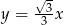 i
i 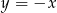 .
.
Oblicz miarę kąta ostrego, którego ramiona są zawarte w prostych o równaniach 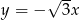 i
i 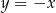 .
.
Określ wzajemne położenie prostych 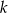 i
i 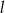 o równaniach
o równaniach
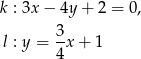
Wykaż, że cosinus kąta przecięcia się wykresów funkcji 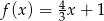 i
i 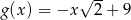 jest równy
jest równy 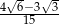 .
.
Zapisz równanie prostej przechodzącej przez punkt 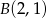 i prostopadłej do prostej danej równaniem
i prostopadłej do prostej danej równaniem 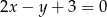 .
.
Wyznacz równanie prostej prostopadłej do prostej 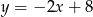 przechodzącej przez punkt
przechodzącej przez punkt 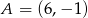 .
.
Zapisz równanie prostej przechodzącej przez punkt 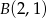 i prostopadłej do prostej danej równaniem
i prostopadłej do prostej danej równaniem 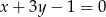 .
.
Wyznacz równanie prostej prostopadłej do prostej o równaniu 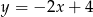 przecinającej oś
przecinającej oś 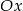 w punkcie o odciętej 4.
w punkcie o odciętej 4.
Wyznacz równanie prostej prostopadłej do prostej o równaniu 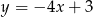 przechodzącej przez punkt
przechodzącej przez punkt 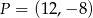 .
.
Sprawdź czy proste  i
i 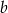 są równoległe, jeśli prosta
są równoległe, jeśli prosta  przecina oś
przecina oś  w punkcie
w punkcie 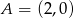 , oś
, oś 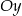 w punkcie
w punkcie 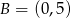 , a prosta
, a prosta 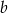 przecina oś
przecina oś 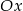 w punkcie
w punkcie 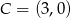 i oś
i oś 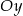 w punkcie
w punkcie 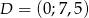 .
.
Proste o równaniach 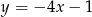 i
i 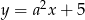 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Proste o równaniach 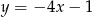 i
i 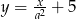 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Proste o równaniach 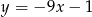 i
i 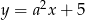 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Dane są proste o równaniach 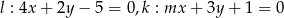 . Wyznacz parametr
. Wyznacz parametr 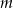 , tak aby te proste były prostopadłe.
, tak aby te proste były prostopadłe.
Dana jest funkcja 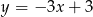 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt
. Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 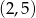 . Wykonaj rysunek do zadania.
. Wykonaj rysunek do zadania.
Dana jest funkcja 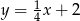 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt
. Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 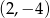 . Wykonaj rysunek do zadania.
. Wykonaj rysunek do zadania.
Prosta 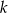 przechodzi przez punkty
przechodzi przez punkty 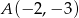 i
i 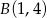 . Wyznacz równania prostej
. Wyznacz równania prostej 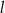 prostopadłej do
prostopadłej do 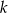 i prostej
i prostej 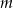 równoległej do
równoległej do 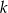 , jeżeli każda z nich przechodzi przez punkt
, jeżeli każda z nich przechodzi przez punkt 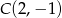 .
.
Określ wzajemne położenie prostych