Prostokątną działkę o powierzchni 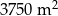 podzielono na trzy prostokątne działki o jednakowych wymiarach, w sposób przedstawiony na rysunku.
podzielono na trzy prostokątne działki o jednakowych wymiarach, w sposób przedstawiony na rysunku.

Jakie wymiary miała działka przed podziałem?
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Prostokątną działkę o powierzchni 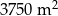 podzielono na trzy prostokątne działki o jednakowych wymiarach, w sposób przedstawiony na rysunku.
podzielono na trzy prostokątne działki o jednakowych wymiarach, w sposób przedstawiony na rysunku.

Jakie wymiary miała działka przed podziałem?
Prostokątną działkę o powierzchni 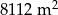 podzielono na pięć prostokątnych działek o jednakowych wymiarach i dwie działki w kształcie kwadratu (zobacz rysunek).
podzielono na pięć prostokątnych działek o jednakowych wymiarach i dwie działki w kształcie kwadratu (zobacz rysunek).
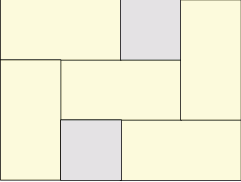
Jakie wymiary miała działka przed podziałem?
Prostokątny arkusz blachy o powierzchni 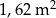 pocięto na przystające prostokąty, w sposób przedstawiony na rysunku.
pocięto na przystające prostokąty, w sposób przedstawiony na rysunku.

Jakie wymiary miał ten arkusz blachy przed pocięciem?
Poparcie społeczne dla partii „Zielone żabki” w marcu było równe 25%, a w kwietniu 20%. Zatem poparcie w kwietniu zmalało w porównaniu z marcem o:
A) 5% B) 15% C) 20% D) 25%
Poparcie dla partii "WESELI" w marcu było równe 24%. W kwietniu poparcie dla tej partii wynosiło 30%. Zatem poparcie dla partii "WESELI" wzrosło o
A) 3% B) 12,5% C) 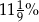 D) 25%
D) 25%
Poparcie dla partii "WESELI" w marcu było równe 40%. W kwietniu poparcie dla tej partii wynosiło 34%. Zatem poparcie dla partii "WESELI" zmalało o
A) 6% B) 12,5% C) 15% D) 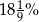
Poparcie społeczne dla partii „Radość i słońce” w marcu było równe 15%, a w kwietniu 12%. Zatem poparcie w kwietniu zmalało w porównaniu z marcem o:
A) 20% B) 6% C) 3% D) 25%
Poparcie społeczne dla partii „Radosna przyszłość” w marcu było równe 20%, a w kwietniu 15%. Zatem poparcie w kwietniu zmalało w porównaniu z marcem o:
A) 5% B) 15% C) 20% D) 25%
Poparcie dla partii "WESELI" w marcu było równe 24%. W kwietniu poparcie dla tej partii wynosiło 27%. Zatem poparcie dla partii "WESELI" wzrosło o
A) 3% B) 12,5% C) 25% D) 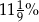
Przedstawiony na rysunku trójkąt 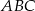 jest prostokątny, ale nie jest równoramienny. Odcinek
jest prostokątny, ale nie jest równoramienny. Odcinek 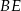 jest wysokością w trójkącie
jest wysokością w trójkącie 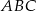 , a półprosta
, a półprosta 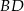 jest dwusieczną kąta prostego.
jest dwusieczną kąta prostego.
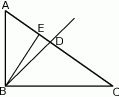
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
Półprosta 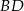 jest dwusieczną kąta jest dwusieczną kąta 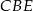 . . | P | F |
Odcinek 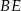 jest wysokością w trójkącie jest wysokością w trójkącie 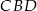 . . | P | F |
Punkt 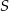 jest środkiem okręgu wpisanego w trójkąt równoramienny
jest środkiem okręgu wpisanego w trójkąt równoramienny 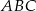 (
(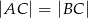 ).
).
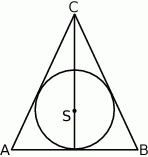
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
Prosta 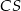 zawiera środkową trójkąta zawiera środkową trójkąta 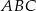 . . | P | F |
Prosta 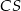 jest symetralną odcinka jest symetralną odcinka 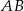 | P | F |
Z okazji Światowego Dnia Książki uczniowie klasy VII zorganizowali quiz wiedzy o postaciach literackich. Quiz można było zakończyć na jednym z poziomów, które zaliczało się kolejno od I do VI. Na diagramie przedstawiono, ile procent uczniów zakończyło quiz na danym poziomie. Na poziomach niższych niż Asia quiz zakończyło dokładnie 32% uczniów biorących w nim udział.
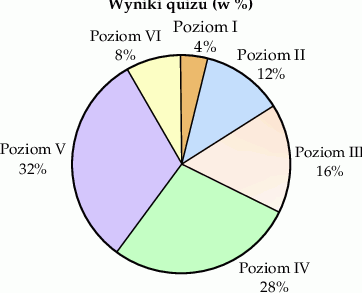
Ile procent uczniów zakończyło ten quiz na poziomach wyższych niż Asia?
A) 40% B) 32% C) 28% D) 8%
Z okazji Międzynarodowego Dnia Liczby 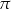 zorganizowano konkurs matematyczny w jednej ze szkół podstawowych. Każdy z uczestników konkursu zajmował jedno z miejsc numerowanych kolejno od I do VI. Na diagramie przedstawiono, ile procent uczniów zakończyło konkurs na danym miejscu. Wiadomo, że 49% uczniów zajęło miejsce o numerze wyższym niż Amelia.
zorganizowano konkurs matematyczny w jednej ze szkół podstawowych. Każdy z uczestników konkursu zajmował jedno z miejsc numerowanych kolejno od I do VI. Na diagramie przedstawiono, ile procent uczniów zakończyło konkurs na danym miejscu. Wiadomo, że 49% uczniów zajęło miejsce o numerze wyższym niż Amelia.
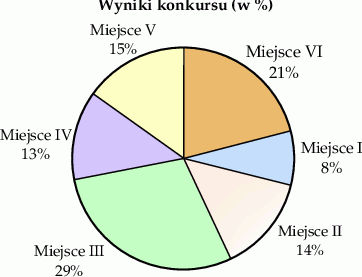
Ile procent uczniów zakończyło konkurs na miejscach o numerach niższych niż Amelia?
A) 8% B) 22% C) 51% D) 36%
Jakie stężenie ma roztwór cukru w wodzie, jeśli sporządziliśmy go z 3g cukru i 57g wody?
Dany jest trójkąt prostokątny. Wykaż, że suma pól kół o średnicach będących przyprostokątnymi trójkąta jest równa polu koła o średnicy równej przeciwprostokątnej.
Na bokach trójkąta prostokątnego zbudowano trójkąty równoboczne. Wykaż, że pole figury zbudowanej na przeciwprostokątnej jest równe sumie pól figur zbudowanych na przyprostokątnych.
Do księgarni językowej dostarczono łącznie 240 książek napisanych w czterech różnych językach. Książek w języku włoskim było 3 razy mniej niż książek w języku niemieckim, książek w języku angielskim było 2 razy więcej niż w języku niemieckim, a książek w języku francuskim było o 20 więcej niż w języku włoskim. Oblicz, ile książek napisanych w języku francuskim dostarczono do tej księgarni.
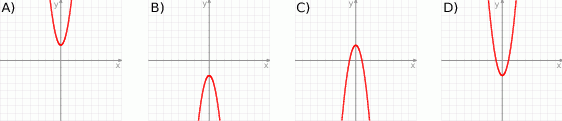
Na którym rysunku przedstawiono wykres funkcji 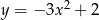 ?
?
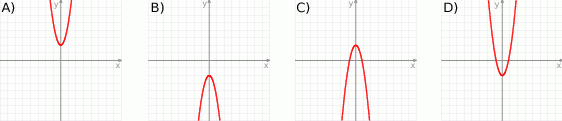
Na którym rysunku przedstawiono wykres funkcji 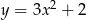 ?
?
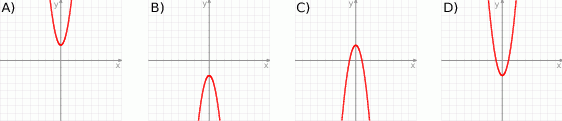
Na którym rysunku przedstawiono wykres funkcji 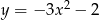 ?
?
Jeden bok kwadratu o polu 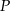 zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
A) 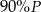 B)
B) 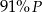 C)
C) 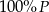 D)
D) 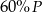
Jeden bok kwadratu wydłużono o 10%, a drugi bok skrócono o 10% w taki sposób, że otrzymano prostokąt. Pole tego prostokąta jest
A) równe polu kwadratu
B) mniejsze od pola kwadratu o 10%
C) większe od pola kwadratu o 10%
D) mniejsze od pola kwadratu o 1%
Dane są liczby  i
i 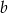 takie, że
takie, że 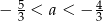 oraz
oraz 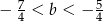 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloraz 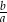 jest zawsze dodatni. jest zawsze dodatni. | P | F |
Różnica 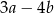 jest zawsze dodatnia. jest zawsze dodatnia. | P | F |
Odległość między orbitami Saturna i Ziemi jest równa 1277 mln km.Czy sonda kosmiczna pokonująca w ciągu dnia 1,5 mln km przebędzie tę odległość w ciągu roku? Oszacuj wyniki, nie wykonując dokładnych rachunków.
Staropolska mila była równa 7146 m i dzieliła się na 8 stajań. W XIX wieku wprowadzono nowopolską milę równą 8534,3 m i dzielącą się na 8 wiorst. Czy kilometr jest jednostką większą czy mniejszą od stajania i wiorsty? Oszacuj wyniki, nie wykonując dokładnych rachunków.
Właściciel sklepu kupił w hurtowni 30 książek i 20 poradników za 1020 zł. Poradniki sprzedał z zyskiem 20%, a książki z zyskiem 25%. W ten sposób zarobił 240 zł. Oblicz, w jakiej cenie sklepikarz kupił w hurtowni książki, a w jakiej poradniki.
Marcin zarabiał miesięcznie 3400 zł, a Adam 4300 zł. Obaj otrzymali w swoich firmach podwyżki. Podwyżka otrzymana przez Adama była o 4 punkty procentowe niższa niż podwyżka otrzymana przez Marcina. Po podwyżce obaj panowie zarabiają łącznie 8452 zł. Ile zarabia każdy z panów po podwyżce? Zapisz wszystkie obliczenia.
Karol zarabiał miesięcznie 4200 zł, a Jan 3800 zł. Obaj otrzymali w swoich firmach podwyżki. Podwyżka otrzymana przez Jana była o 3 punkty procentowe wyższa niż podwyżka otrzymana przez Karola. Po podwyżce obaj panowie zarabiają łącznie 9074 zł. Ile zarabia każdy z panów po podwyżce? Zapisz wszystkie obliczenia.
Ojciec i córka mają razem 50 lat. Pięć lat temu ojciec był 9 razy starszy od córki. Ile lat ma obecnie każde z nich.
Matka i córka mają łącznie 60 lat, a 10 lat temu matka był czterokrotnie starsza od córki. Ile lat ma matka, a ile córka?
Matka i córka mają łącznie 68 lat, a 8 lat temu matka był trzykrotnie starsza od córki. Ile lat ma matka, a ile córka?
Ojciec i syn mają łącznie 52 lata. Sześć lat temu ojciec był trzykrotnie starszy od syna. Ile lat ma ojciec, a ile syn?
Basia jest o 8 lat młodsza od Kasi. Za 30 lat będą miały razem 116 lat. Ile lat ma każda z nich obecnie?
Ojciec i syn mają łącznie 50 lat. Pięć lat temu ojciec był trzykrotnie starszy od syna. Ile lat ma ojciec, a ile syn?
Janek jest o 6 lat młodszy od Michała. Za 30 lat będą mieli razem 104 lata. Ile lat ma każdy z nich obecnie?
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego wierzchołków jest punkt 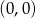 , a jeden z jego boków leży na osi
, a jeden z jego boków leży na osi  . Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi
. Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi  . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
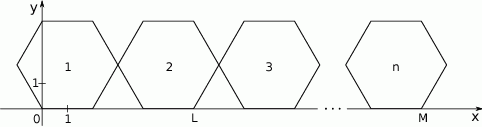
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwsza współrzędna wierzchołka 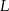 w drugim sześciokącie jest równa 6. w drugim sześciokącie jest równa 6. | P | F |
Pierwsza współrzędna wierzchołka 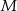 w w  –tym sześciokącie jest równa –tym sześciokącie jest równa 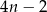 . . | P | F |
W układzie współrzędnych narysowano kwadrat o przekątnej długości 4 tak, że jednym z jego wierzchołków jest punkt 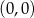 , a jedna z jego przekątnych jest równoległa do osi
, a jedna z jego przekątnych jest równoległa do osi 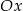 . Do tego kwadratu dorysowujemy kolejne takie same kwadraty. Umieszczamy je tak, jak na rysunku, aby każdy następny kwadrat miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jedna z przekątnych każdego kwadratu była równoległa do osi
. Do tego kwadratu dorysowujemy kolejne takie same kwadraty. Umieszczamy je tak, jak na rysunku, aby każdy następny kwadrat miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jedna z przekątnych każdego kwadratu była równoległa do osi 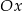 . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, kwadraty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, kwadraty, które ponumerowano kolejnymi liczbami naturalnymi.
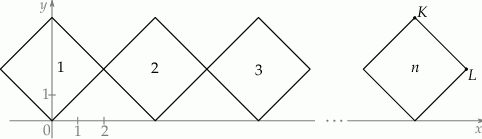
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwsza współrzędna wierzchołka 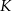 w w  –tym kwadracie jest równa –tym kwadracie jest równa 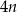 . . | P | F |
Pierwsza współrzędna wierzchołka 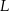 w w  –tym kwadracie jest równa –tym kwadracie jest równa 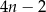 . . | P | F |
W układzie współrzędnych narysowano trójkąt równoboczny tak, że jednym z jego wierzchołków jest punkt 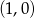 , jeden z wierzchołków jest na osi
, jeden z wierzchołków jest na osi 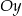 , a jeden z jego boków jest równoległy do osi
, a jeden z jego boków jest równoległy do osi 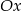 . Do tego trójkąta dorysowujemy kolejne takie same trójkąty. Umieszczamy je tak, jak na rysunku, aby każdy następny trójkąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego trójkąta był równoległy do osi
. Do tego trójkąta dorysowujemy kolejne takie same trójkąty. Umieszczamy je tak, jak na rysunku, aby każdy następny trójkąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego trójkąta był równoległy do osi  . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, trójkąty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, trójkąty, które ponumerowano kolejnymi liczbami naturalnymi.
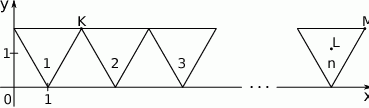
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek 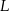 w w  –tym trójkącie ma współrzędne –tym trójkącie ma współrzędne 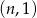 . . | P | F |
Wierzchołek 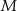 w w  –tym trójkącie ma współrzędne –tym trójkącie ma współrzędne 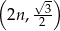 . . | P | F |
O liczbie  wiemy, że
wiemy, że 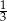 tej liczby jest o
tej liczby jest o  większa od
większa od  tej liczby. Które równanie pozwoli wyznaczyć liczbę
tej liczby. Które równanie pozwoli wyznaczyć liczbę  ?
?
A) 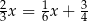 B)
B) 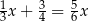 C)
C) 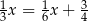 D)
D) 
O liczbie  wiemy, że
wiemy, że 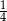 tej liczby jest o
tej liczby jest o  mniejsza od
mniejsza od 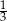 tej liczby. Które równanie pozwoli wyznaczyć liczbę
tej liczby. Które równanie pozwoli wyznaczyć liczbę  ?
?
A) 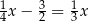 B)
B) 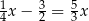 C)
C) 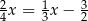 D)
D) 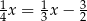
Która z poniższych liczb jest większa od 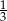 ?
?
A) 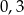 B)
B) 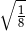 C)
C) 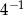 D)
D) 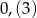
Która z poniższych liczb jest większa od  ?
?
A) 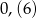 B)
B) 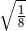 C)
C) 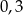 D)
D) 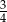
Która z poniższych liczb jest większa od 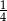 ?
?
A) 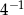 B)
B) 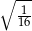 C)
C) 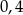 D)
D) 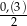
Roczne oprocentowanie lokaty, które wynosiło 6%, zmniejszono o 25%. Oblicz, o ile punktów procentowych zmniejszono to oprocentowanie.
Roczne oprocentowanie lokaty, które wynosiło 8%, zmniejszono o 37,5%. Oblicz, o ile punktów procentowych zmniejszono to oprocentowanie.
Adam zapisał, w przypadkowej kolejności, podane w programie radiowym wartości temperatury odnotowane pewnego zimowego dnia o godzinie 20:30 w Zakopanem, w Wiśle, w Karpaczu i w Szklarskiej Porębie (zobacz rysunek).
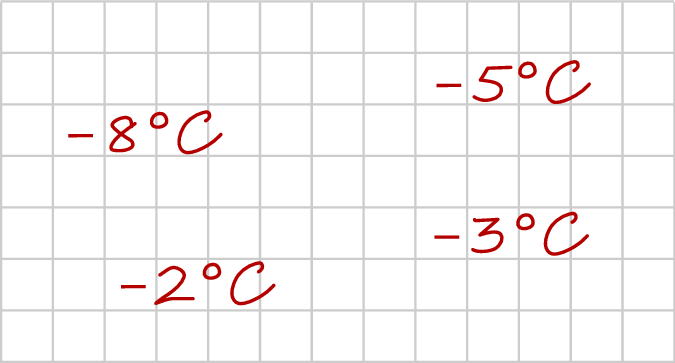
Temperatura w Karpaczu była o 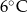 wyższa niż w Szklarskiej Porębie, a w Wiśle była niższa niż w Zakopanem. Temperaturę
wyższa niż w Szklarskiej Porębie, a w Wiśle była niższa niż w Zakopanem. Temperaturę 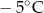 zanotowano w
zanotowano w
A) Szklarskiej Porębie. B) Zakopanem. C) Karpaczu. D) Wiśle.
Rozwiązaniem układu równań 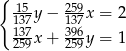 jest para liczb
jest para liczb
A) 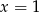 i
i 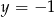 B)
B) 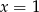 i
i 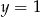 C)
C) 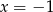 i
i 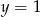 D)
D) 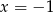 i
i 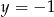
Na rysunku przedstawiono czworokąt 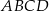 , w którym
, w którym 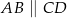 i trójkąt równoramienny
i trójkąt równoramienny 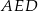 , w którym
, w którym 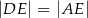 . Miara kąta
. Miara kąta 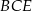 jest równa
jest równa 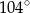 , a miara kąta
, a miara kąta 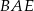 jest równa
jest równa 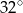 .
.
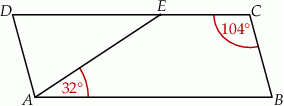
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 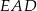 ma miarę ma miarę 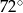 . . | P | F |
Czworokąt 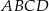 jest równoległobokiem. jest równoległobokiem. | P | F |
