Dany jest ciąg 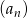 określony dla każdej liczby całkowitej
określony dla każdej liczby całkowitej 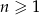 , w którym dla każdej liczby
, w którym dla każdej liczby 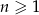 prawdziwe są równości
prawdziwe są równości
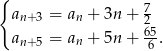
Wykaż, że ciąg 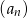 jest ciągiem rosnącym.
jest ciągiem rosnącym.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest ciąg 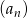 określony dla każdej liczby całkowitej
określony dla każdej liczby całkowitej 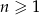 , w którym dla każdej liczby
, w którym dla każdej liczby 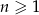 prawdziwe są równości
prawdziwe są równości
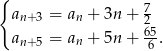
Wykaż, że ciąg 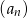 jest ciągiem rosnącym.
jest ciągiem rosnącym.
Ciąg 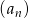 określony jest rekurencyjnie:
określony jest rekurencyjnie: 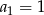 ,
, 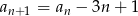 dla
dla 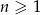 .
.
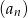 .
. 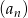 .
.Dany jest ciąg 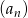 określony dla każdej liczby całkowitej
określony dla każdej liczby całkowitej 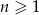 , w którym
, w którym 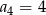 oraz dla każdej liczby
oraz dla każdej liczby 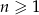 prawdziwa jest równość
prawdziwa jest równość 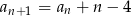 . Oblicz pierwszy wyraz ciągu
. Oblicz pierwszy wyraz ciągu 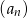 i ustal, czy ciąg ten jest malejący.
i ustal, czy ciąg ten jest malejący.
Ciąg 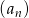 określony jest rekurencyjnie:
określony jest rekurencyjnie: 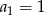 ,
, 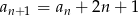 dla
dla 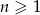 .
.
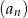 .
. 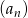 .
.Dany jest ciąg 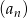 określony dla każdej liczby całkowitej
określony dla każdej liczby całkowitej 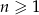 , w którym
, w którym 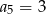 oraz dla każdej liczby
oraz dla każdej liczby 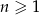 prawdziwa jest równość
prawdziwa jest równość 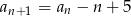 . Oblicz pierwszy wyraz ciągu
. Oblicz pierwszy wyraz ciągu 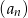 i ustal, czy ciąg ten jest rosnący.
i ustal, czy ciąg ten jest rosnący.
Podaj wzór na  -ty wyraz ciągu
-ty wyraz ciągu 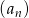 , jeżeli
, jeżeli 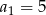 i
i 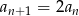 dla
dla 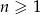 .
.
Oblicz sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 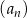 określonego dla
określonego dla 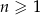 , w którym
, w którym
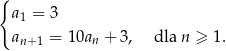
Określono ciąg wzorem rekurencyjnym: 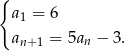 Jaką wartość ma 5 wyraz tego ciągu?
Jaką wartość ma 5 wyraz tego ciągu?
Określono ciąg wzorem rekurencyjnym: 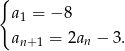 Jaką wartość ma 5 wyraz tego ciągu?
Jaką wartość ma 5 wyraz tego ciągu?
Oblicz sumę 50 początkowych wyrazów ciągu 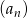 , który określony jest w następujący sposób
, który określony jest w następujący sposób
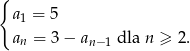
Ciąg 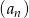 określony dla
określony dla 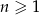 jest rosnący, ma wszystkie wyrazy ujemne oraz spełnia warunki
jest rosnący, ma wszystkie wyrazy ujemne oraz spełnia warunki
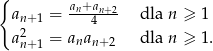
Oblicz iloraz 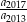 .
.
Dany jest ciąg określony rekurencyjnie
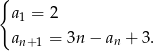
Wyznacz liczby całkowite 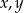 tak, aby ciąg
tak, aby ciąg 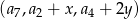 był ciągiem arytmetycznym, natomiast ciąg
był ciągiem arytmetycznym, natomiast ciąg 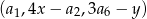 był ciągiem geometrycznym.
był ciągiem geometrycznym.
Ciąg 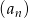 , gdzie
, gdzie 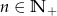 , określony jest następująco:
, określony jest następująco:
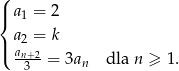
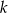 , jeżeli ciąg
, jeżeli ciąg 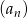 jest ciągiem geometrycznym, w którym suma sześciu początkowych wyrazów jest równa
jest ciągiem geometrycznym, w którym suma sześciu początkowych wyrazów jest równa 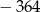 .
.  suma
suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 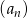 jest równa 9842.
jest równa 9842.Ciąg 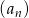 jest określony rekurencyjnie w następujący sposób
jest określony rekurencyjnie w następujący sposób
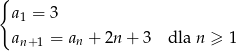
Oblicz ile wyrazów tego ciągu jest mniejszych niż 2018.
Ciąg 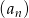 , gdzie
, gdzie 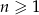 dany jest wzorem rekurencyjnym
dany jest wzorem rekurencyjnym
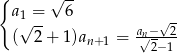
 , dla których spełniona jest nierówność
, dla których spełniona jest nierówność 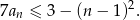
Dany jest ciąg 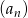 określony rekurencyjnie
określony rekurencyjnie
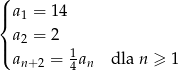
Oblicz sumę 18 początkowych wyrazów ciągu 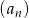 .
.
Wyznacz drugi, trzeci i czwarty wyraz ciągu określonego wzorem rekurencyjnym:
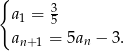
Dla wyznaczonych wyrazów znajdź taką liczbę  , aby ciąg
, aby ciąg 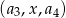 był ciągiem geometrycznym.
był ciągiem geometrycznym.
Dany jest ciąg 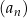 określony wzorem rekurencyjnym
określony wzorem rekurencyjnym
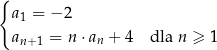
Oblicz sumę czterech początkowych wyrazów ciągu 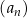 .
.
Ciąg 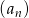 , gdzie
, gdzie 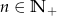 , określony jest następująco:
, określony jest następująco:
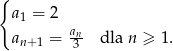
Wyznacz wszystkie wartości 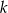 , dla których suma
, dla których suma 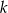 początkowych wyrazów ciągu
początkowych wyrazów ciągu 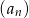 jest większa od
jest większa od 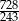 .
.
Ciąg 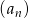 , gdzie
, gdzie 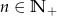 , określony jest następująco:
, określony jest następująco:
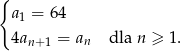
Wyznacz wszystkie wartości 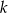 , dla których suma
, dla których suma 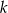 początkowych wyrazów ciągu
początkowych wyrazów ciągu 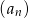 jest równa
jest równa 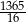 .
.
Ciąg 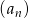 jest określony wzorem
jest określony wzorem
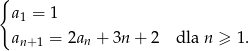
Oblicz średnią arytmetyczną liczb 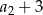 i
i 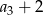 .
.
Określ wzorem rekurencyjnym ciąg którego pierwszy i drugi wyraz jest równy 3, a każdy następny jest iloczynem dwóch poprzednich.
Ciągiem Fibonacciego nazywamy ciąg, którego dwa pierwsze wyrazy są równe 1, a każdy kolejny jest sumą dwóch poprzednich. Jaką liczbą, parzystą czy nieparzystą, jest 528 wyraz ciągu Fibonacciego? Odpowiedź uzasadnij.
