Dany przez sumy wyrazów - zadania z matematyki

/Szkoła średnia/Ciągi/Geometryczny/Dany przez sumy wyrazów

Wyznacz wszystkie ciągi geometryczne o wyrazach różnych od zera, w których każdy wyraz, rozpoczynając od wyrazu trzeciego, jest równy średniej arytmetycznej dwóch poprzednich wyrazów.

Iloraz ciągu geometrycznego 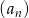(an) równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18.

Oblicz pierwszy wyraz ciągu .
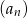Podaj wzór na wyraz ogólny ciągu .

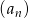Suma 2018 początkowych wyrazów ciągu geometrycznego 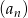(an ) jest równa 1417, a suma odwrotności tych wyrazów jest równa 109. Oblicz iloczyn 2018 początkowych wyrazów ciągu (an) .

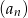Wyrazy ciągu geometrycznego 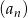(an) , określonego dla 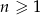n ≥ 1 , spełniają układ równań

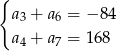
{ a3 + a6 = − 84 a + a = 168 4 7

Wyznacz liczbę początkowych wyrazów tego ciągu, których suma 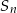jest równa 32769.

Ukryj Podobne zadania

Wyrazy ciągu geometrycznego 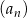(an) , określonego dla 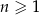n ≥ 1 , spełniają układ równań

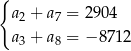
{ a2 + a7 = 2 904 a + a = − 8 712 3 8

Wyznacz liczbę początkowych wyrazów tego ciągu, których suma 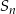jest równa 177148.

W ciągu geometrycznym 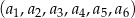(a1,a2,a3,a4,a5,a6) suma wyrazów o numerach nieparzystych jest równa 182, a stosunek sumy wyrazów o numerach nieparzystych do sumy wyrazów o numerach parzystych jest równy 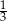. Wyznacz wszystkie wyrazy tego ciągu.

W ciągu geometrycznym 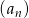(an) , określonym dla 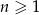n ≥ 1 , dane są: wyraz 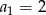a1 = 2 i suma trzech początkowych wyrazów tego ciągu 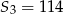S3 = 11 4 . Wiadomo ponadto, że 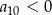a10 < 0 . Oblicz iloraz

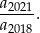
a -2021. a2018

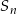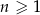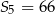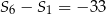W ciągu geometrycznym przez oznaczamy sumę początkowych wyrazów tego ciągu, dla liczb naturalnych n ≥ 1 . Wiadomo, że dla pewnego ciągu geometrycznego: S5 = 66 i S6 − S1 = − 33 . Wyznacz iloraz i ósmy wyraz tego ciągu.

W skończonym ciągu geometrycznym 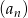(an ) wyraz pierwszy jest równy 3, a wyraz ostatni 768. Wiedząc, że suma wszystkich wyrazów wynosi 1533, oblicz iloraz tego ciągu.

Ukryj Podobne zadania

W skończonym ciągu geometrycznym 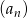(an ) wyraz pierwszy jest równy 2, a wyraz ostatni 39 366. Wiedząc, że suma wszystkich wyrazów wynosi 59 048, oblicz iloraz tego ciągu.

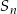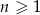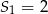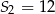W ciągu geometrycznym przez oznaczamy sumę początkowych wyrazów tego ciągu, dla liczb naturalnych n ≥ 1 . Wiadomo, że dla pewnego ciągu geometrycznego: S1 = 2 i S2 = 12 . Wyznacz iloraz i piąty wyraz tego ciągu.

Ukryj Podobne zadania

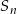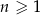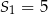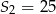W ciągu geometrycznym przez oznaczamy sumę początkowych wyrazów tego ciągu, dla liczb naturalnych n ≥ 1 . Wiadomo, że dla pewnego ciągu geometrycznego: S1 = 5 i S2 = 25 . Wyznacz iloraz i szósty wyraz tego ciągu.

Ciąg geometryczny 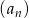(an ) ma 100 wyrazów i są one liczbami dodatnimi. Suma wszystkich wyrazów o numerach nieparzystych jest sto razy większa od sumy wszystkich wyrazów o numerach parzystych oraz

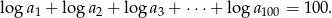
log a1 + lo ga2 + log a3 + ⋅ ⋅⋅+ log a100 = 100.

Oblicz .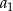

W ciągu geometrycznym 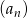(an) dane są iloraz 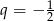1 q = − 2 oraz suma

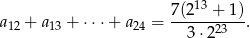
13 a12 + a13 + ⋅⋅⋅ + a24 = 7(2--+-1) . 3 ⋅223

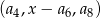Oblicz , dla którego ciąg (a4,x − a6,a8) jest ciągiem arytmetycznym.

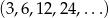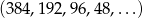Dane są dwa skończone ciągi geometryczne (3,6,12,24 ,...) i (384,1 92,96,48,...) o tej samej liczbie wyrazów. Znajdź liczbę wyrazów każdego z tych ciągów wiedząc, że łączna suma ich wyrazów wynosi 1530.

W ciągu geometrycznym 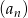(an) dane są iloraz 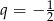1 q = − 2 oraz suma

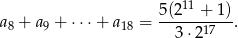
11 a8 + a9 + ⋅ ⋅⋅+ a18 = 5-(2-+-1) . 3⋅217

Oblicz .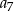

Suma ośmiu początkowych wyrazów ciągu geometrycznego 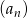(an) , określonego dla 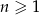n ≥ 1 , jest równa 55760. Ponadto 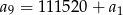a9 = 1115 20+ a1 . Oblicz iloraz tego ciągu.

Iloraz ciągu geometrycznego 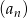(an) jest równy 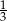1 3 , a suma jego pięciu początkowych wyrazów wynosi 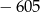− 60 5 . Znajdź pierwszy wyraz ciągu 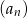(an ) oraz określ jego monotoniczność.

Wyznacz iloraz niezerowego ciągu geometrycznego, w którym suma 10 początkowych wyrazów jest 5 razy większa od sumy pierwszych 5 wyrazów.

W ciągu geometrycznym 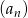(an) , którego żaden wyraz nie jest równy 0, suma pewnych dwóch kolejnych wyrazów jest równa 0. Oblicz sumę 2008 początkowych wyrazów tego ciągu.

Iloraz ciągu geometrycznego 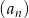(an) , gdzie 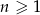n ≥ 1 jest równy 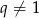q ⁄= 1 , a suma 10 początkowych wyrazów tego ciągu spełnia warunek 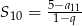S10 = 5−1a−q11 . Oblicz pierwszy wyraz tego ciągu.

Liczby 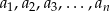a1,a2,a3,...,an są kolejnymi wyrazami ciągu geometrycznego o dodatnich wyrazach, a jest liczbą parzystą. Znając sumy

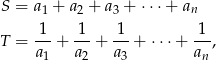
S = a1 + a2 + a 3 + ⋅⋅⋅ + an 1-- -1- 1-- 1-- T = a + a + a + ⋅⋅⋅+ a , 1 2 3 n

oblicz iloczyn 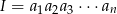I = a a a ⋅⋅⋅a 1 2 3 n .

Siódmy wyraz ciągu geometrycznego 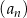(an) , określonego dla 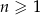n ≥ 1 , jest równy 6, a suma jego sześciu początkowych wyrazów jest równa 756. Iloraz 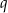tego ciągu spełnia warunek: 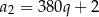a2 = 3 80q+ 2 . Oblicz pierwszy wyraz oraz iloraz tego ciągu.

Strona 1 z 2