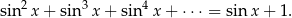Rozwiąż układ równań 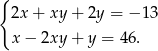
/Szkoła średnia/Równania
Wyznacz wszystkie wartości parametru 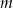 , dla których równanie
, dla których równanie
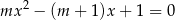
ma dwa różne rozwiązania rzeczywiste 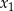 oraz
oraz 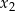 , spełniające warunek:
, spełniające warunek:
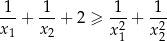
Wyznacz wszystkie wartości parametru 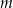 , dla których równanie
, dla których równanie
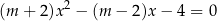
ma dwa różne rozwiązania rzeczywiste 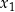 oraz
oraz 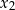 , spełniające warunek:
, spełniające warunek:
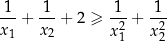
Wyznacz wszystkie wartości parametru 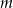 , dla których równanie
, dla których równanie 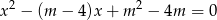 ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od
ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od 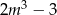 .
.
Rozwiąż układ równań 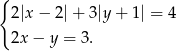
Rozwiąż równanie 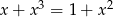 .
.
Rozwiąż równanie 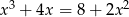 .
.
Rozwiąż równanie
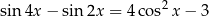
w zbiorze ![[0,2π ]](https://img.zadania.info/zad/1452081/HzadT1x.png) .
.
Wyznacz współczynniki 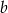 i
i  trójmianu kwadratowego
trójmianu kwadratowego 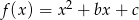 , wiedząc że jego miejsca zerowe
, wiedząc że jego miejsca zerowe 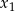 i
i 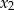 spełniają warunek:
spełniają warunek: 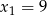 i
i 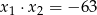 .
.
Rozwiąż algebraicznie układ równań 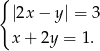
Wykaż, że równanie 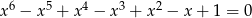 nie ma rozwiązań rzeczywistych.
nie ma rozwiązań rzeczywistych.
Rozwiąż równanie 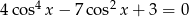 .
.
Rozwiąż równanie 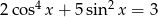 w przedziale
w przedziale 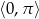 .
.
Rozwiąż graficznie i algebraicznie układ równań
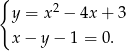
Dane jest równanie 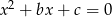 z niewiadomą
z niewiadomą  . Wyznacz wartości
. Wyznacz wartości 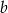 i
i  tak, by były one rozwiązaniami danego równania.
tak, by były one rozwiązaniami danego równania.
W prostokątnym układzie współrzędnych zaznacz zbiór wszystkich punktów płaszczyzny, których współrzędne spełniają warunek 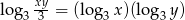 .
.
W prostokątnym układzie współrzędnych zaznacz zbiór wszystkich punktów płaszczyzny, których współrzędne spełniają warunek 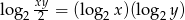 .
.
Różnymi pierwiastkami równania kwadratowego 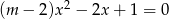 są liczby
są liczby 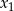 oraz
oraz 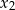 . Narysuj wykres funkcji
. Narysuj wykres funkcji 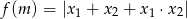 .
.
Dla jakich wartości parametru 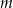 równanie
równanie 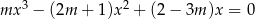 ma rozwiązania, których suma jest dodatnia?
ma rozwiązania, których suma jest dodatnia?
Wyznacz miarę kąta ostrego  , dla którego wyrażenie
, dla którego wyrażenie 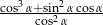 ma wartość 2.
ma wartość 2.
Wyznacz miarę kąta ostrego  , dla którego wyrażenie
, dla którego wyrażenie 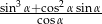 przyjmuje wartość
przyjmuje wartość 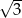 .
.
Wyznacz te wartości parametru 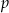 , dla których równanie
, dla których równanie 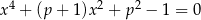 ma dokładnie dwa różne pierwiastki.
ma dokładnie dwa różne pierwiastki.
Wyznacz te wartości parametru 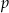 , dla których równanie
, dla których równanie 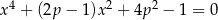 ma dokładnie dwa różne pierwiastki rzeczywiste.
ma dokładnie dwa różne pierwiastki rzeczywiste.
Dla jakich wartości parametru 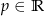 równanie
równanie 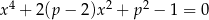 ma dokładnie dwa różne rozwiązania?
ma dokładnie dwa różne rozwiązania?
Wyznacz te wartości parametru 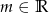 , dla których równanie
, dla których równanie
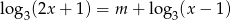
ma pierwiastek należący do zbioru 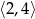 .
.
Dla jakich wartości parametru 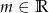 pierwiastek równania
pierwiastek równania 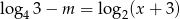 należy do przedziału
należy do przedziału 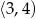 ?
?
Rozwiąż równanie 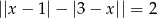 .
.
Rozwiąż równanie 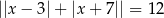 .
.
Rozwiąż równanie 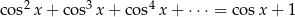
Wyznacz wszystkie liczby rzeczywiste 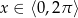 , które spełniają równanie
, które spełniają równanie