Podstawa 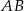 trójkąta równoramiennego
trójkąta równoramiennego 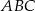 ma długość 4, a ramiona mają długość 8.
ma długość 4, a ramiona mają długość 8.
- Oblicz długość promienia okręgu wpisanego w ten trójkąt.
- Oblicz dlugość promienia okręgu opisanego na tym trójkącie.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Podstawa 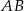 trójkąta równoramiennego
trójkąta równoramiennego 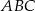 ma długość 4, a ramiona mają długość 8.
ma długość 4, a ramiona mają długość 8.
W trójkącie  dane są długości boków
dane są długości boków 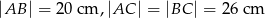 . Wyznacz długość środkowej
. Wyznacz długość środkowej 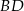 .
.
Udowodnij, że w trójkącie równoramiennym wysokości poprowadzone do równych boków są równej długości.
W trójkąt równoramienny  o podstawie długości
o podstawie długości 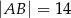 i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek
i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek 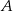 z punktem wspólnym okręgu i ramienia
z punktem wspólnym okręgu i ramienia 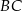 .
.
W okrąg o promieniu 13 wpisano rozwartokątny trójkąt równoramienny o podstawie 10. Oblicz pole tego trójkąta.
Dany jest trójkąt równoramienny 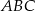 , w którym
, w którym 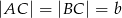 i
i 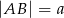 . Punkty
. Punkty 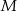 i
i 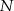 są rzutami prostopadłymi środka podstawy
są rzutami prostopadłymi środka podstawy 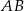 trójkąta na ramiona
trójkąta na ramiona 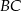 i
i 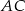 . Wyraź pole czworokąta
. Wyraź pole czworokąta 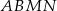 za pomocą
za pomocą  i
i 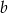 .
.
Dany jest trójkąt równoramienny 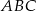 , w którym
, w którym 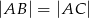 i
i 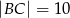 . Na boku
. Na boku 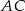 wybrano punkt
wybrano punkt 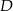 w ten sposób, że
w ten sposób, że 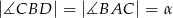 oraz
oraz 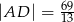 . Oblicz
. Oblicz 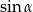 .
.
Pole trójkąta równoramiennego jest równe 25. Oblicz długość promienia okręgu wpisanego w trójkąt wiedząc, że ramię jest dwa razy dłuższe od podstawy.
Podstawa trójkąta równoramiennego ma długość 4. Środek okręgu opisanego na tym trójkącie dzieli jedną z wysokości trójkąta na odcinki, których stosunek długości wynosi 3:5. Oblicz długość ramienia trójkąta.
Ramię trójkąta równoramiennego jest dwa razy dłuższe od podstawy. Wyznacz obwód trójkąta, jeśli środkowa poprowadzona do ramienia ma długość 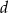 .
.
Podstawa trójkąta równoramiennego ma długość 10, a cosinus jednego z jego kątów jest równy 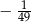 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
W trójkącie równoramiennym ramię jest 2 razy dłuższe od podstawy. Suma długości promieni okręgu wpisanego i opisanego na tym trójkącie równa się 11. Oblicz długość podstawy trójkąta.
Dany jest trójkąt równoramienny 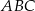 , w którym podstawa
, w którym podstawa 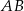 ma długość 32, a każde z ramion
ma długość 32, a każde z ramion 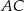 i
i 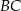 ma długość równą 34. Punkt
ma długość równą 34. Punkt 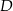 jest środkiem ramienia
jest środkiem ramienia 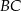 (zobacz rysunek).
(zobacz rysunek).
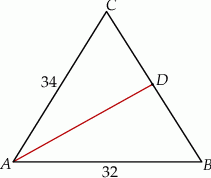
Oblicz długość odcinka 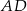 .
.
W trójkącie 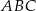 boki
boki 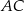 i
i 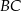 są równe. Okrąg, którego średnicą jest wysokość
są równe. Okrąg, którego średnicą jest wysokość 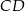 trójkąta przecina boki trójkąta w punktach dzielących te boki w stosunku 5:3 licząc od wierzchołka
trójkąta przecina boki trójkąta w punktach dzielących te boki w stosunku 5:3 licząc od wierzchołka 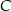 . Oblicz pole trójkąta
. Oblicz pole trójkąta 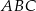 , jeżeli
, jeżeli 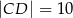 .
.
Podstawa trójkąta równoramiennego ma miarę 4 cm, a kąt przy niej 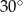 . Oblicz pole i obwód trójkąta.
. Oblicz pole i obwód trójkąta.
W trójkąt równoramienny o podstawie 12 cm i wysokości 8 cm wpisano okrąg. Oblicz promień tego okręgu.
W trójkąt równoramienny o podstawie 24 cm i wysokości 5 cm wpisano okrąg. Oblicz promień tego okręgu.
W trójkącie równoramiennym kąt przy wierzchołku ma miarę 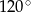 . Wyznacz stosunek długości promienia okręgu opisanego na tym trójkącie do długości promienia okręgu wpisanego w ten trójkąt.
. Wyznacz stosunek długości promienia okręgu opisanego na tym trójkącie do długości promienia okręgu wpisanego w ten trójkąt.
W trójkącie równoramiennym 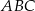 dane są
dane są 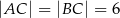 i
i 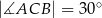 (zobacz rysunek). Oblicz wysokość
(zobacz rysunek). Oblicz wysokość 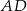 trójkąta opuszczoną z wierzchołka
trójkąta opuszczoną z wierzchołka 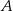 na bok
na bok 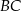 .
.
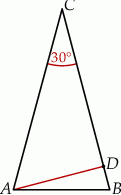
W trójkącie równoramiennym 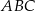 dane są
dane są 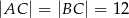 i
i 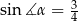 (zobacz rysunek). Oblicz wysokość
(zobacz rysunek). Oblicz wysokość 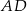 trójkąta opuszczoną z wierzchołka
trójkąta opuszczoną z wierzchołka 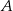 na bok
na bok 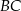 .
.
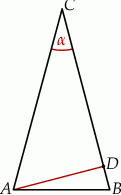
Punkt 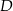 leży na boku
leży na boku 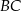 trójkąta równoramiennego
trójkąta równoramiennego 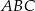 , w którym
, w którym 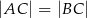 .
.
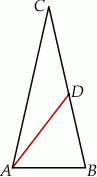
Odcinek 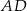 dzieli trójkąt
dzieli trójkąt 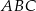 na dwa trójkąty równoramienne w taki sposób, że
na dwa trójkąty równoramienne w taki sposób, że 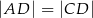 oraz
oraz 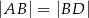 . Udowodnij, że
. Udowodnij, że 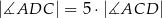 .
.
Punkt 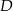 leży na boku
leży na boku 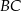 trójkąta równoramiennego, w którym
trójkąta równoramiennego, w którym 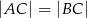 . Odcinek
. Odcinek 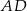 dzieli trójkąt
dzieli trójkąt 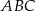 na dwa trójkąty równoramienne takie, że
na dwa trójkąty równoramienne takie, że 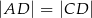 i
i 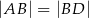 . Wykaż, że
. Wykaż, że 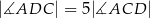 .
.
W trójkącie równoramiennym ostrokątnym 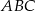 mamy dane
mamy dane 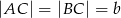 oraz
oraz 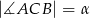 . Z wierzchołka
. Z wierzchołka 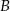 przez środek okręgu opisanego na tym trójkącie poprowadzono prostą, przecinającą bok
przez środek okręgu opisanego na tym trójkącie poprowadzono prostą, przecinającą bok 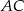 w punkcie
w punkcie 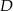 . Oblicz promień okręgu wpisanego w trójkąt
. Oblicz promień okręgu wpisanego w trójkąt 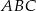 oraz długość odcinka
oraz długość odcinka 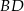 .
.
