Liczby 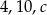 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny
Liczby 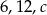 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Liczby 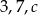 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Sinus kąta 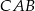 trójkąta równoramiennego
trójkąta równoramiennego 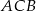 jest równy
jest równy 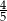 . Pole kwadratu
. Pole kwadratu 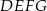 , wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta
, wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta 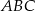 .
.
W trójkącie równoramiennym wysokość poprowadzona do podstawy ma długość 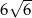 . Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.
. Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.
W trójkącie równoramiennym dane są długości podstawy 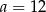 cm i wysokości
cm i wysokości 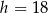 cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
Oblicz pole trójkąta równoramiennego, w którym odległość wierzchołka kąta prostego od przeciwprostokątnej jest równa 5 cm.
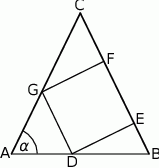
W trójkącie 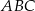 boki
boki 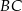 i
i 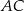 są równej długości. Prosta
są równej długości. Prosta 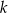 jest prostopadła do podstawy
jest prostopadła do podstawy 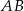 tego trójkąta i przecina boki
tego trójkąta i przecina boki 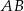 oraz
oraz 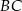 w punktach – odpowiednio –
w punktach – odpowiednio – 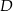 i
i 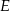 . Pole czworokąta
. Pole czworokąta 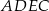 jest 17 razy większe od pola trójkąta
jest 17 razy większe od pola trójkąta 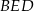 . Oblicz
. Oblicz 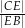 .
.
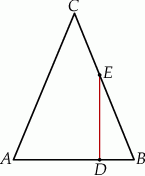
W trójkącie 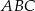 boki
boki 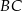 i
i 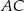 są równej długości. Prosta
są równej długości. Prosta 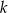 jest prostopadła do podstawy
jest prostopadła do podstawy 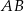 tego trójkąta i przecina boki
tego trójkąta i przecina boki 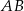 oraz
oraz 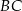 w punktach – odpowiednio –
w punktach – odpowiednio – 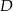 i
i 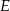 . Oblicz stosunek pola czworokąta
. Oblicz stosunek pola czworokąta 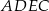 do pola trójkąta
do pola trójkąta 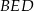 jeżeli
jeżeli 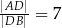 .
.
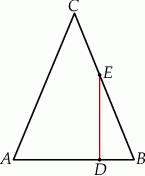
W trójkącie równoramiennym 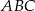 , w którym
, w którym 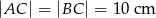 , wysokość poprowadzona z wierzchołka
, wysokość poprowadzona z wierzchołka 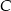 jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
Dany jest trójkąt 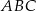 , w którym
, w którym 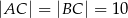 ,
, 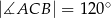 . Na boku
. Na boku 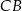 obrano punkt
obrano punkt 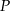 dzielący ten bok w stosunku 3:2 (licząc od punktu
dzielący ten bok w stosunku 3:2 (licząc od punktu 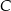 ). Oblicz sinus kąta
). Oblicz sinus kąta 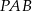 .
.
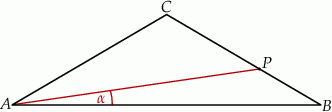
W trójkącie równoramiennym 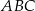 :
: 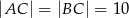 , a miara kąta
, a miara kąta 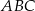 jest równa
jest równa 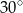 . Na boku
. Na boku 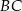 wybrano punkt
wybrano punkt 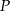 , taki, że
, taki, że 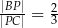 . Oblicz sinus kąta
. Oblicz sinus kąta  (zobacz rysunek).
(zobacz rysunek).
Podstawa 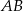 trójkąta równoramiennego
trójkąta równoramiennego 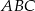 ma długość 8 oraz
ma długość 8 oraz 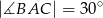 . Oblicz długość środkowej
. Oblicz długość środkowej 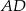 tego trójkąta.
tego trójkąta.
Oblicz pole trójkąta równoramiennego 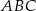 (patrz rysunek,
(patrz rysunek, 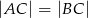 ), w którym wysokość
), w którym wysokość 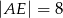 , a długość odcinka
, a długość odcinka 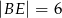 .
.
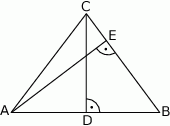
Oblicz pole trójkąta równoramiennego 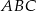 (patrz rysunek,
(patrz rysunek, 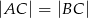 ), w którym wysokość
), w którym wysokość 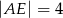 , a długość odcinka
, a długość odcinka 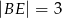 .
.
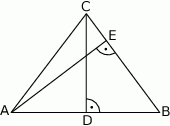
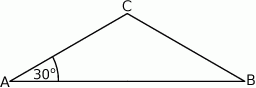
Kąt przy podstawie trójkąta równoramiennego 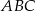 ma miarę
ma miarę 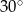 . Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta
. Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta  .
.
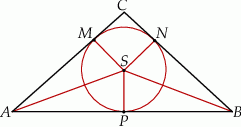
W trójkąt równoramienny 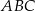 (
(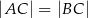 ) wpisano okrąg o środku
) wpisano okrąg o środku 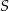 . Punkty wspólne okręgu i trójkąta oznaczono literami
. Punkty wspólne okręgu i trójkąta oznaczono literami 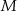 ,
, 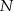 i
i 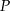 . Uzasadnij, że trójkąty
. Uzasadnij, że trójkąty 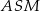 i
i 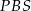 są przystające.
są przystające.
W trójkącie równoramiennym 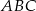 (
(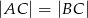 ) miara kąta
) miara kąta 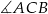 jest równa
jest równa 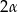 . Promień okręgu wpisanego w ten trójkąt ma długość
. Promień okręgu wpisanego w ten trójkąt ma długość  . Oblicz długości boków trójkąta
. Oblicz długości boków trójkąta 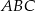 .
.
W trójkącie równoramiennym 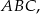 w którym
w którym 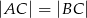 i
i 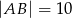 , poprowadzono dwusieczną kąta
, poprowadzono dwusieczną kąta 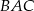 przecinająca bok
przecinająca bok 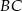 w punkcie
w punkcie 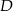 . Wówczas okazało się, że
. Wówczas okazało się, że 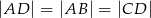 .
.
- Wyznacz miary kątów trójkąta
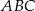 .
. - Oblicz długość ramienia
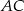 .
. - Oblicz
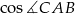 .
.
W trójkącie równoramiennym podstawa ma długość 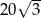 . Pole trójkąta jest równe
. Pole trójkąta jest równe 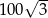 . Oblicz obwód tego trójkąta i miarę kąta przy podstawie.
. Oblicz obwód tego trójkąta i miarę kąta przy podstawie.
W trójkącie równoramiennym wysokość opuszczona na podstawę jest równa 36, a promień okręgu wpisanego w ten trójkąt jest równy 10. Oblicz długości boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
Dany jest trójkąt równoramienny 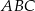 , w którym
, w którym 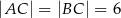 , a punkt
, a punkt 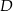 jest środkiem podstawy
jest środkiem podstawy 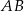 . Okrąg o środku
. Okrąg o środku 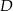 jest styczny do prostej
jest styczny do prostej 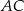 w punkcie
w punkcie 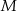 . Punkt
. Punkt 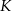 leży na boku
leży na boku 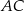 , punkt
, punkt 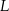 leży na boku
leży na boku 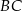 , odcinek
, odcinek 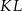 jest styczny do rozważanego okręgu oraz
jest styczny do rozważanego okręgu oraz 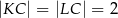 (zobacz rysunek).
(zobacz rysunek).
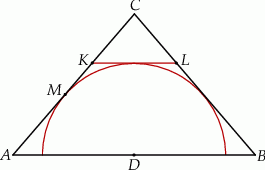
Wykaż, że 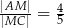 .
.
Dany jest trójkąt równoramienny 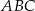 , w którym
, w którym 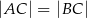 , a punkt
, a punkt 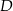 jest środkiem podstawy
jest środkiem podstawy 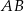 . Okrąg o środku
. Okrąg o środku 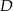 jest styczny do prostej
jest styczny do prostej 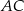 . Punkt
. Punkt 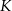 leży na boku
leży na boku 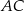 , punkt
, punkt 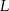 leży na boku
leży na boku 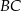 , odcinek
, odcinek 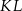 jest styczny do rozważanego okręgu oraz
jest styczny do rozważanego okręgu oraz 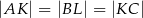 (zobacz rysunek).
(zobacz rysunek).
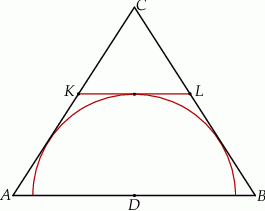
Wykaż, że trójkąt 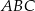 jest równoboczny.
jest równoboczny.
Dany jest trójkąt ostrokątny równoramienny 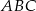 , w którym bok
, w którym bok 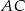 jest równy
jest równy 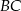 . Odcinek
. Odcinek 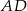 jest wysokością tego trójkąta, oraz odcinek
jest wysokością tego trójkąta, oraz odcinek 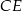 jest wysokością tego trójkąta. Udowodnij, że kąt
jest wysokością tego trójkąta. Udowodnij, że kąt 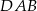 jest równy kątowi
jest równy kątowi 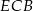 .
.
W trójkąt równoramienny, którego ramię jest równe 5 cm, a podstawa równa się 6 cm, wpisano prostokąt w ten sposób, że dwa jego wierzchołki leżą na podstawie, a pozostałe leżą na ramionach trójkąta. Wyznacz obwód i pole prostokąta jako funkcję jego wysokości.
W trójkącie równoramiennym kąt przy podstawie ma miarę  . Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na nim.
. Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na nim.

