Oblicz pole trójkąta równoramiennego 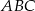 , w którym
, w którym 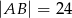 i
i 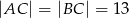 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny
Udowodnij, że w trójkącie równoramiennym środkowe poprowadzone do równych boków są równej długości.
Ostrokątny trójkąt równoramienny 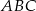 o podstawie
o podstawie 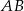 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 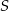 , przy czym kąt
, przy czym kąt 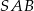 ma miarę
ma miarę 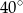 . Oblicz miarę kąta
. Oblicz miarę kąta 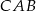 .
.
W trójkąt równoramienny 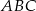 (
(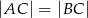 ) o długości podstawy
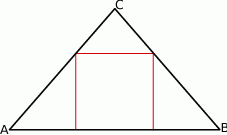
) o długości podstawy 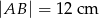 wpisano kwadrat o boku długości 5 cm. Oblicz pole trójkąta
wpisano kwadrat o boku długości 5 cm. Oblicz pole trójkąta  .
.
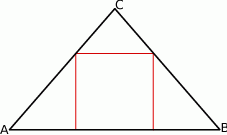
W trójkąt równoramienny  (
(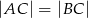 ) o długości podstawy
) o długości podstawy 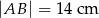 wpisano kwadrat o boku długości 6 cm. Oblicz pole trójkąta
wpisano kwadrat o boku długości 6 cm. Oblicz pole trójkąta 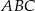 .
.
W trójkącie równoramiennym 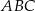 (
(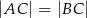 ) o kącie przy wierzchołku
) o kącie przy wierzchołku 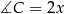 poprowadzono wysokość
poprowadzono wysokość 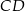 . Wiedząc, że
. Wiedząc, że 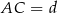 oblicz odległość środków okręgów wpisanych w trójkąty
oblicz odległość środków okręgów wpisanych w trójkąty 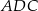 i
i 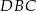 .
.
W trójkącie 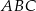 dane są:
dane są: 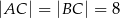 oraz
oraz 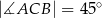 . Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka
. Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka 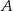 .
.
W trójkącie 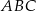 dane są:
dane są: 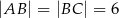 oraz
oraz 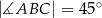 . Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka
. Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka 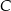 .
.
W trójkącie równoramiennym podstawa 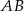 ma długość 8 cm. Promień okręgu, stycznego w punktach
ma długość 8 cm. Promień okręgu, stycznego w punktach 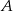 i
i 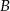 do prostych zawierających ramiona
do prostych zawierających ramiona 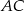 i
i 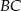 trójkąta, ma długość 5 cm. Oblicz pole trójkąta
trójkąta, ma długość 5 cm. Oblicz pole trójkąta 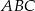 .
.
Dany jest trójkąt równoramienny 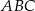 , w którym
, w którym 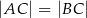 . Na ramieniu
. Na ramieniu 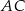 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 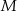 (
(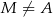 i
i 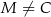 ), a na ramieniu
), a na ramieniu 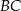 wybrano punkt
wybrano punkt 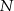 , w taki sposób, że
, w taki sposób, że 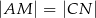 . Przez punkty
. Przez punkty 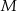 i
i 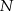 poprowadzono proste prostopadłe do podstawy
poprowadzono proste prostopadłe do podstawy 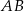 tego trójkąta, które wyznaczają na niej punkty
tego trójkąta, które wyznaczają na niej punkty 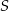 i
i 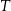 . Udowodnij, że
. Udowodnij, że 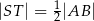 .
.
Dany jest trójkąt równoramienny 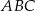 , w którym
, w którym 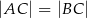 . Na ramieniu
. Na ramieniu 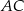 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 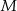 (
(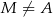 i
i 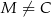 ), a na ramieniu
), a na ramieniu 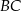 wybrano punkt
wybrano punkt 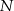 . Przez punkty
. Przez punkty 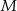 i
i 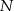 poprowadzono proste prostopadłe do podstawy
poprowadzono proste prostopadłe do podstawy 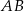 tego trójkąta, które wyznaczają na niej punkty
tego trójkąta, które wyznaczają na niej punkty 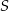 i
i 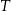 . Wykaż, że jeżeli
. Wykaż, że jeżeli 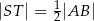 , to
, to 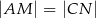 .
.
Odcinek 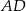 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 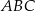 , w którym
, w którym 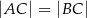 . Udowodnij, że
. Udowodnij, że 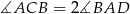 .
.
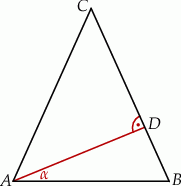
Wykaż, że miara kąta między wysokością trójkąta równoramiennego poprowadzoną do ramienia a podstawą tego trójkąta jest dwa razy mniejsza od miary kąta zawartego między ramionami tego trójkąta.
W trójkąt równoramienny 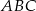 , w którym
, w którym 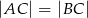 ,
, 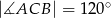 , wpisano okrąg, którego promień ma długość
, wpisano okrąg, którego promień ma długość  . Oblicz długości boków trójkąta.
. Oblicz długości boków trójkąta.
Miara kąta między ramionami trójkąta równoramiennego o polu 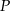 jest równa
jest równa  . Oblicz promień okręgu wpisanego w ten trójkąt.
. Oblicz promień okręgu wpisanego w ten trójkąt.
W trójkącie równoramiennym 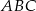 o podstawie
o podstawie 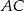 dane są:
dane są: 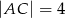 oraz
oraz 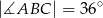 . Odcinek
. Odcinek 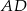 jest odcinkiem dwusiecznej kąta
jest odcinkiem dwusiecznej kąta 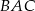 (zobacz rysunek).
(zobacz rysunek).
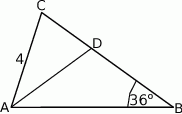
Oblicz długość odcinka 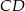 .
.
W trójkącie 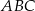 , w którym
, w którym 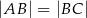 połączono wierzchołek
połączono wierzchołek 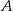 punktem
punktem 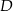 na boku
na boku 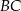 w ten sposób, że
w ten sposób, że 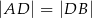 . Wyznacz miary kątów trójkąta
. Wyznacz miary kątów trójkąta 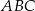 jeżeli
jeżeli 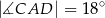 .
.
Wyznacz promień okręgu wpisanego w trójkąt równoramienny o ramieniu długości 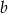 i kącie o mierze
i kącie o mierze  przy podstawie.
przy podstawie.
Liczby 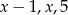 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
W trójkąt równoramienny o ramieniu 10 i podstawie 12 wpisano prostokąt o stosunku boków 1:4 w ten sposób, ze krótszy bok jest zawarty w podstawie trójkąta. Oblicz długości boków prostokąta.

