Przekrój osiowy stożka jest trójkątem równobocznym o polu 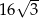 . Oblicz objętość i pole powierzchni całkowitej tego stożka.
. Oblicz objętość i pole powierzchni całkowitej tego stożka.
/Szkoła średnia/Geometria/Stereometria/Stożek/Pole powierzchni
Metalowy walec o objętości 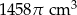 i przekroju będącym kwadratem przetopiono na stożek o takim samym promieniu podstawy, co walec. Oblicz stosunek pola powierzchni bocznej otrzymanego stożka do pola powierzchni bocznej wyjściowego walca.
i przekroju będącym kwadratem przetopiono na stożek o takim samym promieniu podstawy, co walec. Oblicz stosunek pola powierzchni bocznej otrzymanego stożka do pola powierzchni bocznej wyjściowego walca.
Cosinus kąta rozwarcia stożka jest równy 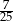 . Odległość środka kuli wpisanej w ten stożek od jego wierzchołka jest równa 10. Oblicz pole powierzchni bocznej stożka.
. Odległość środka kuli wpisanej w ten stożek od jego wierzchołka jest równa 10. Oblicz pole powierzchni bocznej stożka.
Dwie kule mające średnice 4 cm i 1 cm wpisano w stożek w ten sposób, że większa jest styczna do podstawy i powierzchni bocznej stożka, zaś mniejsza – do powierzchni bocznej stożka i do większej kuli. Oblicz pole powierzchni tego stożka.
Objętość stożka jest równa 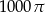 , a tworząca jest nachylona do podstawy pod kątem
, a tworząca jest nachylona do podstawy pod kątem 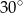 . Oblicz pole powierzchni bocznej tego stożka.
. Oblicz pole powierzchni bocznej tego stożka.
Objętość stożka jest równa 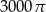 , a tworząca jest nachylona do podstawy pod kątem
, a tworząca jest nachylona do podstawy pod kątem 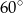 . Oblicz pole powierzchni bocznej tego stożka.
. Oblicz pole powierzchni bocznej tego stożka.
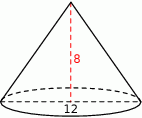
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości 12. Wysokość stożka jest równa 8. Oblicz pole powierzchni bocznej tego stożka.
Objętość stożka, w którym wysokość jest równa promieniowi podstawy, jest równa 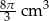 . Oblicz pole powierzchni całkowitej tego stożka. Przyjmując przybliżenie
. Oblicz pole powierzchni całkowitej tego stożka. Przyjmując przybliżenie 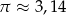 podaj wynik z dokładnością do 0,1.
podaj wynik z dokładnością do 0,1.
W stożek o wysokości 10 wpisano kulę o promieniu 4. Oblicz pole powierzchni całkowitej stożka.
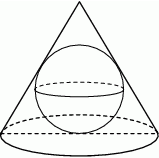
Dany jest stożek o objętości 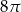 , w którym stosunek wysokości do promienia podstawy jest równy 3:8. Oblicz pole powierzchni bocznej tego stożka.
, w którym stosunek wysokości do promienia podstawy jest równy 3:8. Oblicz pole powierzchni bocznej tego stożka.
Dany jest stożek o objętości 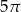 , w którym stosunek wysokości do promienia podstawy jest równy 5:9. Oblicz pole powierzchni bocznej tego stożka.
, w którym stosunek wysokości do promienia podstawy jest równy 5:9. Oblicz pole powierzchni bocznej tego stożka.
Kąt rozwarcia stożka jest równy 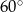 . Promień podstawy stożka ma długość 4. Oblicz pole powierzchni bocznej stożka.
. Promień podstawy stożka ma długość 4. Oblicz pole powierzchni bocznej stożka.
Tworząca stożka jest nachylona do podstawy pod kątem  . Kula opisana na tym stożku ma promień
. Kula opisana na tym stożku ma promień 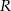 . Oblicz pole powierzchni całkowitej tego stożka.
. Oblicz pole powierzchni całkowitej tego stożka.

