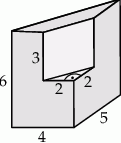
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.

Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
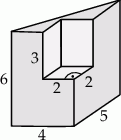
Podstawą graniastosłupa prostego jest trójkąt 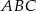 o bokach mających długość 5,7,8. Oblicz cosinusy kątów, jakie tworzą dwie kolejne ściany boczne tego graniastosłupa.
o bokach mających długość 5,7,8. Oblicz cosinusy kątów, jakie tworzą dwie kolejne ściany boczne tego graniastosłupa.
Podstawą graniastosłupa prostego o objętości 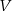 jest równoległobok o bokach długości
jest równoległobok o bokach długości  i
i 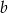 . Wykaż, że pole powierzchni bocznej tego graniastosłupa jest nie mniejsze niż
. Wykaż, że pole powierzchni bocznej tego graniastosłupa jest nie mniejsze niż 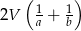 .
.
Dany jest graniastosłup czworokątny prosty 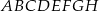 o podstawach
o podstawach 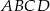 i
i 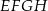 oraz krawędziach bocznych
oraz krawędziach bocznych 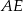 ,
, 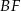 ,
, 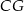 ,
, 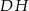 . Podstawa
. Podstawa 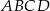 graniastosłupa jest rombem o boku długości 8 cm i kątach ostrych
graniastosłupa jest rombem o boku długości 8 cm i kątach ostrych 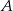 i
i 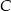 o mierze
o mierze 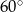 . Przekątna graniastosłupa
. Przekątna graniastosłupa 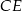 jest nachylona do płaszczyzny podstawy pod kątem
jest nachylona do płaszczyzny podstawy pod kątem 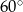 . Sporządź rysunek pomocniczy i zaznacz na nim wymienione w zadaniu kąty. Oblicz objętość tego graniastosłupa.
. Sporządź rysunek pomocniczy i zaznacz na nim wymienione w zadaniu kąty. Oblicz objętość tego graniastosłupa.
Podstawą graniastosłupa prostego jest romb. Krótsza przekątna rombu tworzy z krawędzią podstawy kąt 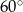 i ma długość
i ma długość 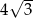 . Dłuższa przekątna graniastosłupa tworzy z dłuższą przekątną rombu kąt
. Dłuższa przekątna graniastosłupa tworzy z dłuższą przekątną rombu kąt 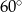 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
W graniastosłupie prostym o podstawie rombu krótsza przekątna podstawy ma długość 6 cm i tworzy z krawędzią podstawy kąt 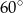 . Kąt między krótszą przekątną rombu i krótszą przekątną graniastosłupa ma miarę
. Kąt między krótszą przekątną rombu i krótszą przekątną graniastosłupa ma miarę 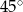 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
Podstawą graniastosłupa prostego 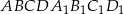 jest trapez równoramienny
jest trapez równoramienny 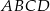 wpisany w okrąg o środku
wpisany w okrąg o środku 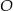 i promieniu
i promieniu 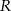 . Dłuższa podstawa
. Dłuższa podstawa 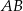 trapezu jest średnicą tego okręgu, a krótsza ma długość
trapezu jest średnicą tego okręgu, a krótsza ma długość  (zobacz rysunek). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze
(zobacz rysunek). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze  . Wyznacz objętość tego graniastosłupa jako funkcję promienia
. Wyznacz objętość tego graniastosłupa jako funkcję promienia 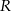 , długości podstawy
, długości podstawy  i miary kąta
i miary kąta  .
.
Podstawą graniastosłupa prostego jest romb, którego krótsza przekątna ma długość  , a kąt ostry miarę
, a kąt ostry miarę 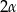 . Pole przekroju wyznaczonego przez krawędź boczną graniastosłupa i dłuższą przekątną podstawy wynosi
. Pole przekroju wyznaczonego przez krawędź boczną graniastosłupa i dłuższą przekątną podstawy wynosi 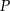 . Oblicz długość dłuższej przekątnej graniastosłupa, wykonaj rysunek bryły i zaznacz w nim właściwy przekrój.
. Oblicz długość dłuższej przekątnej graniastosłupa, wykonaj rysunek bryły i zaznacz w nim właściwy przekrój.
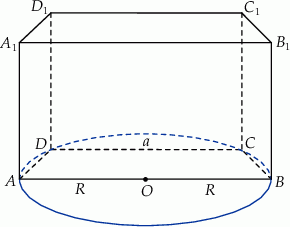
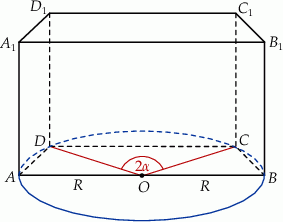
Podstawą graniastosłupa prostego 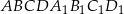 jest trapez równoramienny
jest trapez równoramienny 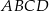 wpisany w okrąg o środku
wpisany w okrąg o środku 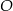 i promieniu
i promieniu 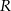 . Dłuższa podstawa
. Dłuższa podstawa 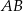 trapezu jest średnicą tego okręgu, a krótsza – cięciwą odpowiadającą kątowi środkowemu o mierze
trapezu jest średnicą tego okręgu, a krótsza – cięciwą odpowiadającą kątowi środkowemu o mierze 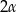 (zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze
(zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze  . Wyznacz objętość tego graniastosłupa jako funkcję promienia
. Wyznacz objętość tego graniastosłupa jako funkcję promienia 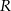 i miary kąta
i miary kąta  .
.
Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę 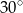 . Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
. Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
Podstawą graniastosłupa prostego jest trójkąt prostokątny równoramienny o ramieniu długości 9. Kąt między przekątną największej ściany bocznej i wysokością graniastosłupa jest równy 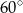 . Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
. Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
Podstawą graniastosłupa jest trójkąt prostokątny równoramienny o ramieniu długości 6. Kąt między przekątną największej ściany bocznej i wysokością graniastosłupa jest równy 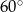 . Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
. Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
Dany jest graniastosłup, którego podstawą jest równoległobok o polu 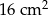 i kącie ostrym
i kącie ostrym 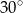 . Oblicz objętość graniastosłupa jeżeli pola jego ścian są równe
. Oblicz objętość graniastosłupa jeżeli pola jego ścian są równe 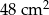 i
i 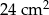 .
.
