Oblicz objętość i pole powierzchni graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 6 cm i 8 cm, którego przekątna ściany bocznej tworzy z krawędzią podstawy kąt o mierze 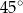 .
.
/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Dowolny
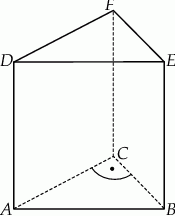
Podstawą graniastosłupa prostego 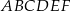 jest trójkąt
jest trójkąt 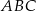 , w którym
, w którym 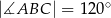 oraz
oraz 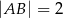 (zobacz rysunek). Trójkąt
(zobacz rysunek). Trójkąt 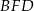 jest równoboczny. Oblicz pole powierzchni całkowitej tego graniastosłupa.
jest równoboczny. Oblicz pole powierzchni całkowitej tego graniastosłupa.
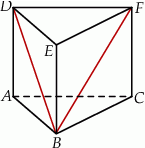
Podstawą graniastosłupa prostego 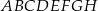 jest romb o boku długości 5, polu 24 i kącie ostrym
jest romb o boku długości 5, polu 24 i kącie ostrym 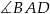 . Graniastosłup ten przecięto płaszczyzną
. Graniastosłup ten przecięto płaszczyzną 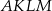 w ten sposób, że otrzymany przekrój jest rombem o kącie ostrym
w ten sposób, że otrzymany przekrój jest rombem o kącie ostrym 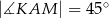 (zobacz rysunek). Oblicz pole tego przekroju.
(zobacz rysunek). Oblicz pole tego przekroju.
Trójkąt o bokach 3, 5, 7 jest podstawą graniastosłupa prostego, w który wpisano kulę. Oblicz objętość tego graniastosłupa.
Podstawą ostrosłupa trójkątnego 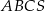 jest trójkąt prostokątny
jest trójkąt prostokątny 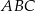 , w którym
, w którym 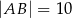 . Stosunek długości przyprostokątnej
. Stosunek długości przyprostokątnej 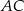 tego trójkąta do długości przyprostokątnej
tego trójkąta do długości przyprostokątnej 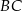 jest równy 4:3. Wszystkie krawędzie boczne ostrosłupa mają długość 13. Oblicz objętość tego ostrosłupa.
jest równy 4:3. Wszystkie krawędzie boczne ostrosłupa mają długość 13. Oblicz objętość tego ostrosłupa.
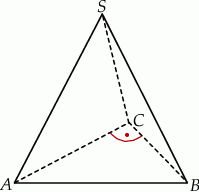
Podstawą graniastosłupa prostego jest trójkąt prostokątny o przyprostokątnych mających długości 1 i 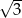 . Podaj miary kątów między sąsiednimi ścianami bocznymi tego graniastosłupa.
. Podaj miary kątów między sąsiednimi ścianami bocznymi tego graniastosłupa.
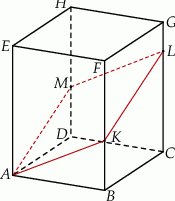
Dany jest graniastosłup prosty 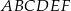 , którego podstawą jest trójkąt
, którego podstawą jest trójkąt 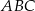 o kątach
o kątach 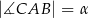 i
i 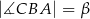 . Przekątne
. Przekątne 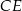 i
i 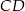 ścian bocznych tworzą kąt o mierze
ścian bocznych tworzą kąt o mierze 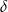 takiej, że
takiej, że 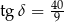 (zobacz rysunek).
(zobacz rysunek).
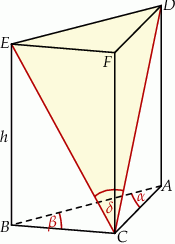
Pole trójkąta 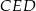 jest równe 4, a pole trójkąta
jest równe 4, a pole trójkąta 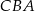 jest równe
jest równe 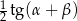 . Oblicz wysokość
. Oblicz wysokość 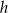 tego graniastosłupa.
tego graniastosłupa.
Liczba wszystkich przekątnych podstaw i ścian bocznych pewnego graniastosłupa jest równa 110. Oblicz, ile krawędzi ma podstawa tego graniastosłupa.
Podstawą graniastosłupa prostego 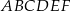 jest trójkąt równoramienny
jest trójkąt równoramienny 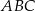 , w którym
, w którym 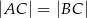 ,
, 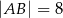 . Wysokość trójkąta
. Wysokość trójkąta 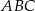 , poprowadzona z wierzchołka
, poprowadzona z wierzchołka 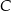 , ma długość 3. Przekątna
, ma długość 3. Przekątna 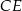 ściany bocznej tworzy z krawędzią
ściany bocznej tworzy z krawędzią 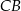 podstawy
podstawy 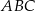 kąt
kąt 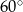 (zobacz rysunek).
(zobacz rysunek).
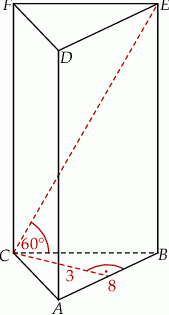
Oblicz pole powierzchni całkowitej oraz objętość tego graniastosłupa.
Podstawą graniastosłupa prostego jest trójkąt prostokątny równoramienny. Kąt między przekątnymi, wychodzącymi z tego samego wierzchołka, dwóch prostopadłych ścian bocznych, ma miarę 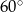 . Wiedząc, że objętość tego graniastosłupa jest równa
. Wiedząc, że objętość tego graniastosłupa jest równa 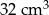 , oblicz pole powierzchni całkowitej tej bryły.
, oblicz pole powierzchni całkowitej tej bryły.
Oblicz objętość graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 16 cm i 30 cm, a krawędź boczna jest dwa razy dłuższa od krawędzi podstawy.
Dany jest graniastosłup prosty o podstawie pięciokątnej 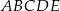 (zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu dwa razy mniejszym niż pole pięciokąta
(zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu dwa razy mniejszym niż pole pięciokąta 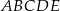 . Pole powierzchni całkowitej tego graniastosłupa jest równe 153. Oblicz jego objętość.
. Pole powierzchni całkowitej tego graniastosłupa jest równe 153. Oblicz jego objętość.
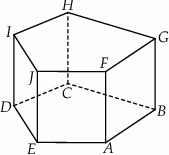
Dany jest graniastosłup prosty o podstawie sześciokątnej 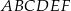 (zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu o 25% mniejszym niż pole sześciokąta
(zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu o 25% mniejszym niż pole sześciokąta 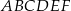 . Pole powierzchni całkowitej tego graniastosłupa jest równe 156. Oblicz jego objętość.
. Pole powierzchni całkowitej tego graniastosłupa jest równe 156. Oblicz jego objętość.
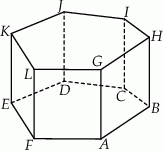
Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości  . Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Uzasadnij, że wysokość graniastosłupa jest nie większa niż
. Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Uzasadnij, że wysokość graniastosłupa jest nie większa niż 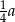 .
.
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni tej bryły.
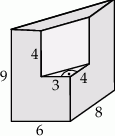
Podstawą graniastosłupa jest trapez równoramienny o podstawach długości 56 cm i 40 cm oraz wysokości 15 cm. Wiedząc, że wysokość graniastosłupa jest równa 10 cm, oblicz jego pole powierzchni całkowitej.
Podstawą graniastosłupa jest trapez równoramienny o podstawach długości 56 cm i 40 cm oraz wysokości 15 cm. Wiedząc, że wysokość graniastosłupa jest równa 20 cm, oblicz jego pole powierzchni całkowitej.
Podstawą graniastosłupa prostego 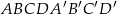 jest romb
jest romb 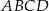 . Przekątna
. Przekątna 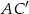 tego graniastosłupa ma długość 8 i jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa ma długość 8 i jest nachylona do płaszczyzny podstawy pod kątem 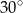 , a przekątna
, a przekątna 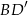 jest nachylona do tej płaszczyzny pod kątem
jest nachylona do tej płaszczyzny pod kątem 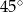 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
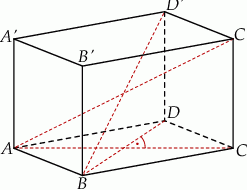
Podstawą graniastosłupa prostego  jest romb
jest romb  . Przekątna
. Przekątna 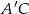 tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem 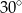 , a objętość graniastosłupa jest równa
, a objętość graniastosłupa jest równa 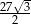 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
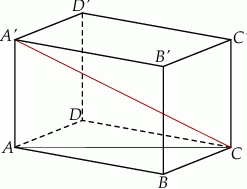
Podstawą graniastosłupa prostego 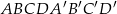 jest romb
jest romb 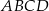 . Przekątna
. Przekątna 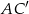 tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem 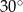 , a przekątna
, a przekątna 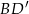 ma długość
ma długość 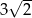 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
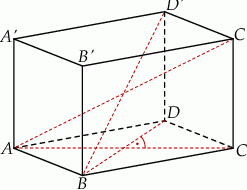
Każda krawędź graniastosłupa trójkątnego ma długość 26. Ściana boczna 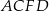 jest prostopadła do płaszczyzny podstawy
jest prostopadła do płaszczyzny podstawy 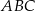 , a krawędź
, a krawędź 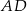 jest nachylona do płaszczyzny podstawy pod katem
jest nachylona do płaszczyzny podstawy pod katem  takim, że
takim, że 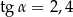 (zobacz rysunek).
(zobacz rysunek).
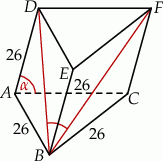
Oblicz cosinus kąta 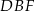 .
.
Podstawą graniastosłupa prostego 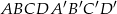 jest równoległobok
jest równoległobok 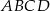 o bokach długości
o bokach długości 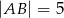 i
i 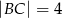 . Oblicz długość wysokości
. Oblicz długość wysokości 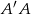 graniastosłupa jeżeli
graniastosłupa jeżeli 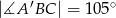 oraz
oraz 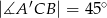 .
.
Każda ściana graniastosłupa jest rombem o boku długości  i kącie ostrym o mierze
i kącie ostrym o mierze 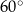 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
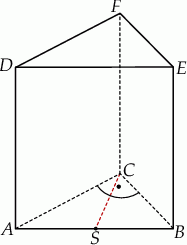
Podstawą graniastosłupa prostego 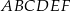 jest trójkąt prostokątny
jest trójkąt prostokątny 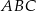 , w którym
, w którym 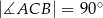 (zobacz rysunek). Stosunek długości przyprostokątnej
(zobacz rysunek). Stosunek długości przyprostokątnej 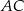 tego trójkąta do długości przyprostokątnej
tego trójkąta do długości przyprostokątnej 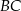 jest równy 4:3. Punkt
jest równy 4:3. Punkt 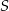 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 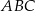 , a długość odcinka
, a długość odcinka 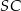 jest równa 5. Pole ściany bocznej
jest równa 5. Pole ściany bocznej 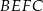 graniastosłupa jest równe 48. Oblicz objętość tego graniastosłupa.
graniastosłupa jest równe 48. Oblicz objętość tego graniastosłupa.
Podstawą graniastosłupa prostego 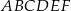 jest trójkąt prostokątny
jest trójkąt prostokątny 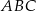 , w którym
, w którym 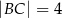 . Promień okręgu opisanego na trójkącie
. Promień okręgu opisanego na trójkącie 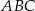 ma długość 3, a sinus kąta nachylenia przekątnej
ma długość 3, a sinus kąta nachylenia przekątnej 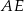 ściany bocznej
ściany bocznej 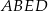 do płaszczyzny podstawy jest równy
do płaszczyzny podstawy jest równy 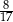 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.