Dane są dwa przeciwległe wierzchołki kwadratu 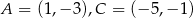 . Wyznacz obwód tego kwadratu.
. Wyznacz obwód tego kwadratu.
/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Kwadrat
Dane są dwa przeciwległe wierzchołki kwadratu 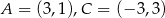 . Oblicz obwód tego kwadratu.
. Oblicz obwód tego kwadratu.
Wierzchołkami kwadratu 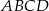 są punkty o współrzędnych
są punkty o współrzędnych 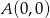 ,
, 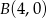 ,
, 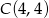 i
i 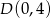 . Dla każdej liczby rzczywistej
. Dla każdej liczby rzczywistej 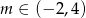 rozważamy trójkąt o wierzchołkach
rozważamy trójkąt o wierzchołkach 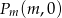 ,
, 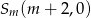 i
i 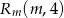 . Wyznacz wszystkie wartości prametru
. Wyznacz wszystkie wartości prametru 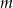 , dla których pole figury, która jest częścią wspólną kwadratu
, dla których pole figury, która jest częścią wspólną kwadratu 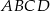 i trójkąta
i trójkąta 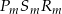 wynosi 2.
wynosi 2.
Dane są współrzędne dwóch kolejnych wierzchołków kwadratu 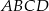 :
: 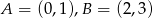 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 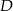 , jeśli wiesz, że kwadrat jest zawarty w I i II ćwiartce układu współrzędnych.
, jeśli wiesz, że kwadrat jest zawarty w I i II ćwiartce układu współrzędnych.
Dany jest kwadrat 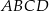 , w którym
, w którym 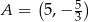 . Przekątna
. Przekątna 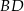 tego kwadratu jest zawarta w prostej o równaniu
tego kwadratu jest zawarta w prostej o równaniu 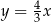 . Oblicz współrzędne punktu przecięcia przekątnych
. Oblicz współrzędne punktu przecięcia przekątnych 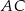 i
i 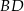 oraz pole kwadratu
oraz pole kwadratu 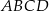 .
.
Dany jest kwadrat 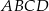 , w którym
, w którym 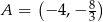 . Przekątna
. Przekątna 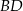 tego kwadratu jest zawarta w prostej o równaniu
tego kwadratu jest zawarta w prostej o równaniu 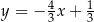 . Oblicz współrzędne punktu przecięcia przekątnych
. Oblicz współrzędne punktu przecięcia przekątnych 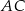 i
i 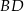 oraz pole kwadratu
oraz pole kwadratu 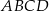 .
.
Kwadrat 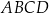 jest wpisany w okrąg o równaniu
jest wpisany w okrąg o równaniu 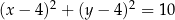 oraz
oraz 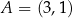 . Wyznacz równanie prostej zawierającej przekątną
. Wyznacz równanie prostej zawierającej przekątną 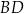 tego kwadratu.
tego kwadratu.
Jeden z boków kwadratu 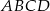 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 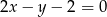 . Wierzchołek
. Wierzchołek 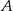 ma współrzędne
ma współrzędne 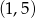 .
.
- Znajdź współrzędne pozostałych wierzchołków.
- Oblicz pole kwadratu
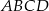 .
.
Jeden bok kwadratu opisanego okręgu o równaniu 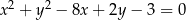 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 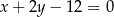 . Oblicz współrzędne wierzchołków tego kwadratu.
. Oblicz współrzędne wierzchołków tego kwadratu.
Dwa boki kwadratu zawierają się w prostych o równaniach 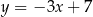 i
i 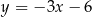 . Oblicz pole tego kwadratu.
. Oblicz pole tego kwadratu.
W kwadracie 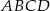 dane są wierzchołek
dane są wierzchołek 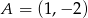 i środek symetrii
i środek symetrii 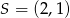 . Oblicz pole kwadratu
. Oblicz pole kwadratu 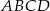 .
.
Bok 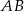 kwadratu
kwadratu 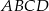 o polu równym 4 jest zawarty w prostej o równaniu
o polu równym 4 jest zawarty w prostej o równaniu 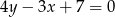 . Wiadomo ponadto, że wewnątrz tego kwadratu leży początek układu współrzędnych. Napisz równanie prostej zawierającej bok
. Wiadomo ponadto, że wewnątrz tego kwadratu leży początek układu współrzędnych. Napisz równanie prostej zawierającej bok 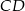 tego kwadratu.
tego kwadratu.
Mając dane współrzędne punktu 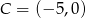 kwadratu
kwadratu 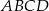 oraz współrzędne punktu przecięcia się przekątnych
oraz współrzędne punktu przecięcia się przekątnych 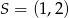 , wyznacz współrzędne pozostałych wierzchołków kwadratu
, wyznacz współrzędne pozostałych wierzchołków kwadratu 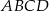 .
.
Punkt 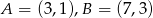 są kolejnymi wierzchołkami kwadratu
są kolejnymi wierzchołkami kwadratu 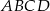 . Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.
. Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.
Dany jest kwadrat 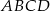 o polu 10 i wierzchołku
o polu 10 i wierzchołku 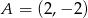 . Przekątna
. Przekątna 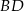 tego kwadratu ma równanie
tego kwadratu ma równanie 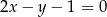 . Oblicz współrzędne pozostałych wierzchołków kwadratu.
. Oblicz współrzędne pozostałych wierzchołków kwadratu.
Wyznacz równanie okręgu wpisanego w kwadrat 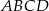 , gdzie
, gdzie 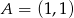 i
i 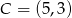 .
.
W okrąg o równaniu 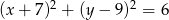 wpisano kwadrat. Oblicz pole tego kwadratu.
wpisano kwadrat. Oblicz pole tego kwadratu.
Wykaż, że punkt o współrzędnych 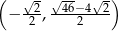 jest wierzchołkiem kwadratu opisanego na okręgu o równaniu
jest wierzchołkiem kwadratu opisanego na okręgu o równaniu
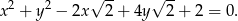
Przekątne kwadratu 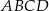 przecinają się w punkcie
przecinają się w punkcie 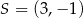 , a jeden z jego boków jest zawarty w prostej
, a jeden z jego boków jest zawarty w prostej 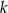 o równaniu
o równaniu 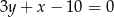 . Wyznacz współrzędne wierzchołków kwadratu
. Wyznacz współrzędne wierzchołków kwadratu 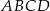 .
.
W kwadracie 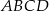 dane są wierzchołek
dane są wierzchołek 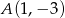 i równanie prostej
i równanie prostej 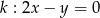 w której zawiera się jedna z przekątnych kwadratu. Znajdź współrzędne wierzchołka
w której zawiera się jedna z przekątnych kwadratu. Znajdź współrzędne wierzchołka 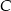 oraz oblicz pole tego kwadratu.
oraz oblicz pole tego kwadratu.
Wierzchołki 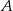 i
i 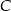 kwadratu
kwadratu 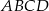 o polu 8 leżą na prostej o równaniu
o polu 8 leżą na prostej o równaniu 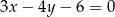 . Środek symetrii tego kwadratu ma współrzędne
. Środek symetrii tego kwadratu ma współrzędne 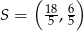 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 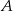 i
i 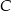 .
.
Wyznacz współrzędne środka okręgu opisanego na kwadracie, którego jeden z boków jest zawarty w prostej o równaniu 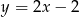 , a punkt
, a punkt 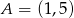 jest jego wierzchołkiem. Rozważ wszystkie przypadki.
jest jego wierzchołkiem. Rozważ wszystkie przypadki.

