W pewnym zakładzie pracy zależność przychodów ze sprzedaży od wielkości produkcji wyraża w przybliżeniu wzór 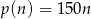 , gdzie
, gdzie  oznacza liczbę sztuk wyprodukowanego towaru, a koszty produkcji, w złotych, określa zależność
oznacza liczbę sztuk wyprodukowanego towaru, a koszty produkcji, w złotych, określa zależność 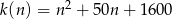 .
.
- Napisz wzór funkcji
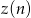 - zależności zysku zakładu od wielkości produkcji, jeśli wiadomo, że zysk jest różnicą między przychodem zakładu a kosztami produkcji.
- zależności zysku zakładu od wielkości produkcji, jeśli wiadomo, że zysk jest różnicą między przychodem zakładu a kosztami produkcji. - Przy jakiej wielkości produkcji zysk wynosi 0?
- Jaka wielkość produkcji zapewnia największy zysk? Jaki jest koszt produkcji, gdy zysk jest największy?

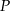 (w złotych) z tygodniowej sprzedaży
(w złotych) z tygodniowej sprzedaży  wiatraków można opisać funkcją
wiatraków można opisać funkcją 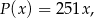
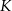 (w złotych) produkcji
(w złotych) produkcji  wiatraków w ciągu jednego tygodnia można określić funkcją
wiatraków w ciągu jednego tygodnia można określić funkcją 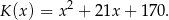
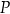 (w złotych) ze sprzedaży
(w złotych) ze sprzedaży  krzeseł można opisać funkcją
krzeseł można opisać funkcją 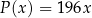
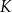 (w złotych) produkcji
(w złotych) produkcji  krzeseł dziennie można opisać funkcją
krzeseł dziennie można opisać funkcją 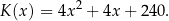
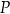 (w złotych) ze sprzedaży
(w złotych) ze sprzedaży  stołów można opisać funkcją
stołów można opisać funkcją 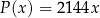
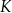 (w złotych) produkcji
(w złotych) produkcji  stołów miesięcznie można opisać funkcją
stołów miesięcznie można opisać funkcją 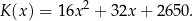
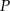 (w złotych) z tygodniowej sprzedaży
(w złotych) z tygodniowej sprzedaży  kwietników można opisać funkcją
kwietników można opisać funkcją 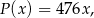
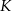 (w złotych) produkcji
(w złotych) produkcji  kwietników w ciągu jednego tygodnia można określić funkcją
kwietników w ciągu jednego tygodnia można określić funkcją 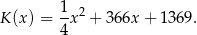
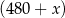 litrów dziennie przeciętny koszt
litrów dziennie przeciętny koszt 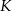 (w złotych) wytworzenia jednego litra oleju jest równy
(w złotych) wytworzenia jednego litra oleju jest równy ![22x 2 − 62 1,5x + 23430 K(x ) = -----------------------, gdzie x ∈ [0,50] 480+ x](https://img.zadania.info/zad/8271275/HzadT2x.gif)
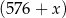 kart graficznych dziennie przeciętny koszt
kart graficznych dziennie przeciętny koszt 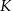 (w złotych) wytworzenia jednej karty jest równy
(w złotych) wytworzenia jednej karty jest równy ![2 K (x) = 2-3x-−--103,5x-+-42-4764, gdzie x ∈ [0,44] 576+ x](https://img.zadania.info/zad/3502777/HzadT2x.gif)
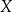 wytwarza pewien produkt
wytwarza pewien produkt 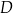 . Badania rynku pokazały, że związek między ilością
. Badania rynku pokazały, że związek między ilością 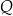 produktu
produktu 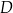 , jaką firma jest w stanie zbyć na rynku, a ceną
, jaką firma jest w stanie zbyć na rynku, a ceną 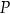 produktu jest następujący:
produktu jest następujący: ![P(Q ) = 90 − 0,1Q , dla Q ∈ [0 ,900],](https://img.zadania.info/zad/8691373/HzadT5x.png)
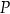 jest ceną za jednostkę produktu w złotych, a
jest ceną za jednostkę produktu w złotych, a 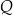 – ilością produktu w tys. sztuk.
– ilością produktu w tys. sztuk. 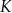 wytworzenia
wytworzenia 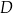 produktu
produktu 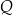 zależą od ilości
zależą od ilości 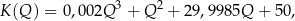 wytwarzanego produktu następująco:
wytwarzanego produktu następująco: 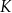
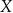 jest kosztem produkcji
jest kosztem produkcji 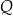 produktów
produktów 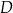 w tys. zł. Oblicz, przy jakiej wielkości produkcji firma
w tys. zł. Oblicz, przy jakiej wielkości produkcji firma 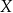 osiąga największy dochód. Wynik podaj zaokrąglony z dokładnością do 100 sztuk.
osiąga największy dochód. Wynik podaj zaokrąglony z dokładnością do 100 sztuk. 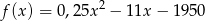 , gdzie
, gdzie  oznacza liczbę sprzedanych akumulatorów.
oznacza liczbę sprzedanych akumulatorów. 