Wykaż, że dla dowolnych liczb rzeczywistych  ,
, 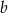 i
i  , funkcja
, funkcja
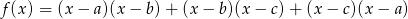
ma co najmniej jedno miejsce zerowe.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla dowolnych liczb rzeczywistych  ,
, 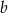 i
i  , funkcja
, funkcja
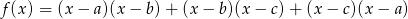
ma co najmniej jedno miejsce zerowe.
Dane są liczby wymierne 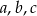 takie, że równanie
takie, że równanie 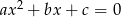 ma dwa rozwiązania rzeczywiste. Uzasadnij, że jeżeli jeden z pierwiastków tego równania jest liczbą wymierną to drugi pierwiastek też jest liczbą wymierną.
ma dwa rozwiązania rzeczywiste. Uzasadnij, że jeżeli jeden z pierwiastków tego równania jest liczbą wymierną to drugi pierwiastek też jest liczbą wymierną.
Dane są niezerowe liczby wymierne 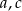 takie, że funkcja
takie, że funkcja 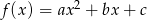 ma miejsce zerowe będące liczbą wymierną. Wykaż, że
ma miejsce zerowe będące liczbą wymierną. Wykaż, że 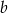 jest liczbą wymierną.
jest liczbą wymierną.
Wykaż, że jeżeli 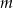 i
i  są takimi liczbami całkowitymi, że rozwiązania równania
są takimi liczbami całkowitymi, że rozwiązania równania 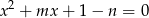 są niezerowymi liczbami całkowitymi, to liczba
są niezerowymi liczbami całkowitymi, to liczba 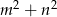 nie jest liczbą pierwszą.
nie jest liczbą pierwszą.
Wykaż że jeśli 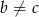 i funkcje kwadratowe
i funkcje kwadratowe 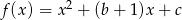 oraz
oraz 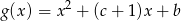 mają wspólne miejsce zerowe, to
mają wspólne miejsce zerowe, to 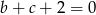 .
.
Wykaż, że jeżeli funkcje 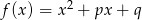 i
i 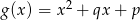 , gdzie
, gdzie 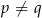 , mają wspólne miejsce zerowe, to
, mają wspólne miejsce zerowe, to 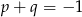 .
.
Wykaż, że funkcja kwadratowa 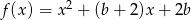 , ma co najmniej jedno miejsce zerowe dla każdej wartości parametru
, ma co najmniej jedno miejsce zerowe dla każdej wartości parametru 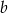 . Dla jakiej wartości parametru
. Dla jakiej wartości parametru 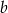 funkcja ma tylko jedno miejsce zerowe? Wyznacz to miejsce.
funkcja ma tylko jedno miejsce zerowe? Wyznacz to miejsce.
Uzasadnij, że równanie 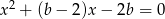 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej 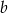 ma przynajmniej jedno rozwiązanie.
ma przynajmniej jedno rozwiązanie.
Wykaż, że jeżeli między współczynnikami trójmianów 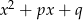 i
i 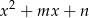 zachodzi związek
zachodzi związek 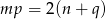 , to przynajmniej jedno z równań
, to przynajmniej jedno z równań 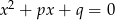 lub
lub 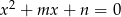 ma rozwiązanie.
ma rozwiązanie.
Uzasadnij, że dla dowolnej liczby całkowitej 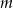 rozwiązania równania
rozwiązania równania 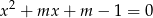 z niewiadomą
z niewiadomą  są liczbami całkowitymi.
są liczbami całkowitymi.
Wykaż, że funkcja kwadratowa 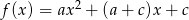 ma co najmniej jedno miejsce zerowe dla
ma co najmniej jedno miejsce zerowe dla 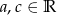 i
i 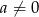 .
.
Wykaż, że jeśli funkcja kwadratowa 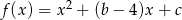 osiąga najmniejszą wartość dla argumentu
osiąga najmniejszą wartość dla argumentu  , to ma dwa rózne miejsca zerowe wtedy i tylko wtedy, gdy
, to ma dwa rózne miejsca zerowe wtedy i tylko wtedy, gdy 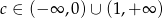 .
.
Dana jest funkcja kwadratowa 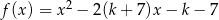 określona dla dowolnego
określona dla dowolnego 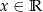 . Wykaż, że jeżeli funkcja
. Wykaż, że jeżeli funkcja 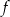 ma dwa różne miejsca zerowe:
ma dwa różne miejsca zerowe: 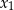 i
i 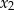 , to miejscami zerowymi funkcji
, to miejscami zerowymi funkcji 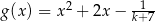 , określonej dla
, określonej dla 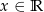 , są liczby
, są liczby 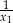 i
i 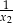 .
.
Liczby 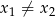 są dwoma dodatnimi pierwiastkami równania
są dwoma dodatnimi pierwiastkami równania 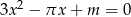 z niewiadomą
z niewiadomą  , gdzie
, gdzie 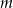 jest pewną ustaloną liczbą rzeczywistą.
jest pewną ustaloną liczbą rzeczywistą.
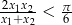 .
. 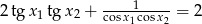 .
.Wykaż, że dla dowolnych liczb rzeczywistych  ,
, 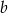 ,
,  równanie
równanie 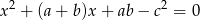 ma co najmniej jedno rozwiązanie. Kiedy równanie ma dokładnie jedno rozwiązanie?
ma co najmniej jedno rozwiązanie. Kiedy równanie ma dokładnie jedno rozwiązanie?
Wykaż, że dla dowolnej liczby rzeczywistej 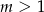 istnieje dokładnie jedna liczba rzeczywista
istnieje dokładnie jedna liczba rzeczywista  taka, że
taka, że
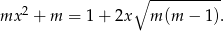
Suma pierwiastków trójmianu 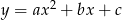 jest równa
jest równa 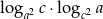 , gdzie
, gdzie 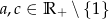 . Uzasadnij, że odcięta wierzchołka paraboli będącej wykresem tego trójmianu jest równa
. Uzasadnij, że odcięta wierzchołka paraboli będącej wykresem tego trójmianu jest równa  .
.
