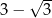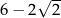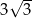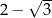Odcinek 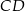 jest wysokością trójkąta
jest wysokością trójkąta 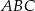 , w którym
, w którym 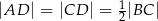 (zobacz rysunek). Okrąg o środku
(zobacz rysunek). Okrąg o środku 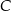 i promieniu
i promieniu 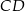 jest styczny do prostej
jest styczny do prostej 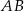 . Okrąg ten przecina boki
. Okrąg ten przecina boki 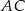 i
i 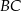 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 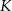 i
i 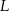 .
.
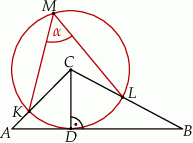
Zaznaczony na rysunku kąt  wpisany w okrąg jest równy
wpisany w okrąg jest równy
A) 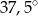 B)
B) 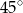 C)
C) 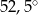 D)
D) 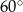

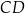 jest wysokością trójkąta równoramiennego
jest wysokością trójkąta równoramiennego 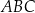 , w którym
, w którym 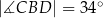 (zobacz rysunek). Okrąg o środku
(zobacz rysunek). Okrąg o środku 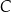 i promieniu
i promieniu 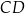 jest styczny do prostej
jest styczny do prostej 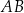 . Okrąg ten przecina boki
. Okrąg ten przecina boki 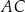 i
i 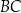 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 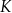 i
i 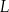 .
. 
 wpisany w okrąg jest równy
wpisany w okrąg jest równy 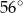
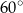
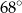
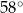
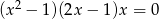 nie jest liczba
nie jest liczba 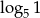
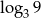
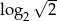
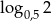
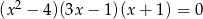 nie jest liczba
nie jest liczba 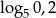
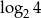
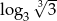
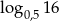
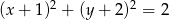 :
: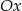 ,
, 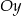 ,
, 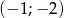 .
. 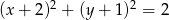 :
: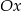 ,
, 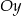 ,
, 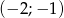 .
. 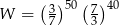 jest równe
jest równe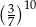
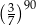
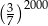
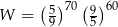 jest równe
jest równe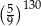
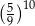
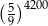
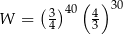 jest równe
jest równe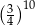
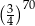
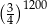
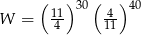 jest równe
jest równe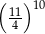
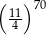
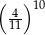
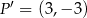 jest obrazem punktu
jest obrazem punktu 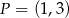 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 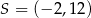 . Skala tej jednokładności jest równa
. Skala tej jednokładności jest równa 

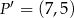 jest obrazem punktu
jest obrazem punktu 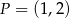 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 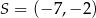 . Skala tej jednokładności jest równa
. Skala tej jednokładności jest równa 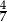

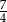
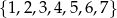 losujemy kolejno bez zwracania dwie cyfry i zapisujemy je, tworząc liczbę dwucyfrową. Ile jest możliwości utworzenia w ten sposób liczby podzielnej przez 3?
losujemy kolejno bez zwracania dwie cyfry i zapisujemy je, tworząc liczbę dwucyfrową. Ile jest możliwości utworzenia w ten sposób liczby podzielnej przez 3?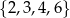 losujemy kolejno ze zwracaniem trzy cyfry i zapisujemy je, tworząc liczbę trzycyfrową. Ile jest możliwości utworzenia w ten sposób liczby podzielnej przez 3?
losujemy kolejno ze zwracaniem trzy cyfry i zapisujemy je, tworząc liczbę trzycyfrową. Ile jest możliwości utworzenia w ten sposób liczby podzielnej przez 3?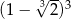 jest równa
jest równa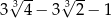
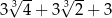
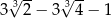
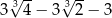
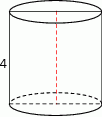
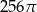
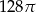
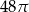
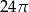
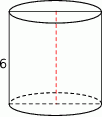
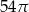
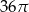
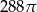
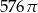
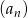 pierwszy wyraz jest równy
pierwszy wyraz jest równy 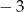 , zaś
, zaś 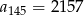 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba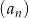 pierwszy wyraz jest równy 45, zaś
pierwszy wyraz jest równy 45, zaś 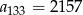 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba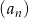 pierwszy wyraz jest równy 32, zaś
pierwszy wyraz jest równy 32, zaś 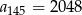 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba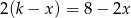 z niewiadomą
z niewiadomą  ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla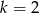
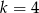
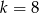
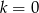
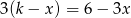 z niewiadomą
z niewiadomą  ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla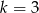
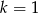
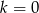
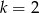
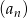 o wyrazie ogólnym
o wyrazie ogólnym 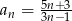 jest równy 2?
jest równy 2? 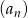 o wyrazie ogólnym
o wyrazie ogólnym 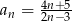 jest równy 3?
jest równy 3? 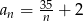 . Wartość
. Wartość  ma wyraz
ma wyraz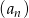 określony jest wzorem
określony jest wzorem 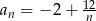 dla
dla 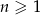 . Równość
. Równość 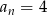 zachodzi dla
zachodzi dla 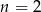
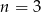
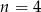
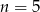
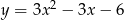 .
. 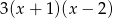
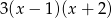
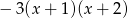
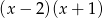
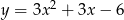 .
. 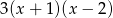
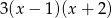
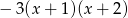
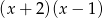
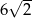 kąt rozwarty ma miarę
kąt rozwarty ma miarę 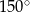 . Iloczyn długości przekątnych tego rombu jest równy
. Iloczyn długości przekątnych tego rombu jest równy 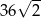
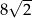 kąt rozwarty ma miarę
kąt rozwarty ma miarę 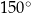 . Iloczyn długości przekątnych tego rombu jest równy
. Iloczyn długości przekątnych tego rombu jest równy 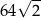
 . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe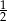
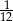
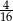

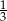
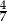 . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe

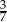
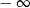
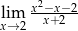
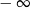
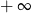
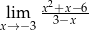
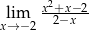
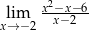
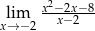
 jest rozwarty i
jest rozwarty i 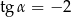 . Wobec tego
. Wobec tego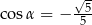
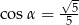
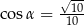
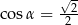
 jest rozwarty i
jest rozwarty i 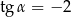 . Wobec tego
. Wobec tego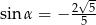
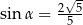
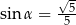
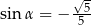
 jest rozwarty i
jest rozwarty i 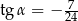 . Wobec tego
. Wobec tego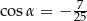
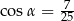
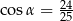
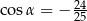
 jest rozwarty i
jest rozwarty i 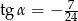 . Wobec tego
. Wobec tego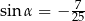
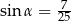
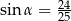
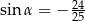
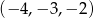
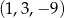
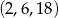
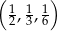
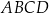 jest równe
jest równe 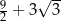 . Ponadto:
. Ponadto: 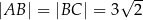 ,
, 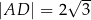 ,
, 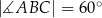 ,
, 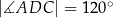 (zobacz rysunek).
(zobacz rysunek). 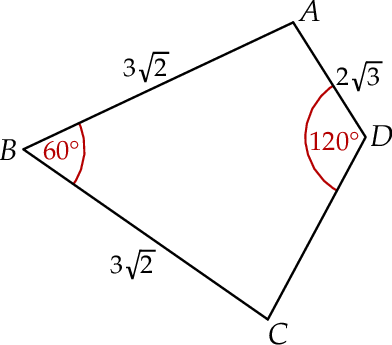
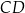 jest równa
jest równa