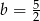Stosunek miar kątów czworokąta jest równy 1:2:3:4. Zatem najmniejszy kąt tego wielokąta ma miarę
A) 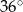 B)
B) 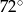 C)
C) 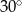 D)
D) 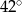
/Szkoła średnia/Zadania testowe
Stosunek miar kątów czworokąta jest równy 6:7:8:9. Najmniejszy kąt tego czworokąta ma miarę
A) 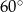 B)
B) 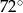 C)
C) 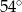 D)
D) 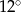
Stosunek miar kątów czworokąta jest równy 1:2:3:4. Zatem największy kąt tego wielokąta ma miarę
A) 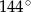 B)
B) 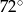 C)
C) 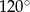 D)
D) 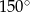
Miary kątów pewnego czworokąta pozostają w stosunku 2:3:3:4. Wynika stąd, że najmniejszy kąt tego czworokąta ma miarę
A) 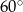 B)
B) 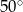 C)
C) 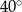 D)
D) 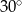
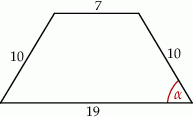
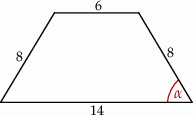
Dany jest trapez równoramienny (patrz rysunek). Wtedy 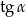 jest równy
jest równy
A) 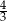 B)
B)  C)
C)  D)
D) 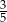
Dany jest trapez równoramienny (patrz rysunek). Wtedy 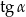 jest równy
jest równy
A) 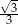 B)
B) 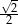 C)
C) 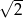 D)
D) 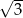
Liczby 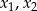 są rozwiązaniami równania
są rozwiązaniami równania 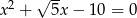 . Liczba
. Liczba 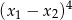 jest równa
jest równa
A) 45 B) 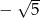 C) 2025 D) 10
C) 2025 D) 10
Wykres funkcji 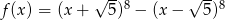 przecina oś
przecina oś 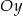 w punkcie
w punkcie
A) 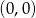 B)
B) 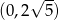 C)
C) 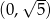 D)
D) 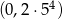
Wykres funkcji 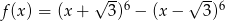 przecina oś
przecina oś 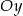 w punkcie
w punkcie
A) 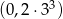 B)
B) 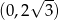 C)
C) 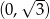 D)
D) 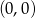
Wykres funkcji 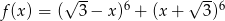 przecina oś
przecina oś 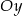 w punkcie
w punkcie
A) 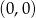 B)
B) 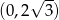 C)
C) 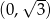 D)
D) 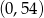
Ile wyrazów równych zero ma nieskończony ciąg 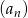 o wyrazie ogólnym
o wyrazie ogólnym
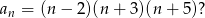
A) 0 B) 1 C) 2 D) 3
Ile wyrazów równych zero ma nieskończony ciąg 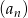 o wyrazie ogólnym
o wyrazie ogólnym
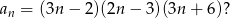
A) 0 B) 1 C) 2 D) 3
Ile wyrazów równych zero ma nieskończony ciąg 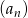 o wyrazie ogólnym
o wyrazie ogólnym
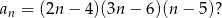
A) 0 B) 1 C) 2 D) 3
Wyrażenie 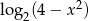 jest określone dla wszystkich liczb
jest określone dla wszystkich liczb  spełniających warunek
spełniających warunek
A) 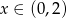 B)
B) 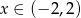 C)
C) 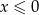 D)
D) 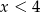
Wyrażenie 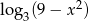 jest określone dla wszystkich liczb
jest określone dla wszystkich liczb  spełniających warunek
spełniających warunek
A) 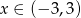 B)
B) 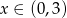 C)
C) 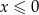 D)
D) 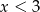
Obwód podstawy ostrosłupa prawidłowego siedmiokątnego jest równy 33,6 cm, a długość jego krawędzi bocznej jest równa 2,5 cm. Pole powierzchni bocznej tego ostrosłupa jest równe
A) 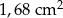 B)
B) 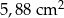 C)
C) 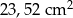 D)
D) 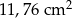
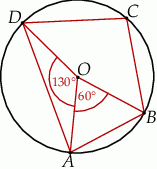
Punkt 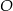 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
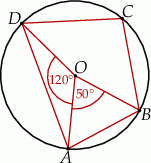
A) 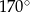 B)
B) 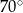 C)
C) 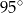 D)
D) 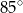
Punkt  jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
A) 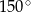 B)
B) 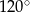 C)
C) 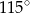 D)
D) 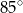
Dany jest trójkąt 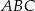 , w którym
, w którym 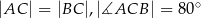 , zaś
, zaś 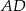 jest dwusieczną kąta
jest dwusieczną kąta 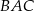 i
i 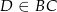 . Wówczas miara kąta
. Wówczas miara kąta 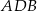 jest równa
jest równa
A) 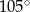 B)
B) 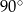 C)
C) 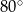 D)
D) 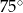
Dany jest trójkąt równoramienny 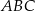 . Kąt
. Kąt 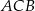 ma miarę
ma miarę 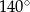 , a dwusieczna kąta
, a dwusieczna kąta 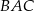 przecina bok
przecina bok 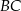 w punkcie
w punkcie 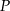 . Miara kąta
. Miara kąta 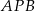 jest równa
jest równa
A) 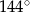 B)
B) 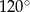 C)
C) 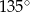 D)
D) 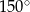
Dany jest trójkąt 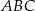 , w którym
, w którym 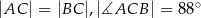 , zaś
, zaś 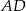 jest dwusieczną kąta
jest dwusieczną kąta 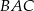 i
i 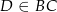 . Wówczas miara kąta
. Wówczas miara kąta 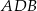 jest równa
jest równa
A) 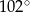 B)
B) 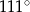 C)
C) 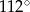 D)
D) 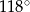
Dany jest trójkąt równoramienny 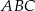 , w którym
, w którym 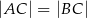 . Kąt między ramionami tego trójkąta ma miarę
. Kąt między ramionami tego trójkąta ma miarę 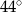 . Dwusieczna kąta poprowadzona z wierzchołka
. Dwusieczna kąta poprowadzona z wierzchołka 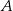 przecina bok
przecina bok 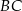 tego trójkąta w punkcie
tego trójkąta w punkcie 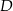 . Kąt
. Kąt 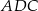 ma miarę
ma miarę
A) 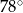 B)
B) 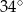 C)
C) 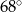 D)
D) 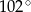
Dany jest trójkąt 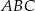 , w którym
, w którym 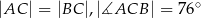 , zaś
, zaś 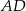 jest dwusieczną kąta
jest dwusieczną kąta 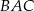 i
i 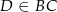 . Wówczas miara kąta
. Wówczas miara kąta 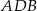 jest równa
jest równa
A) 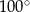 B)
B) 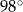 C)
C) 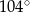 D)
D) 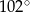
Dany jest trójkąt równoramienny 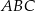 . Kąt
. Kąt 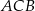 ma miarę
ma miarę 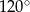 , a dwusieczna kąta
, a dwusieczna kąta 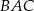 przecina bok
przecina bok 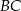 w punkcie
w punkcie 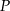 . Miara kąta
. Miara kąta 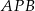 jest równa
jest równa
A) 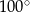 B)
B) 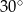 C)
C) 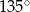 D)
D) 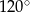
Rozwiązaniem równania 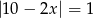 są liczby
są liczby
A) przeciwne B) różniące się o 1 C) całkowite D) niewymierne
Rozwiązaniem równania 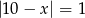 są liczby
są liczby
A) przeciwne B) różniące się o 1 C) całkowite D) niewymierne
Rozwiązaniem równania 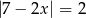 są liczby
są liczby
A) przeciwne B) różniące się o 1 C) całkowite D) różniące się o 2
Narysowana bryła ma w podstawie kwadrat, a krawędzie boczne są prostopadłe do podstawy. Objętość tej bryły jest równa
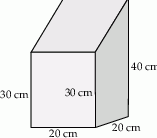
A) 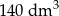 B)
B) 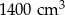 C)
C) 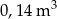 D)
D) 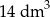
Wskaż 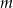 , dla którego funkcja liniowa
, dla którego funkcja liniowa 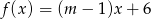 jest rosnąca
jest rosnąca
A) 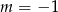 B)
B) 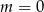 C)
C) 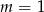 D)
D) 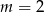
Wskaż 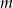 , dla którego funkcja liniowa
, dla którego funkcja liniowa 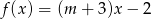 jest malejąca
jest malejąca
A) 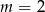 B)
B) 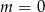 C)
C) 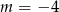 D)
D) 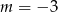
Promień okręgu o równaniu 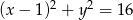 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Promień okręgu o równaniu 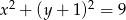 jest równy
jest równy
A) 1 B) 2 C) 3 D) 9
Promień okręgu o równaniu 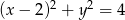 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Promień okręgu o równaniu 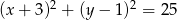 jest równy
jest równy
A) 25 B) 5 C) 625 D) 15
Promień okręgu o równaniu 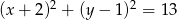 jest równy
jest równy
A) 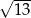 B) 13 C) 8 D)
B) 13 C) 8 D) 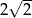
Promień okręgu o równaniu 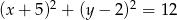 jest równy
jest równy
A) 12 B) 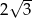 C)
C) 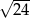 D) 144
D) 144
W szufladzie jest 40 koszulek, wśród których 10% jest zielonych, a pozostałe są niebieskie. Losowo wyciągamy po jednej koszulce i - bez oglądania - odkładamy do pudełka. Ile co najmniej koszulek należy wyciągnąć, aby mieć pewność, że w pudełku będą co najmniej trzy koszulki niebieskie?
A) 20 B) 10 C) 7 D) 3
W szufladzie jest 50 koszulek, wśród których 30% jest zielonych, a pozostałe są niebieskie. Losowo wyciągamy po jednej koszulce i - bez oglądania - odkładamy do pudełka. Ile co najmniej koszulek należy teraz wyciągnąć, aby mieć pewność, że w pudełku będzie co najmniej pięć koszulek niebieskich?
A) 20 B) 10 C) 7 D) 3
W szufladzie jest 35 koszulek, wśród których 20% jest zielonych, a pozostałe są niebieskie. Losowo wyciągamy po jednej koszulce i - bez oglądania - odkładamy do pudełka. Ile co najmniej koszulek należy teraz wyciągnąć, aby mieć pewność, że w pudełku będą co najmniej trzy koszulki niebieskie?
A) 20 B) 10 C) 7 D) 3
Dany jest trójkąt 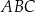 , w którym
, w którym 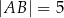 ,
, 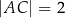 oraz
oraz 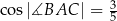 . Długość boku
. Długość boku 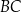 tego trójkąta jest równa
tego trójkąta jest równa
A) 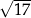 B)
B) 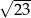 C)
C) 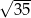 D)
D) 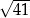
Ile miejsc zerowych ma funkcja 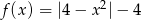 ?
?
A) 1 B) 2 C) 3 D) 4
Dany jest trapez prostokątny  , w którym
, w którym 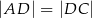 oraz
oraz 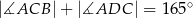 (zobacz rysunek).
(zobacz rysunek).
Stąd wynika, że
A)  B)
B)  C)
C) 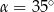 D)
D) 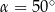
Na rysunku jest przedstawiony wykres funkcji 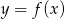 .
.
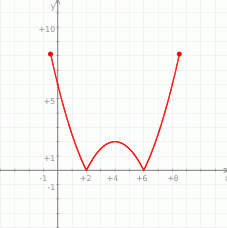
Które równanie ma dokładnie trzy rozwiązania?
A) 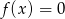 B)
B) 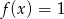 C)
C) 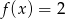 D)
D) 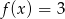
Na rysunku jest przedstawiony wykres funkcji 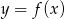 .
.
Które równanie ma dokładnie trzy rozwiązania?
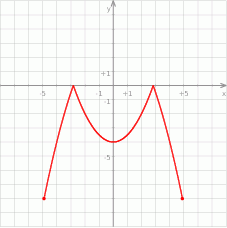
A) 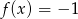 B)
B)  C)
C) 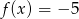 D)
D) 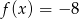
Na rysunku jest przedstawiony wykres funkcji 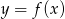 .
.
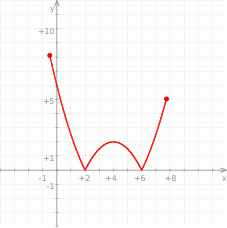
Które równanie ma dokładnie jedno rozwiązanie?
A) 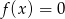 B)
B) 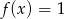 C)
C) 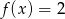 D)
D) 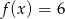
Punkty 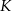 i
i 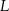 są punktami styczności okręgu wpisanego w trapez równoramienny
są punktami styczności okręgu wpisanego w trapez równoramienny 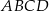 z bokami
z bokami 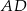 i
i 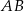 . Kąt ostry tego trapezu ma miarę
. Kąt ostry tego trapezu ma miarę 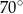 (zobacz rysunek).
(zobacz rysunek).
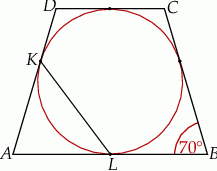
Miara kąta 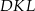 jest równa
jest równa
A) 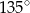 B)
B) 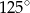 C)
C) 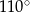 D)
D) 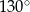
Punkt 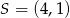 jest środkiem odcinka
jest środkiem odcinka 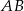 , gdzie
, gdzie 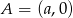 i
i 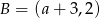 . Wówczas
. Wówczas
A) 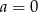 B)
B) 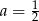 C)
C) 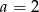 D)
D) 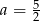
Punkt 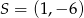 jest środkiem odcinka
jest środkiem odcinka 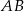 , gdzie
, gdzie 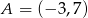 i
i 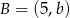 . Wtedy
. Wtedy
A) 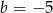 B)
B) 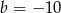 C)
C) 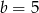 D)
D) 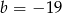
Punkt 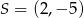 jest środkiem odcinka
jest środkiem odcinka 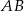 , gdzie
, gdzie 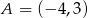 i
i 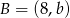 . Wtedy
. Wtedy
A) 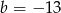 B)
B) 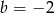 C)
C) 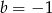 D)
D) 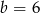
Punkt 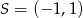 jest środkiem odcinka
jest środkiem odcinka 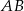 , gdzie
, gdzie 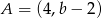 i
i 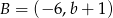 . Wówczas
. Wówczas
A) 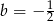 B)
B) 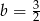 C)
C) 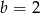 D)
D)