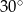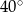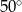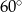Odcinek 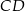 jest wysokością trójkąta
jest wysokością trójkąta 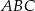 , w którym
, w którym 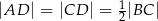 (zobacz rysunek). Okrąg o środku
(zobacz rysunek). Okrąg o środku 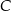 i promieniu
i promieniu 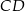 jest styczny do prostej
jest styczny do prostej 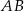 . Okrąg ten przecina boki
. Okrąg ten przecina boki 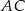 i
i 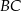 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 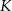 i
i 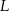 .
.
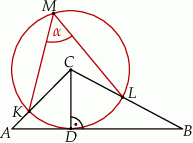
Zaznaczony na rysunku kąt  wpisany w okrąg jest równy
wpisany w okrąg jest równy
A) 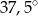 B)
B) 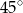 C)
C) 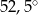 D)
D) 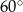

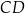 jest wysokością trójkąta równoramiennego
jest wysokością trójkąta równoramiennego 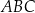 , w którym
, w którym 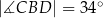 (zobacz rysunek). Okrąg o środku
(zobacz rysunek). Okrąg o środku 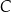 i promieniu
i promieniu 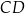 jest styczny do prostej
jest styczny do prostej 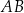 . Okrąg ten przecina boki
. Okrąg ten przecina boki 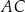 i
i 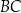 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 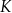 i
i 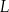 .
. 
 wpisany w okrąg jest równy
wpisany w okrąg jest równy 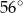
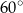
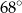
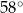
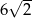 kąt rozwarty ma miarę
kąt rozwarty ma miarę 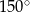 . Iloczyn długości przekątnych tego rombu jest równy
. Iloczyn długości przekątnych tego rombu jest równy 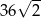
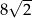 kąt rozwarty ma miarę
kąt rozwarty ma miarę 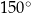 . Iloczyn długości przekątnych tego rombu jest równy
. Iloczyn długości przekątnych tego rombu jest równy 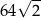
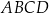 jest równe
jest równe 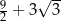 . Ponadto:
. Ponadto: 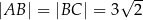 ,
, 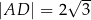 ,
, 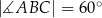 ,
, 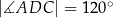 (zobacz rysunek).
(zobacz rysunek). 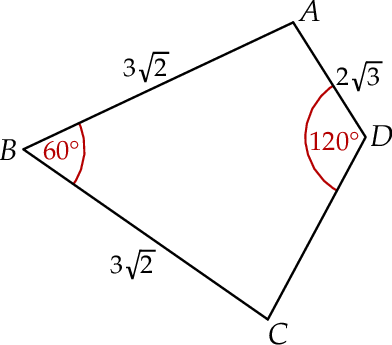
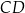 jest równa
jest równa 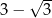
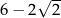
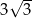
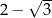
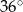
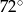
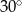
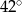
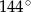
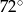
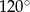
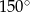
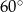
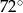
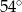
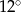
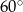
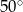
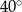
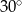
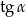 jest równy
jest równy 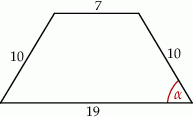
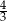


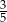
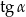 jest równy
jest równy 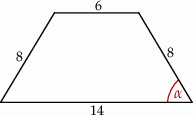
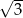
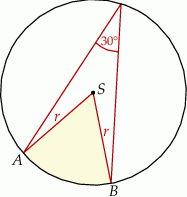
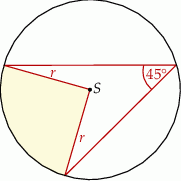
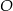 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany 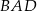 ma miarę
ma miarę 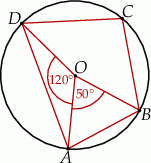
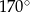
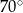
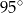
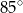
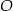 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany 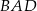 ma miarę
ma miarę 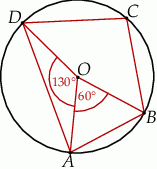
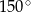
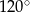
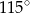
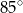
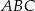 , w którym
, w którym 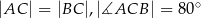 , zaś
, zaś 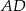 jest dwusieczną kąta
jest dwusieczną kąta 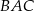 i
i 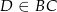 . Wówczas miara kąta
. Wówczas miara kąta 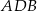 jest równa
jest równa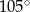
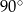
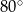
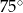
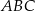 . Kąt
. Kąt 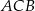 ma miarę
ma miarę 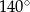 , a dwusieczna kąta
, a dwusieczna kąta 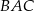 przecina bok
przecina bok 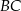 w punkcie
w punkcie 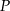 . Miara kąta
. Miara kąta 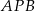 jest równa
jest równa 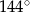
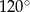
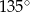
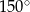
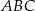 , w którym
, w którym 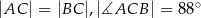 , zaś
, zaś 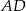 jest dwusieczną kąta
jest dwusieczną kąta 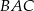 i
i 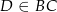 . Wówczas miara kąta
. Wówczas miara kąta 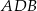 jest równa
jest równa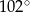
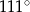
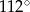
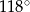
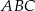 , w którym
, w którym 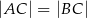 . Kąt między ramionami tego trójkąta ma miarę
. Kąt między ramionami tego trójkąta ma miarę 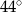 . Dwusieczna kąta poprowadzona z wierzchołka
. Dwusieczna kąta poprowadzona z wierzchołka 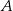 przecina bok
przecina bok 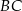 tego trójkąta w punkcie
tego trójkąta w punkcie 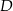 . Kąt
. Kąt 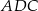 ma miarę
ma miarę 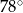
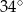
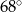
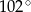
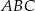 , w którym
, w którym 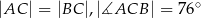 , zaś
, zaś 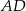 jest dwusieczną kąta
jest dwusieczną kąta 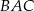 i
i 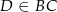 . Wówczas miara kąta
. Wówczas miara kąta 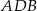 jest równa
jest równa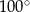
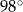
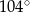
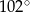
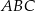 . Kąt
. Kąt 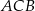 ma miarę
ma miarę 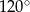 , a dwusieczna kąta
, a dwusieczna kąta 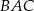 przecina bok
przecina bok 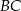 w punkcie
w punkcie 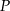 . Miara kąta
. Miara kąta 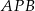 jest równa
jest równa 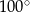
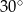
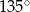
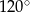
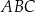 , w którym
, w którym 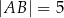 ,
, 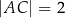 oraz
oraz 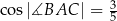 . Długość boku
. Długość boku 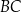 tego trójkąta jest równa
tego trójkąta jest równa 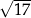
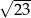
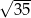
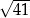
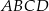 , w którym
, w którym 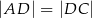 oraz
oraz 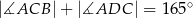 (zobacz rysunek).
(zobacz rysunek). 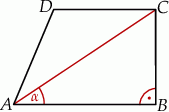
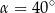
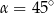
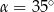
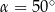
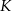 i
i 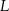 są punktami styczności okręgu wpisanego w trapez równoramienny
są punktami styczności okręgu wpisanego w trapez równoramienny 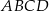 z bokami
z bokami 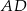 i
i 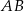 . Kąt ostry tego trapezu ma miarę
. Kąt ostry tego trapezu ma miarę 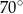 (zobacz rysunek).
(zobacz rysunek). 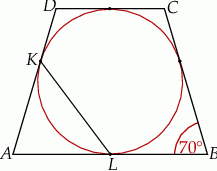
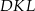 jest równa
jest równa 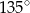
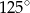
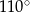
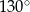
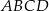 o podstawach
o podstawach 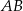 i
i 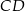 dane są:
dane są: 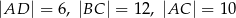 oraz
oraz 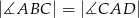 (zobacz rysunek).
(zobacz rysunek). 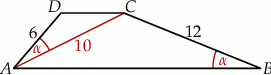
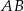 tego trapezu jest równa
tego trapezu jest równa 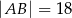
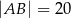
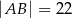
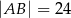
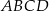 o podstawach
o podstawach 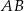 i
i 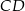 dane są:
dane są: 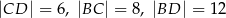 oraz
oraz 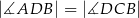 (zobacz rysunek).
(zobacz rysunek). 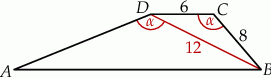
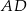 tego trapezu jest równa
tego trapezu jest równa 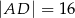
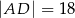
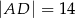
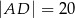
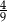 długości okręgu, ma miarę
długości okręgu, ma miarę 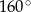
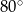
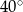
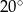
 długości okręgu, ma miarę
długości okręgu, ma miarę 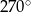
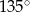
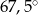
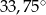
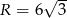 jest równe
jest równe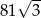
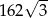
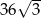
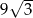
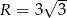 jest równe
jest równe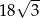
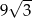
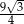
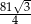
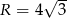 jest równe
jest równe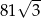
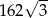
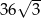
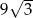
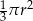
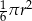
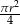
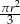
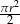
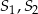 i promieniach odpowiednio równych
i promieniach odpowiednio równych 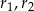 . Jeśli
. Jeśli 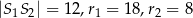 , to okręgi
, to okręgi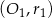 i
i 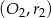 jeżeli wiadomo, że:
jeżeli wiadomo, że: 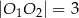 ,
, 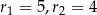
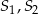 i promieniach odpowiednio równych
i promieniach odpowiednio równych 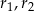 . Jeśli
. Jeśli 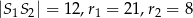 , to okręgi
, to okręgi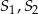 i promieniach odpowiednio równych
i promieniach odpowiednio równych 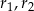 . Jeśli
. Jeśli 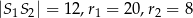 , to okręgi
, to okręgi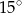 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe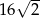
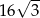
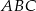 mają długości 12 cm, 15 cm, 18 cm. Trójkąt
mają długości 12 cm, 15 cm, 18 cm. Trójkąt 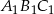 jest podobny do trójkąta
jest podobny do trójkąta 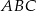 . Najdłuższy bok trójkąta
. Najdłuższy bok trójkąta 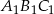 ma długość 6 cm. Obwód trójkąta
ma długość 6 cm. Obwód trójkąta 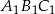 jest równy
jest równy 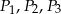 . Wówczas
. Wówczas 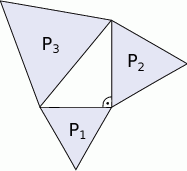
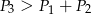
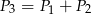
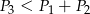
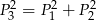
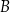 i
i 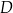 trapezu
trapezu 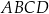 są równe odpowiednio
są równe odpowiednio 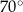 i
i 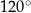 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 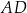 i
i 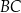 przecinają się pod kątem
przecinają się pod kątem 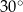
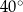
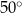
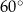
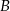 i
i 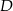 trapezu
trapezu 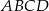 są równe odpowiednio
są równe odpowiednio 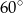 i
i 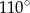 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 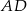 i
i 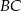 przecinają się pod kątem
przecinają się pod kątem