Pole trójkąta 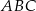 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
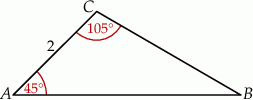
A) 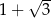 B)
B) 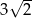 C)
C) 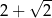 D)
D) 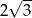
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Pole trójkąta 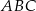 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe

A) 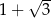 B)
B) 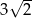 C)
C) 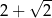 D)
D) 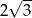
W trójkącie prostokątnym środkowa poprowadzona na przeciwprostokątną ma długość 4. Pole koła opisanego na tym trójkącie wynosi
A) 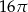 B)
B) 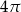 C)
C) 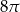 D)
D) 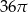
Środkowa w trójkącie prostokątnym poprowadzona z wierzchołka kąta prostego ma długość 1. Zatem pole koła opisanego na tym trójkącie wynosi
A) 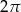 B)
B) 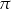 C)
C) 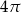 D)
D) 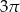
Kąty między bokiem trójkąta ostrokątnego a wysokościami opuszczonymi z należących do tego boku wierzchołków mają miary 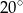 i
i 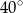 . Kąty tego trójkąta mają miary:
. Kąty tego trójkąta mają miary:
A) 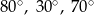 B)
B) 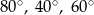 C)
C) 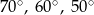 D)
D) 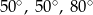
Kąty między bokiem trójkąta ostrokątnego a wysokościami opuszczonymi z należących do tego boku wierzchołków mają miary 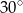 i
i 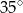 . Kąty tego trójkąta mają miary:
. Kąty tego trójkąta mają miary:
A) 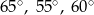 B)
B) 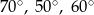 C)
C) 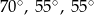 D)
D) 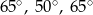
Jeśli przyprostokątne trójkąta prostokątnego są równe 6 i 3, a najmniejszy kąt ma miarę  , to wyrażenie
, to wyrażenie 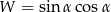 ma wartość
ma wartość
A) 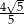 B)
B) 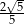 C)
C)  D)
D) 
W trójkącie prostokątnym o przyprostokątnych długości 1 i 2 kąty ostre są równe  i
i 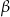 (
(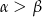 ). Wartość wyrażenia
). Wartość wyrażenia 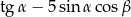 jest równe
jest równe
A) 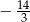 B) -2 C) 0 D)
B) -2 C) 0 D) 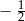
Dany jest trójkąt o bokach długości 4, 5 oraz 6. Cosinus największego kąta wewnętrznego tego trójkąta jest równy
A) 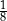 B)
B) 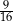 C)
C)  D)
D) 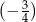
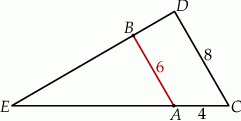
Oblicz długość odcinka 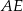 wiedząc, że
wiedząc, że 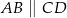 i
i 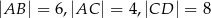 .
.
A) 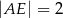 B)
B) 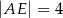 C)
C) 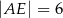 D)
D) 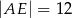
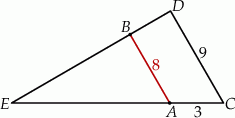
Oblicz długość odcinka 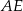 wiedząc, że
wiedząc, że 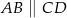 i
i 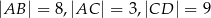 .
.
A) 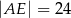 B)
B) 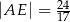 C)
C) 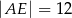 D)
D) 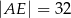
W trójkącie 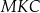 bok
bok 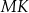 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 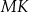 przecina boki
przecina boki 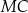 i
i 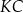 – odpowiednio – w punktach
– odpowiednio – w punktach 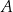 oraz
oraz 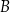 takich, że
takich, że 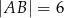 i
i 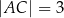 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 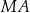 jest równa
jest równa
A) 18 B) 15 C) 9 D) 12
Oblicz długość odcinka 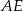 wiedząc, że
wiedząc, że 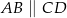 i
i 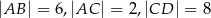 .
.
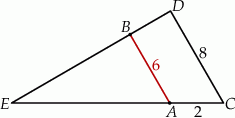
A) 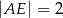 B)
B) 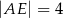 C)
C) 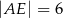 D)
D) 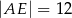
W trójkącie 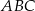 punkt
punkt 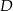 leży na boku
leży na boku 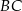 , a punkt
, a punkt 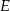 leży na boku
leży na boku 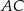 . Odcinek
. Odcinek 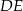 jest równoległy do boku
jest równoległy do boku 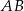 , a ponadto
, a ponadto 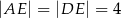 ,
, 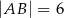 (zobacz rysunek).
(zobacz rysunek).
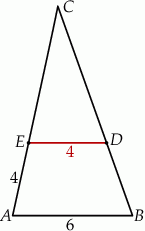
Odcinek 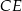 ma długość
ma długość
A) 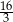 B)
B)  C) 8 D) 6
C) 8 D) 6
W trójkącie 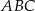 punkt
punkt 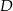 leży na boku
leży na boku 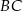 , a punkt
, a punkt 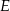 leży na boku
leży na boku 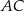 . Odcinek
. Odcinek 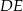 jest równoległy do boku
jest równoległy do boku 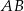 , a ponadto
, a ponadto 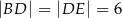 ,
, 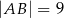 (zobacz rysunek).
(zobacz rysunek).
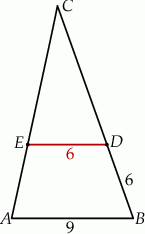
Odcinek 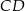 ma długość
ma długość
A) 8 B) 4 C) 9 D) 12
Oblicz długość odcinka 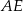 wiedząc, że
wiedząc, że 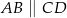 i
i 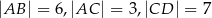 .
.
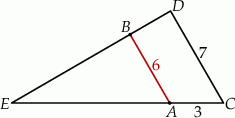
A) 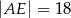 B)
B) 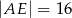 C)
C) 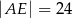 D)
D) 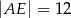
Jeżeli odcinki 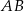 i
i 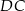 są równoległe, to długość odcinka
są równoległe, to długość odcinka 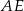 (patrz rys.) jest równa
(patrz rys.) jest równa
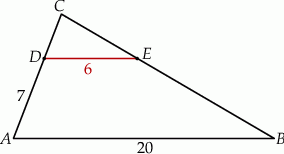
A) 9 B) 10 C) 11 D) 12
Odcinki 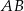 i
i 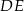 są równoległe. Długości odcinków
są równoległe. Długości odcinków 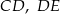 i
i 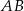 są odpowiednio równe 2, 5 i 15.
są odpowiednio równe 2, 5 i 15.
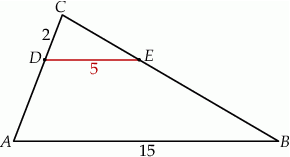
Długość odcinka 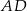 jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Odcinki 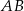 i
i 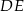 są równoległe. Długości odcinków
są równoległe. Długości odcinków 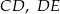 i
i 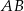 są odpowiednio równe 2, 4 i 16.
są odpowiednio równe 2, 4 i 16.
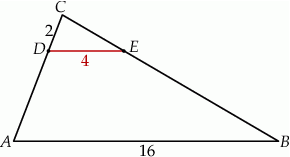
Długość odcinka 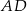 jest równa
jest równa
A) 12 B) 8 C) 3 D) 6
Odcinki 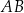 i
i 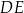 są równoległe. Długości odcinków
są równoległe. Długości odcinków 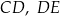 i
i 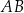 są odpowiednio równe 1, 3 i 9.
są odpowiednio równe 1, 3 i 9.
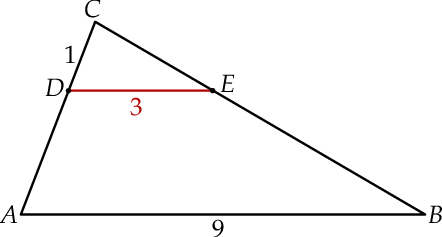
Długość odcinka 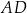 jest równa
jest równa
A) 2 B) 3 C) 5 D) 6
W trójkącie równoramiennym miara kąta przy podstawie jest równa 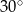 , a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
, a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
A) 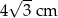 B) 4 cm C)
B) 4 cm C) 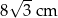 D)
D) 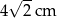
Ramię trójkąta równoramiennego ma długość 12 i tworzy z podstawą kąt o mierze 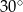 . Obwód tego trójkąta jest równy:
. Obwód tego trójkąta jest równy:
A) 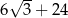 B) 30 C) 36 D)
B) 30 C) 36 D) 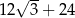
Punkt 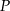 jest punktem wspólnym środkowych
jest punktem wspólnym środkowych 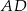 i
i 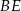 w trójkącie
w trójkącie 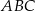 . Wówczas odcinki
. Wówczas odcinki 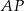 i
i 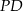 mogą mieć długości
mogą mieć długości
A) 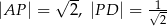 B)
B) 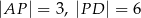
C) 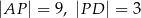 D)
D) 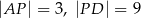
Dany jest trójkąt równoboczny, którego pole jest równe 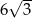 . Bok tego trójkąta ma długość
. Bok tego trójkąta ma długość
A) 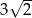 B)
B) 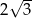 C)
C) 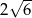 D)
D) 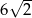
Pole pewnego trójkąta równobocznego jest równe 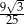 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 4 B) 2 C) 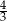 D)
D) 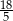
Dany jest trójkąt równoboczny, którego pole jest równe 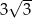 . Bok tego trójkąta ma długość
. Bok tego trójkąta ma długość
A) 3 B) 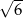 C) 6 D)
C) 6 D) 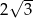
Pole pewnego trójkąta równobocznego jest równe 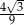 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 4 B) 2 C) 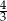 D)
D) 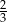
W trójkącie zwiększono długość każdego boku o 20%. O ile procent wzrosło pole tego trójkąta?
A) 20% B) 40% C) 44% D) 400%
Pole trójkąta 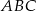 wynosi
wynosi 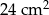 . Połączono środki boków tego trójkąta i otrzymano trójkąt
. Połączono środki boków tego trójkąta i otrzymano trójkąt 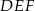 , którego pole jest równe
, którego pole jest równe
A) 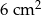 B)
B) 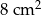 C)
C) 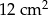 D)
D) 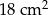
W trójkącie prostokątnym 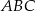 odcinek
odcinek 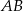 jest przeciwprostokątną i
jest przeciwprostokątną i 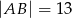 oraz
oraz 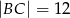 . Wówczas sinus kąta
. Wówczas sinus kąta 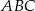 jest równy
jest równy
A) 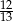 B)
B) 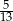 C)
C) 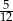 D)
D) 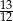
W trójkącie prostokątnym 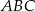 odcinek
odcinek 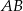 jest przeciwprostokątną i
jest przeciwprostokątną i 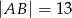 oraz
oraz 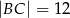 . Wówczas tangens kąta
. Wówczas tangens kąta 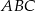 jest równy
jest równy
A) 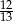 B)
B) 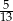 C)
C) 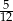 D)
D) 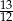
Sinusy dwóch kątów ostrych trójkąta są odpowiednio równe 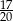 i
i 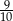 . Jeżeli
. Jeżeli  jest miarą najmniejszego kąta tego trójkąta, to
jest miarą najmniejszego kąta tego trójkąta, to
A) 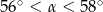 B)
B) 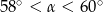 C)
C) 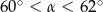 D)
D) 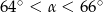
Przyprostokątna trójkąta prostokątnego ma długość 6, a przeciwprostokątna ma długość 8. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 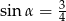 B)
B) 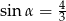 C)
C) 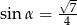 D)
D) 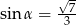
Przyprostokątna trójkąta prostokątnego ma długość 7, a przeciwprostokątna ma długość 9. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 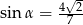 B)
B) 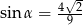 C)
C) 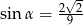 D)
D) 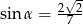
Przyprostokątna trójkąta prostokątnego ma długość 6, a przeciwprostokątna ma długość 8. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 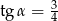 B)
B) 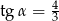 C)
C) 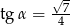 D)
D) 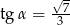
Pole trójkąta równobocznego o obwodzie 6 jest równe
A) 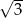 B)
B) 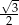 C)
C) 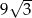 D)
D) 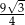
W trójkącie prostokątnym 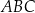 sinus kąta
sinus kąta 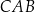 jest równy
jest równy  , a przeciwprostokątna
, a przeciwprostokątna 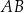 jest o 8 dłuższa od przyprostokątnej
jest o 8 dłuższa od przyprostokątnej 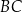 . Długość przeciwprostokątnej
. Długość przeciwprostokątnej 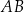 tego trójkąta jest równa
tego trójkąta jest równa
A) 18 B) 20 C) 24 D) 25
Dany jest trójkąt równoramienny 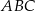 , w którym
, w którym 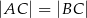 . Na podstawie
. Na podstawie 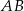 tego trójkąta leży punkt
tego trójkąta leży punkt 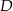 , taki że
, taki że 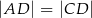 ,
, 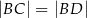 (zobacz rysunek).
(zobacz rysunek).
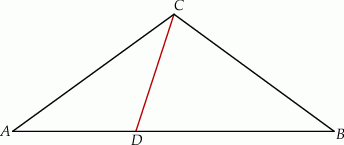
Wynika stąd, że kąt 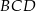 ma miarę
ma miarę
A) 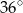 B)
B) 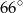 C)
C) 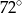 D)
D) 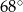
W trójkącie równoramiennym ramię ma długość 5, a kąt ostry przy podstawie jest równy  . Wysokość poprowadzona na podstawę trójkąta wynosi
. Wysokość poprowadzona na podstawę trójkąta wynosi
A) 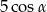 B)
B) 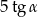 C)
C) 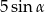 D)
D) 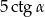
Przeciwprostokątna 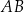 trójkąta prostokątnego
trójkąta prostokątnego 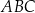 ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
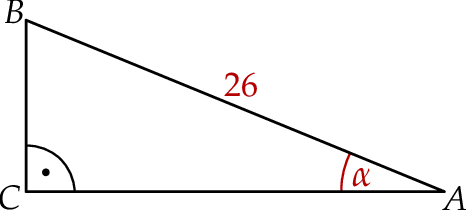
Jeżeli  jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia
jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia 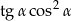 jest równa
jest równa
A) 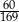 B)
B) 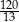 C)
C) 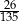 D)
D) 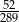
Znajdź skalę podobieństwa trójkąta 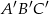 do trójkąta
do trójkąta 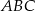 :
:
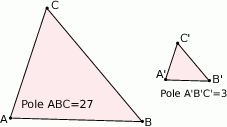
A) 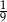 B)
B) 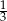 C) 3 D) 9
C) 3 D) 9
Znajdź skalę podobieństwa trójkąta 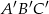 do trójkąta
do trójkąta 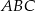 :
:
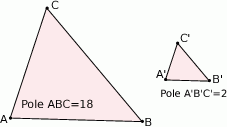
A) 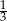 B)
B) 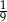 C) 3 D) 9
C) 3 D) 9
