Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 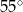 i
i 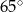 ?
?
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 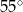 i
i 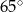 ?
?

Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 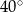 i
i 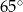 ?
?
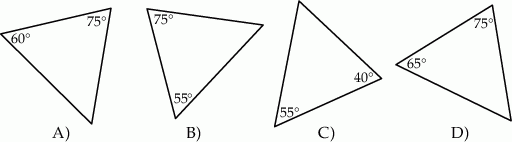
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 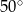 i
i 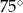 ?
?
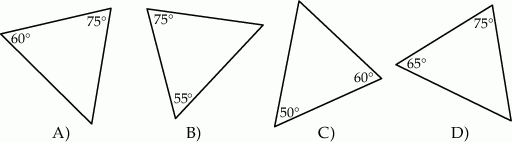
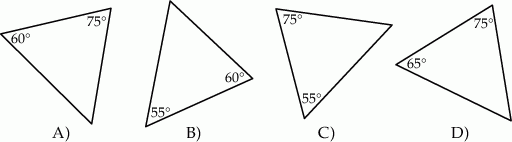
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 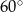 i
i 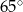 ?
?
Wysokość trójkąta równobocznego jest o 2 krótsza od boku tego trójkąta. Bok trójkąta ma długość
A) 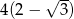 B)
B) 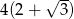 C)
C) 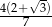 D)
D) 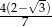
Wysokość trójkąta równobocznego jest o 4 krótsza od boku tego trójkąta. Bok trójkąta ma długość
A) 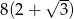 B)
B) 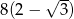 C)
C) 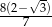 D)
D) 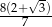
Wysokość trójkąta równobocznego jest o 3 krótsza od boku tego trójkąta. Bok trójkąta jest ma długość
A) 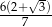 B)
B) 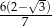 C)
C) 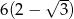 D)
D) 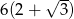
Obwód trójkąta 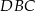 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
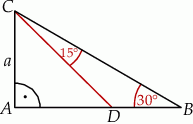
A) 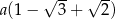 B)
B) 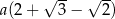 C)
C) 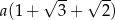 D)
D) 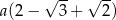
Punkty 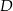 i
i 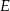 są środkami przyprostokątnych
są środkami przyprostokątnych 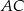 i
i 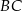 trójkąta prostokątnego
trójkąta prostokątnego 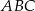 . Punkty
. Punkty 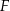 i
i 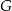 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 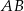 tak, że odcinki
tak, że odcinki 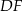 i
i 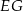 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 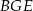 jest równe 1, a pole trójkąta
jest równe 1, a pole trójkąta 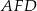 jest równe 4.
jest równe 4.
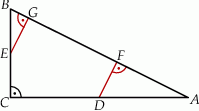
Zatem pole trójkąta 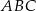 jest równe
jest równe
A) 12 B) 16 C) 18 D) 20
Na przyprostokątnych 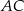 i
i 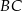 trójkąta prostokątnego
trójkąta prostokątnego 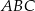 wybrano punkty
wybrano punkty 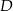 i
i 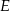 tak, że
tak, że 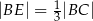 i
i 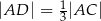 . Punkty
. Punkty 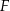 i
i 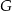 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 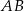 tak, że odcinki
tak, że odcinki 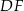 i
i 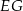 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 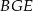 jest równe 1, a pole trójkąta
jest równe 1, a pole trójkąta 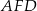 jest równe 4.
jest równe 4.
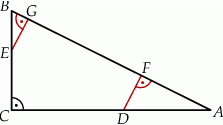
Zatem pole trójkąta  jest równe
jest równe
A) 40 B) 15 C) 45 D) 20
Na przyprostokątnych 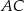 i
i 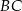 trójkąta prostokątnego
trójkąta prostokątnego 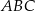 wybrano punkty
wybrano punkty 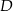 i
i 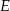 tak, że
tak, że 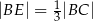 i
i 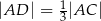 . Punkty
. Punkty 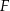 i
i 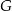 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 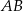 tak, że odcinki
tak, że odcinki 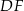 i
i 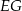 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 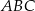 jest równe 36.
jest równe 36.
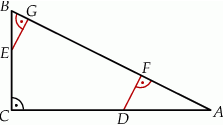
Zatem suma pól trójkątów 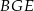 i
i 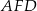 jest równa
jest równa
A) 4 B) 12 C) 18 D) 9
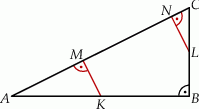
Punkty 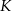 i
i 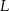 są środkami przyprostokątnych
są środkami przyprostokątnych 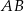 i
i 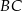 trójkąta prostokątnego
trójkąta prostokątnego 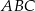 . Punkty
. Punkty 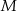 i
i 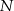 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 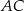 tak, że odcinki
tak, że odcinki 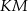 i
i 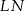 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 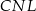 jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta 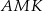 jest równe 5.
jest równe 5.
Zatem pole trójkąta 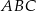 jest równe
jest równe
A) 32 B) 16 C) 28 D) 18
Przyprostokątne w trójkącie prostokątnym mają długości 1 i 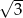 . Najmniejszy kąt w tym trójkącie ma miarę
. Najmniejszy kąt w tym trójkącie ma miarę
A) 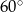 B)
B) 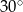 C)
C) 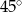 D)
D) 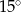
Przyprostokątne w trójkącie prostokątnym mają długości 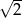 i
i 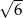 . Największy kąt ostry w tym trójkącie ma miarę
. Największy kąt ostry w tym trójkącie ma miarę
A) 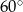 B)
B) 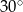 C)
C) 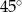 D)
D) 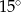
Dany jest trójkąt prostokątny (patrz rysunek).
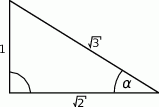
Wtedy 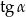 jest równy
jest równy
A) 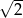 B)
B) 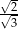 C)
C) 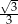 D)
D) 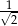
Dany jest trójkąt prostokątny (patrz rysunek).
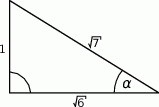
Wtedy 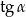 jest równy
jest równy
A) 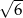 B)
B) 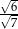 C)
C) 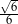 D)
D) 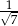
Dany jest trójkąt prostokątny (patrz rysunek).
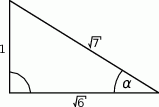
Wtedy 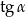 jest równy
jest równy
A) 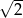 B)
B) 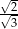 C)
C) 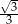 D)
D) 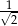
Dany jest trójkąt prostokątny (patrz rysunek).
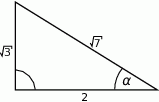
Wtedy 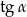 jest równy
jest równy
A) 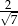 B)
B) 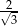 C)
C) 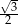 D)
D) 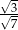
Dane są dwa trójkąty podobne 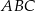 i
i 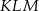 o polach równych – odpowiednio –
o polach równych – odpowiednio – 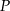 oraz
oraz 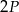 . Obwód trójkąta
. Obwód trójkąta 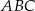 jest równy
jest równy  . Obwód trójkąta
. Obwód trójkąta 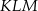 jest równy
jest równy
A) 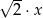 , , | B) 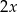 , , |
| ponieważ stosunek obwodów trójkątów podobnych jest równy | |
| 1) | kwadratowi stosunku pól tych trójkątów. |
| 2) | pierwiastkowi kwadratowemu ze stosunku pól tych trójkątów. |
| 3) | stosunkowi pól tych trójkątów. |
Dane są dwa trójkąty podobne 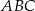 i
i 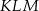 o polach równych – odpowiednio –
o polach równych – odpowiednio – 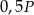 oraz
oraz 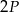 . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 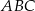 jest równy
jest równy  . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 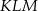 jest równy
jest równy
A) 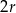 , , | B) 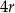 , , |
| ponieważ stosunek promieni okręgów wpisanych trójkątów podobnych jest równy | |
| 1) | pierwiastkowi kwadratowemu ze stosunku pól tych trójkątów. |
| 2) | kwadratowi stosunku pól tych trójkątów. |
| 3) | stosunkowi pól tych trójkątów. |
Długość odcinka zaznaczonego na rysunku literką  jest równa
jest równa
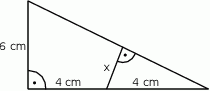
A) 2,4 cm B) 3 cm C) 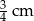 D) 2 cm
D) 2 cm
Środkowe w trójkącie 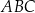 przecinają się w punkcie
przecinają się w punkcie 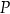 odległym od wierzchołka
odległym od wierzchołka 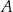 o 6 cm. Wobec tego środkowa poprowadzona na bok
o 6 cm. Wobec tego środkowa poprowadzona na bok 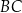 ma długość
ma długość
A) 12 cm B) 9 cm C) 15 cm D) 10 cm
Punkt 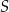 jest środkiem ciężkości trójkąta
jest środkiem ciężkości trójkąta 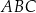 . Długość odcinka
. Długość odcinka 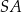 jest równa 10. Długość środkowej poprowadzonej z wierzchołka
jest równa 10. Długość środkowej poprowadzonej z wierzchołka 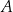 do boku
do boku 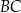 jest równa
jest równa
A) 10 B) 15 C) 20 D) 30
Środkowe w trójkącie 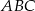 przecinają się w punkcie
przecinają się w punkcie 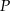 , przy czym długość środkowej opuszczonej na bok
, przy czym długość środkowej opuszczonej na bok 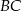 ma długość 9 cm. Wobec tego długość odcinka
ma długość 9 cm. Wobec tego długość odcinka 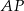 wynosi
wynosi
A) 6 cm B) 3 cm C) 2 cm D) 5 cm
Środkowe w trójkącie 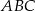 przecinają się w punkcie
przecinają się w punkcie 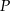 odległym od wierzchołka
odległym od wierzchołka 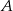 o 6 cm. Środkowa opuszczona na bok
o 6 cm. Środkowa opuszczona na bok 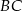 przecina ten bok w punkcie
przecina ten bok w punkcie 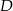 . Wobec tego długość odcinka
. Wobec tego długość odcinka 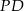 wynosi
wynosi
A) 1 cm B) 2 cm C) 3 cm D) 6 cm
Jeżeli  i
i 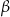 są miarami kątów ostrych trójkąta prostokątnego oraz
są miarami kątów ostrych trójkąta prostokątnego oraz 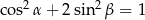 to
to
A) 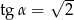 B)
B) 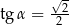 C)
C) 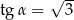 D)
D) 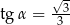
Jeżeli  i
i 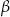 są miarami kątów ostrych trójkąta prostokątnego oraz
są miarami kątów ostrych trójkąta prostokątnego oraz 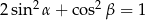 to
to
A) 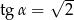 B)
B) 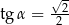 C)
C) 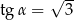 D)
D) 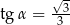
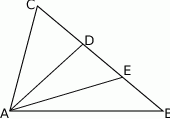
Punkty 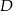 i
i 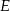 dzielą bok
dzielą bok 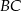 trójkąta
trójkąta 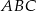 na trzy równe części (zobacz rysunek). Stosunek pól trójkątów
na trzy równe części (zobacz rysunek). Stosunek pól trójkątów 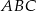 i
i 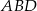 jest równy
jest równy
A)  B)
B)  C)
C)  D)
D) 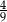
Dany jest równoramienny trójkąt 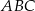 o kącie przy podstawie
o kącie przy podstawie 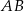 równym
równym 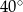 . Punkt
. Punkt 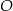 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 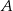 i
i 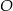 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 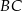 w punkcie
w punkcie 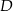 . Jeśli miara kąta
. Jeśli miara kąta 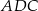 jest równa
jest równa  , to
, to
A) 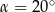 B)
B) 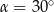 C)
C) 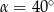 D)
D) 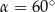
Dany jest równoramienny trójkąt 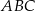 o kącie przy podstawie
o kącie przy podstawie 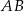 równym
równym 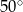 . Punkt
. Punkt 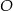 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 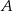 i
i 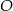 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 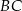 w punkcie
w punkcie 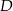 . Jeśli miara kąta
. Jeśli miara kąta 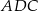 jest równa
jest równa  , to
, to
A) 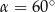 B)
B) 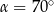 C)
C) 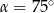 D)
D) 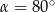
Dany jest równoramienny trójkąt 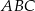 o kącie przy podstawie
o kącie przy podstawie 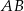 równym
równym 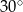 . Punkt
. Punkt 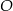 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 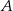 i
i 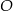 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 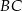 w punkcie
w punkcie 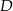 . Jeśli miara kąta
. Jeśli miara kąta 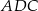 jest równa
jest równa  , to
, to
A) 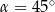 B)
B) 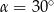 C)
C) 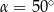 D)
D) 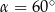
Odcinek 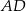 jest dwusieczną w trójkącie równoramiennym
jest dwusieczną w trójkącie równoramiennym 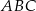 poprowadzoną do ramienia
poprowadzoną do ramienia 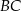 .
.
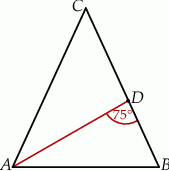
Jeżeli 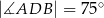 to miara kąta przy wierzchołku
to miara kąta przy wierzchołku 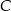 jest równa
jest równa
A) 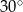 B)
B) 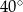 C)
C) 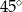 D)
D) 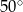
Okrąg jest styczny do boku 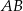 trójkąta
trójkąta 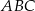 w punkcie
w punkcie 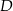 oraz przecina boki
oraz przecina boki 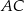 i
i 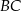 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 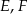 i
i 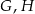 (zobacz rysunek). Kat
(zobacz rysunek). Kat 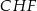 ma miarę
ma miarę 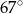 .
.
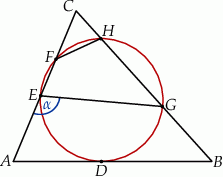
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 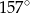 B)
B) 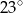 C)
C) 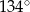 D)
D) 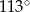
Okrąg jest styczny do boku 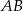 trójkąta
trójkąta 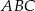 w punkcie
w punkcie 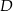 oraz przecina boki
oraz przecina boki 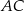 i
i 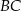 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 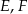 i
i 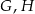 (zobacz rysunek). Kat
(zobacz rysunek). Kat 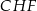 ma miarę
ma miarę 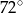 .
.
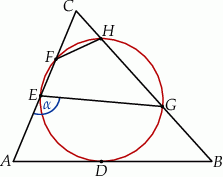
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 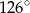 B)
B) 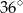 C)
C) 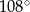 D)
D) 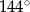
Obwód trójkąta prostokątnego równoramiennego wynosi 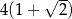 . Długość wysokości poprowadzonej z wierzchołka kąta prostego tego trójkąta jest równa
. Długość wysokości poprowadzonej z wierzchołka kąta prostego tego trójkąta jest równa
A) 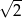 B) 4 C) 2 D)
B) 4 C) 2 D) 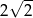
W trójkącie równoramiennym 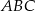 dane są
dane są 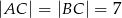 oraz
oraz 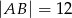 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 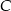 jest równa
jest równa
A) 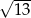 B)
B) 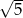 C) 1 D) 5
C) 1 D) 5
Podstawa trójkąta równoramiennego ma długość 6, a ramię ma długość 5. Wysokość opuszczona na podstawę ma długość
A) 3 B) 4 C) 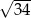 D)
D) 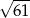
W trójkącie równoramiennym 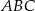 dane są
dane są 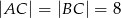 oraz
oraz 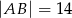 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 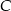 jest równa
jest równa
A) 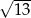 B)
B) 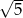 C)
C) 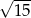 D)
D) 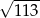
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 7. Wysokość opuszczona na podstawę ma długość
A) 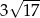 B)
B) 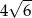 C)
C) 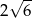 D)
D) 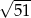
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 13. Wysokość opuszczona na podstawę ma długość
A) 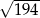 B)
B) 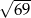 C) 12 D) 11
C) 12 D) 11
W trójkącie równoramiennym 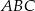 dane są
dane są 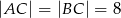 oraz
oraz 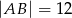 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 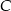 jest równa
jest równa
A) 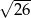 B)
B) 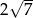 C) 2 D)
C) 2 D) 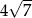
W trójkącie równoramiennym 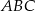 dane są
dane są 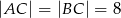 oraz
oraz 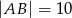 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 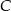 jest równa
jest równa
A) 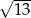 B)
B) 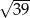 C) 6 D)
C) 6 D) 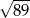
Połączono środki boków trójkąta 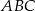 otrzymując trójkąt
otrzymując trójkąt 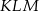 . O ile procent pole trójkąta
. O ile procent pole trójkąta 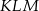 jest mniejsze od pola trójkąta
jest mniejsze od pola trójkąta 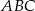 ?
?
A) 80% B) 75% C) 50% D) 25%
Promień okręgu wpisanego w trójkąt równoboczny jest o 2 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 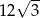 B)
B) 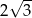 C)
C)  D)
D) 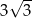
Promień okręgu wpisanego w trójkąt równoboczny jest o 1 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 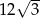 B)
B) 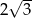 C)
C) 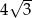 D)
D) 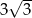
Promień okręgu wpisanego w trójkąt równoboczny jest o 1 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 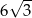 B)
B) 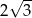 C)
C) 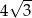 D)
D) 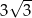
Długość boku trójkąta równobocznego wynosi 12. Pole koła wpisanego w ten trójkąt jest równe
A) 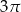 B)
B) 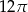 C)
C) 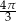 D)
D) 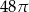
Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku 1:4, mogą być równe
A) 9 i 36 B) 18 i 36 C) 9 i 144 D) 18 i 144
