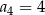Miary kątów trójkąta tworzą ciąg arytmetyczny o pierwszym wyrazie 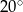 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 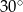 B)
B) 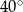 C)
C) 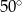 D)
D) 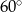
/Szkoła średnia/Zadania testowe/Ciągi/Arytmetyczny
Miary kątów trójkąta tworzą ciąg arytmetyczny o pierwszym wyrazie 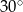 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 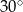 B)
B) 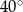 C)
C) 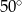 D)
D) 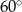
Miary kątów trójkąta tworzą ciąg arytmetyczny o pierwszym wyrazie 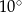 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 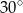 B)
B) 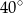 C)
C) 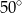 D)
D) 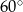
Ciąg 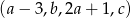 jest arytmetyczny i suma trzech jego początkowych wyrazów jest równa 78. Liczba
jest arytmetyczny i suma trzech jego początkowych wyrazów jest równa 78. Liczba  jest równa
jest równa
A) 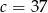 B)
B)  C)
C) 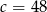 D)
D) 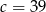
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 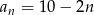 , gdzie
, gdzie 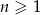 jest równa 14. Zatem
jest równa 14. Zatem
A) 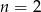 B) liczba
B) liczba 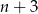 dzieli się przez 5 C)
dzieli się przez 5 C) 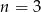 D)
D) 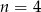
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 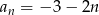 , gdzie
, gdzie 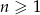 jest równa
jest równa 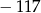 . Zatem
. Zatem
A) 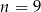 B)
B) 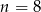 C)
C) 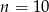 D)
D) 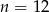
Suma dwóch początkowych wyrazów ciągu arytmetycznego 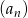 wynosi 5, a trzeci wyraz jest równy 7. Wówczas
wynosi 5, a trzeci wyraz jest równy 7. Wówczas
A) 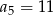 B)
B) 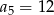 C)
C) 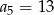 D)
D) 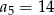
Suma dwóch początkowych wyrazów ciągu arytmetycznego 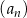 wynosi 7, a trzeci wyraz jest równy 5. Wówczas
wynosi 7, a trzeci wyraz jest równy 5. Wówczas
A) 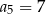 B)
B) 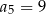 C)
C) 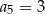 D)
D) 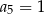
Suma ciągu arytmetycznego jest określona wzorem 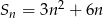 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 24 B) 15 C) 6 D) 2
Suma częściowa ciągu arytmetycznego jest wyrażona wzorem 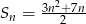 . Wobec tego:
. Wobec tego:
A) 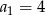 B)
B) 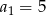 C)
C) 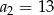 D)
D) 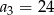
Suma ciągu arytmetycznego jest określona wzorem 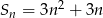 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 18 B) 3 C) 12 D) 15
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 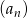 wyraża się wzorem
wyraża się wzorem 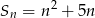 (
(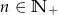 ). Drugi wyraz ciągu
). Drugi wyraz ciągu 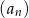 jest równy
jest równy
A) 2 B) 8 C) 12 D) 14
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 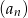 jest określona wzorem
jest określona wzorem 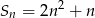 . Wtedy wyraz
. Wtedy wyraz 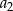 jest równy
jest równy
A) 3 B) 6 C) 7 D) 10
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 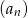 jest określona wzorem
jest określona wzorem 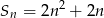 . Wtedy wyraz
. Wtedy wyraz 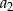 jest równy
jest równy
A) 4 B) 8 C) 12 D) 24
Jeśli suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 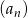 określona jest wzorem
określona jest wzorem 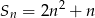 , to wartość trzeciego wyrazu tego ciągu jest równa
, to wartość trzeciego wyrazu tego ciągu jest równa
A) 8 B) 10 C) 11 D) 21
Suma ciągu arytmetycznego jest określona wzorem 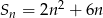 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 20 B) 16 C) 12 D) 8
Jeżeli suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 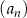 określona jest wzorem
określona jest wzorem 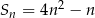 , to wartość piątego wyrazu tego ciągu jest równa
, to wartość piątego wyrazu tego ciągu jest równa
A) 33 B) 35 C) 60 D) 95
Ciąg arytmetyczny 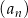 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 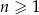 . Różnica tego ciągu jest równa 2. Wtedy
. Różnica tego ciągu jest równa 2. Wtedy
A) 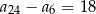 B)
B) 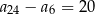 C)
C) 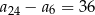 D)
D) 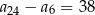
Ciąg arytmetyczny 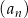 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 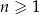 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa 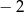 . Wtedy
. Wtedy
A) 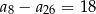 B)
B) 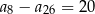 C)
C) 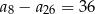 D)
D) 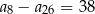
W ciągu arytmetycznym 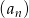 , określonym dla
, określonym dla 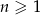 , dane są dwa wyrazy:
, dane są dwa wyrazy: 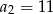 i
i 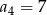 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 36 B) 40 C) 13 D) 20
W ciągu arytmetycznym 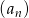 , określonym dla
, określonym dla 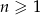 , dane są dwa wyrazy:
, dane są dwa wyrazy: 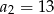 i
i 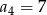 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 92 B) 39 C) 46 D) 50
W ciągu arytmetycznym 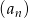 dane są
dane są 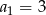 i
i 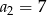 . Wtedy suma
. Wtedy suma 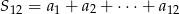 jest równa
jest równa
A) 324 B) 300 C) 282 D) 306
Suma dwudziestu początkowych wyrazów nieskończonego ciągu arytmetycznego 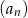 , w którym
, w którym 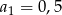 oraz
oraz 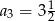 jest równa
jest równa
A) 295 B) 298 C) 305 D) 308
Suma  początkowych wyrazów ciągu arytmetycznego wyraża się wzorem
początkowych wyrazów ciągu arytmetycznego wyraża się wzorem 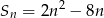 . Wynika stąd, że różnica ciągu jest równa
. Wynika stąd, że różnica ciągu jest równa
A) -8 B) 4 C) 6 D) 8
Suma  początkowych wyrazów ciągu arytmetycznego wyraża się wzorem
początkowych wyrazów ciągu arytmetycznego wyraża się wzorem 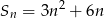 . Wynika stąd, że różnica ciągu jest równa
. Wynika stąd, że różnica ciągu jest równa
A) -6 B) 14 C) 6 D) 8
Suma  początkowych wyrazów ciągu arytmetycznego wyraża się wzorem
początkowych wyrazów ciągu arytmetycznego wyraża się wzorem 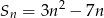 . Wynika stąd, że różnica ciągu jest równa
. Wynika stąd, że różnica ciągu jest równa
A) -8 B) 4 C) 6 D) 8
Suma  początkowych wyrazów ciągu arytmetycznego, gdzie
początkowych wyrazów ciągu arytmetycznego, gdzie 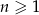 , wyraża się wzorem
, wyraża się wzorem 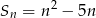 . Wobec tego różnica tego ciągu wynosi
. Wobec tego różnica tego ciągu wynosi
A) -5 B) -3 C) 1 D) 2
Suma  początkowych wyrazów ciągu arytmetycznego, gdzie
początkowych wyrazów ciągu arytmetycznego, gdzie 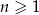 , wyraża się wzorem
, wyraża się wzorem 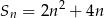 . Wobec tego różnica tego ciągu wynosi
. Wobec tego różnica tego ciągu wynosi
A) 4 B) 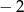 C)
C) 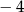 D) 2
D) 2
Suma  początkowych wyrazów ciągu arytmetycznego, gdzie
początkowych wyrazów ciągu arytmetycznego, gdzie 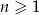 , wyraża się wzorem
, wyraża się wzorem 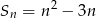 . Wobec tego różnica tego ciągu wynosi
. Wobec tego różnica tego ciągu wynosi
A) 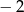 B)
B) 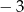 C) 2 D) 1
C) 2 D) 1
Pierwszy wyraz ciągu arytmetycznego jest równy 5, a różnica tego ciągu jest równa 3. Suma 100 początkowych wyrazów tego ciągu o numerach parzystych jest równa
A) 15100 B) 30500 C) 30200 D) 61000
Suma trzydziestu początkowych wyrazów ciągu arytmetycznego 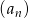 danego wzorem
danego wzorem 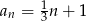 jest równa
jest równa
A) 370 B) 185 C) 11 D) 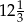
Ciąg arytmetyczny 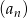 jest określony wzorem
jest określony wzorem 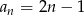 , dla
, dla 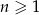 . Suma stu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma stu początkowych kolejnych wyrazów tego ciągu jest równa
A) 9900 B) 9950 C) 10000 D) 10050
Suma dwudziestu początkowych wyrazów ciągu arytmetycznego 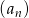 danego wzorem
danego wzorem 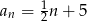 jest równa
jest równa
A) 205 B) 410 C) 200 D) 210
Suma dwudziestu początkowych wyrazów nieskończonego ciągu arytmetycznego 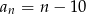 wynosi
wynosi
A) 8 B) 9 C) 10 D) 11
Suma dwudziestu początkowych wyrazów ciągu arytmetycznego 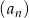 danego wzorem
danego wzorem 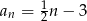 jest równa
jest równa
A) 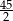 B)
B) 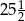 C) 45 D)
C) 45 D) 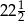
Suma dziesięciu początkowych wyrazów nieskończonego ciągu arytmetycznego 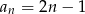 wynosi
wynosi
A) 80 B) 90 C) 110 D) 100
Wszystkie dwucyfrowe liczby naturalne podzielne przez 7 tworzą rosnący ciąg arytmetyczny. Dwunastym wyrazem tego ciągu jest liczba
A) 77 B) 84 C) 91 D) 98
Wszystkie dwucyfrowe liczby naturalne podzielne przez 8 tworzą rosnący ciąg arytmetyczny. Jedenastym wyrazem tego ciągu jest liczba
A) 92 B) 72 C) 88 D) 96
Dany jest ciąg arytmetyczny o pierwszym wyrazie 6 i różnicy 2. Wyraz ogólny ciągu wyraża się wzorem
A) 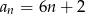 B)
B) 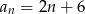 C)
C) 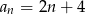 D)
D) 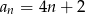
Dany jest ciąg arytmetyczny o pierwszym wyrazie 7 i różnicy 3. Wyraz ogólny ciągu wyraża się wzorem
A) 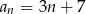 B)
B) 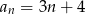 C)
C) 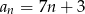 D)
D) 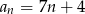
Dany jest ciąg arytmetyczny o pierwszym wyrazie 8 i różnicy 6. Wyraz ogólny ciągu wyraża się wzorem
A) 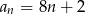 B)
B) 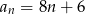 C)
C) 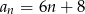 D)
D) 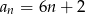
Suma kwadratów trzech początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie 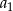 i różnicy
i różnicy  wyraża się wzorem
wyraża się wzorem
A) 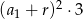 B)
B) 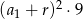 C)
C) 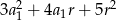 D)
D) 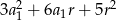
Suma kwadratów czterech początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie 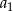 i różnicy
i różnicy  wyraża się wzorem
wyraża się wzorem
A) 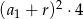 B)
B) 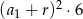 C)
C) 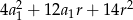 D)
D) 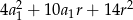
Wzór ogólny ciągu arytmetycznego, w którym 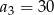 i
i 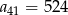 , to
, to
A) 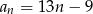 B)
B) 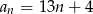 C)
C) 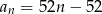 D)
D) 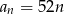
W ciągu arytmetycznym 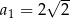 i
i 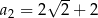 . Suma wyrazów od dziesiątego do czterdziestego włącznie jest równa
. Suma wyrazów od dziesiątego do czterdziestego włącznie jest równa
A) 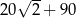 B)
B) 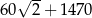 C)
C) 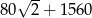 D)
D) 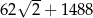
Ciąg arytmetyczny 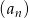 określony jest wzorem
określony jest wzorem 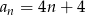 . Zatem suma
. Zatem suma 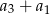 jest równa
jest równa
A) 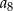 B)
B) 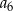 C)
C) 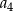 D)
D) 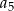
Ciąg arytmetyczny 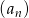 określony jest wzorem
określony jest wzorem 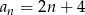 . Zatem suma
. Zatem suma 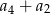 jest równa
jest równa
A) 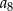 B)
B) 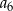 C)
C) 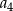 D)
D) 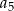
Ciąg arytmetyczny 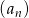 określony jest wzorem
określony jest wzorem 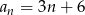 . Zatem suma
. Zatem suma 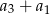 jest równa
jest równa
A) 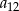 B)
B) 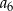 C)
C) 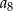 D)
D) 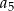
Ciągi 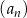 ,
, 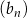 oraz
oraz 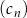 są określone dla każdej liczby naturalnej
są określone dla każdej liczby naturalnej 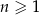 następująco:
następująco:
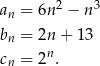
Wskaż zdanie prawdziwe.
A) Ciąg 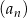 jest arytmetyczny.
jest arytmetyczny.
B) Ciąg 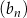 jest arytmetyczny.
jest arytmetyczny.
C) Ciąg 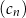 jest arytmetyczny.
jest arytmetyczny.
D) Wśród ciągów 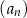 ,
, 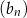 ,
, 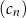 nie ma ciągu arytmetycznego.
nie ma ciągu arytmetycznego.
Ciągi 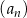 ,
, 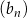 oraz
oraz 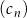 są określone dla każdej liczby naturalnej
są określone dla każdej liczby naturalnej 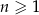 następująco:
następująco:
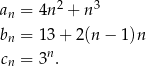
Wskaż zdanie prawdziwe.
A) Ciąg 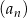 jest arytmetyczny.
jest arytmetyczny.
B) Ciąg 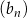 jest arytmetyczny.
jest arytmetyczny.
C) Ciąg 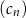 jest arytmetyczny.
jest arytmetyczny.
D) Wśród ciągów 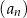 ,
, 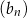 ,
, 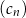 nie ma ciągu arytmetycznego.
nie ma ciągu arytmetycznego.
Dwa kolejne wyrazy ciągu arytmetycznego są równe 79 i 75. Wyrazem tego ciągu może być liczba
A) 2015 B) 2016 C) 2017 D) 2018
W ciągu arytmetycznym mamy 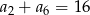 . Oblicz
. Oblicz 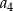 .
.
A) 8 B) 16 C) 4 D) 12
Ciąg arytmetyczny 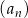 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 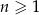 . Trzeci i piąty wyraz ciągu spełniają warunek
. Trzeci i piąty wyraz ciągu spełniają warunek 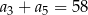 . Wtedy czwarty wyraz tego ciągu jest równy
. Wtedy czwarty wyraz tego ciągu jest równy
A) 28 B) 29 C) 33 D) 40
Dla ciągu arytmetycznego 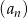 , określonego dla
, określonego dla 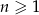 , spełniony jest warunek
, spełniony jest warunek 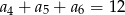 . Wtedy
. Wtedy
A) 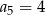 B)
B) 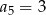 C)
C) 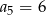 D)
D) 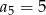
W ciągu arytmetycznym 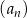 , określonym dla
, określonym dla 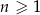 , spełniony jest warunek
, spełniony jest warunek 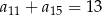 . Wtedy
. Wtedy
A) 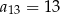 B)
B) 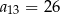 C)
C) 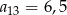 D)
D) 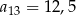
Ciąg arytmetyczny 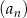 , określony dla
, określony dla 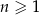 , spełnia warunek
, spełnia warunek 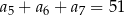 . Wtedy
. Wtedy
A) 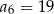 B)
B) 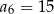 C)
C) 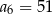 D)
D) 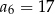
Ciąg arytmetyczny 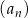 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 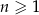 . Trzeci i piąty wyraz ciągu spełniają warunek
. Trzeci i piąty wyraz ciągu spełniają warunek 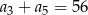 . Wtedy czwarty wyraz tego ciągu jest równy
. Wtedy czwarty wyraz tego ciągu jest równy
A) 28 B) 29 C) 33 D) 40
Ciąg arytmetyczny 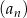 , określony dla
, określony dla 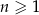 , spełnia warunek
, spełnia warunek 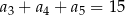 . Wtedy
. Wtedy
A) 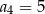 B)
B) 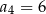 C)
C) 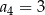 D)
D)